Косоугольная диметрическая проекция (фронтальная)

Если расположить координатные оси Х и Y параллельно плоскости П¢, то показатели искажения по этим осям станут равным единице (к = т =1). Показатель искажения по оси Y обычно принимают равным 0,5. Аксонометрические оси X' и Z' составят прямой угол, ось Y' обычно проводят как биссектрису этого угла. Ось Х может быть направлена как вправо от оси Z', так и влево.

Предпочтительно пользоваться правой системой, так как удобнее изображать предметы в рассеченном виде. В этом виде аксонометрии хорошо чертить детали, имеющие форму цилиндра или конуса.

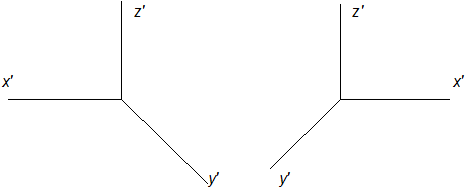
Рис. 10.20

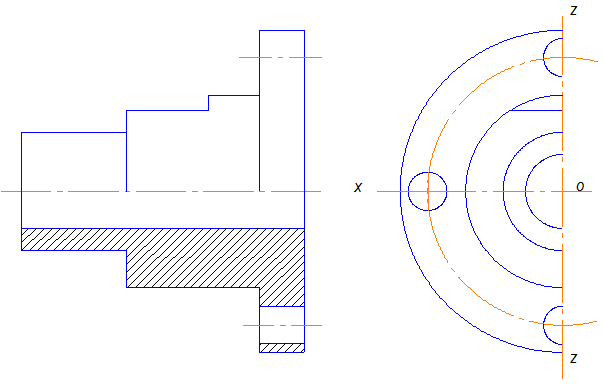
Рис.10.21

Для удобства изображения этой детали ось Y надо совместить с осью вращения поверхностей цилиндров. Тогда все окружности будут изображаться в натуральную величину, а длина каждой поверхности будет уменьшаться в два раза (рис.10.21).

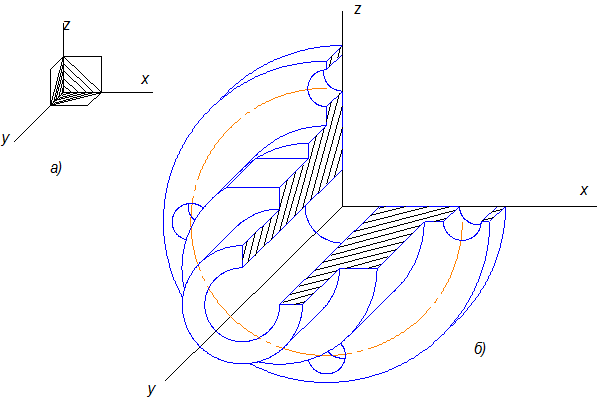
Рис. 10.22

Наклонные сечения.

При выполнении чертежей деталей машин приходится нередко применять наклонные сечения.

При решении таких задач необходимо прежде всего уяснить: как должна быть расположена секущая плоскость и какие поверхности участвуют в сечении для того, чтобы деталь читалась лучше. Рассмотрим примеры.

Дана четырехгранная пирамида, которая рассекается наклонной фронтально-проецирующей плоскостью А-А (рис.11.1). Сечением будет четырехугольник.

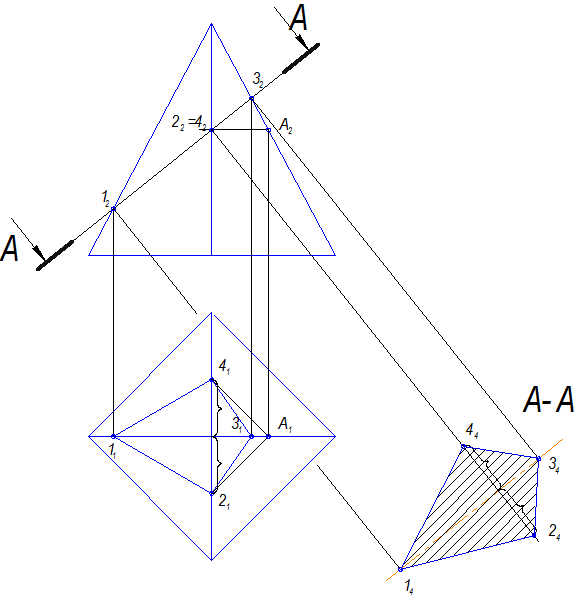
Рис. 11.1

Сначала строим проекции его на П₁ и на П₂ . Фронтальная проекция совпадает с проекцией плоскости, а горизонтальную проекцию четырехугольника строим по принадлежности пирамиде.

Затем строим натуральную величину сечения. Для этого вводится дополнительная плоскость проекций П₄ , параллельная заданной секущей плоскости А-А, на нее проецируем четырехугольник, а затем совмещаем его с плоскостью чертежа.

Эта четвертая основная задача преобразования комплексного чертежа (модуль №4, стр.15 или задача №117 из рабочей тетради по начертательной геометрии).

Построения выполняются в следующей последовательности (рис.11.2):

1. 1.На свободном месте чертежа проводим осевую линию, параллельную плоскости А-А.

2. 2.Из точек пересечения ребер пирамиды с плоскостью проводим проецирующие лучи, перпендикулярно секущей плоскости. Точки 1 и 3 будут лежать на линии, расположенной перпендикулярно осевой.

3. 3.Расстояние между точками 2 и 4 переносится с горизонтальной проекции.

4. Аналогично строится истинная величина сечения поверхности вращения - эллипс.

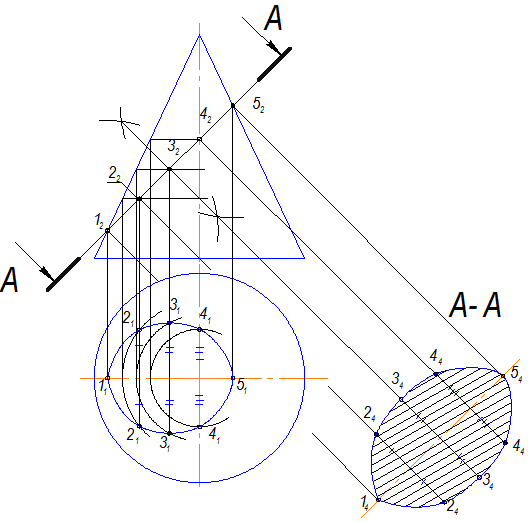
Рис. 11.2

Расстояние между точками 1 и 5 -большая ось эллипса. Малую ось эллипса надо строить путем деления большой оси пополам (3-3).

Расстояние между точками 2-2, 3-3, 4-4 переносятся с горизонтальной проекции.

Рассмотрим более сложный пример, включающий многогранные поверхности и поверхности вращения (рис.11.3)

Задана четырехгранная призма. В ней расположены два отверстия: призматическое, расположенное горизонтально и цилиндрическое, ось которого совпадает с высотой призмы.

Секущая плоскость фронтально-проецирующая, поэтому фронтальная проекция сечения совпадает с проекцией этой плоскости.

Четырехугольная призма проецирующая к горизонтальной плоскости проекций, а значит и горизонтальная проекция сечения тоже есть на чертеже, она совпадает с горизонтальной проекцией призмы.

Натуральная величина сечения, в которое попадают обе призмы и цилиндр, строим на плоскости, параллельной секущей плоскости А-А (рис.11.3).

Последовательность выполнения наклонного сечения:

1. Проводится ось сечения, параллельно секущей плоскости, на свободном поле чертежа.

2. Строится сечение наружной призмы: длина его переносится с фронтальной проекции, а расстояние между точками с горизонтальной.

3. Строится сечение цилиндра - часть эллипса. Сначала строятся характерные точки, определяющие длину малой и большой оси (5₄, 2₄ -2₄ ) и точки, ограничивающие эллипс (1₄ -1₄ ), затем дополнительные точки (4₄ -4₄ и 3₄ -3₄ ).

4. Строится сечение призматического отверстия.

5. Наносится штриховка под углом 45° к основной надписи, если она не совпадает с линиями контура, а если совпадает, то угол штриховки может быть 30° или 60°. Плотность штриховки на сечении такая же, как на ортогональном чертеже.

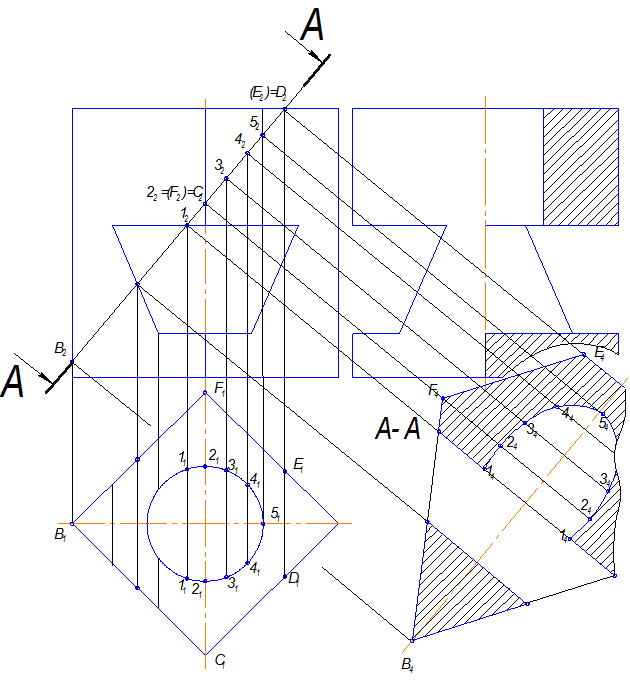
Рис.11.3

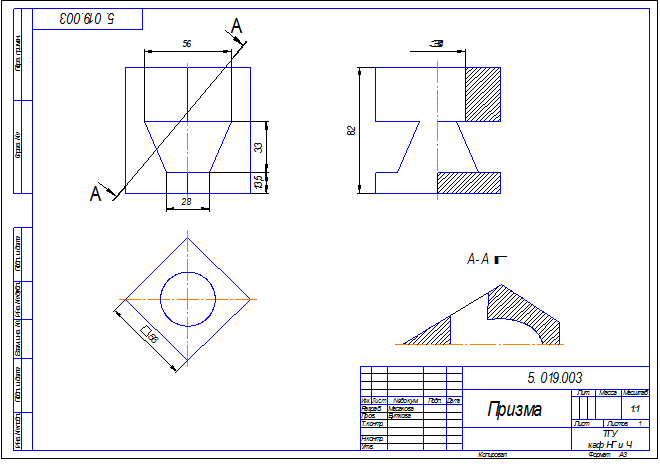
Рис.11.4

Наклонное сечение можно поворачивать. При этом обозначение сопровождается знаком 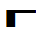. Также разрешается показать половину фигуры наклонного сечения, если она симметрична. Подобное расположение наклонного сечения показано на рис.13.4. Обозначения точек при построении наклонного сечения можно не ставить.

На рис.11.5 дано наглядное изображение заданной фигуры с сечением плоскостью А-А.

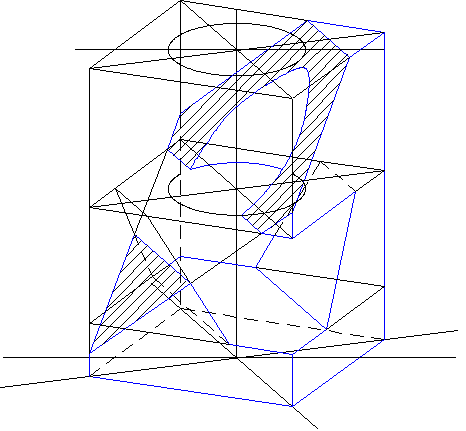
Рис. 11.5