Краткие теоретические сведения об аксонометрических проекциях

Комплексный чертеж, составленный из двух или трех проекций, обладая свойствами обратимости, простоты и др., вместе с тем имеет существенный недостаток: ему недостает наглядности. Поэтому, желая дать более наглядное представление о предмете, наряду с комплексным чертежом приводят аксонометрический, широко используемый при описании конструкций изделий, в руководствах по эксплуатации, в схемах сборки, для пояснений чертежей машин, механизмов и их деталей.

Сравните два изображения - ортогональный чертеж и аксонометрический одной и той же модели. На каком изображении легче прочитать форму? Конечно на аксонометрическом изображении. (рис.10.1)

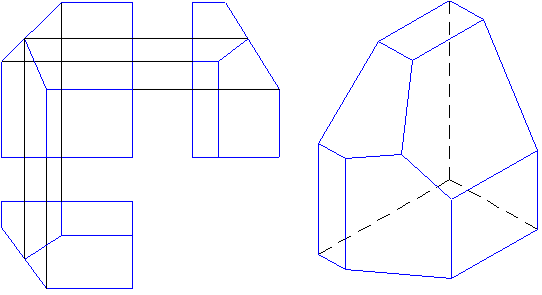
Рис.10.1

Сущность аксонометрического проецирования состоит в том, что геометрическая фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, параллельно проецируется на некоторую плоскость проекций, называемую аксонометрическая плоскость проекций, или картинная плоскость.

Если отложить на осях координат x,y и z отрезок l (lx,ly,lz) и спроецировать на плоскость П¢ , то получим аксонометрические оси и на них отрезки l'x, l'y, l'z (рис.10.2)

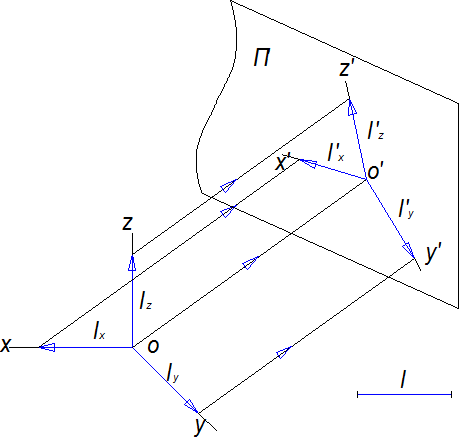
Рис.10.2

lx, ly, lz- натуральные масштабы.

l = lx = ly = lz

l'x, l'y, l'z - аксонометрические масштабы.

Полученную совокупность проекций на П¢ называют аксонометрией.

Отношение длины аксонометрических масштабных отрезков к длине натуральных масштабных отрезков называют показателем или коэффициентом искажения по осям, которые обозначаются Кx, Ky, Kz.

Kx = ;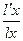

Ky= ;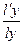

Kz=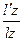

Виды аксонометрических изображений зависят:

1. От направления проецирующих лучей (они могут быть перпендикулярны П' - тогда аксонометрия будет называться ортогональной (прямоугольной) или расположены под углом не равным 90°- косоугольная аксонометрия).

2. От положения осей координат к аксонометрической плоскости.

Здесь возможны три случая: когда все три оси координат составляют с аксонометрической плоскостью проекций некоторые острые углы (равные и неравные) и когда одна или две оси ей параллельны.

В первом случае применяется только прямоугольное проецирование, (s ^ П') во втором и третьем - только косоугольное проецирование (s 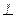П').

Если оси координат ОХ, ОY,OZ не параллельны аксонометрической плоскости проекций П', то будут ли они проецироваться на нее в натуральную величину? Конечно, нет. Изображение прямых в общем случае всегда меньше натуральной величины.

Рассмотрим ортогональный чертеж точки А и ее аксонометрическое изображение.

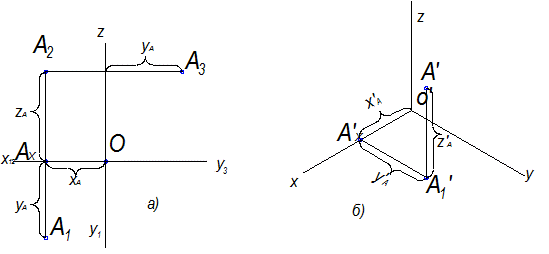
Рис.10.3

Положение точки определяют три координаты – Х_А, Y_А, Z_A, полученные путем измерения звеньев натуральной ломаной ОА_Х - А_ХА₁ – А₁ А (рис.10.3).

A'- главная аксонометрическая проекция точки А;

А - вторичная проекция точки А (проекция проекции точки).

Коэффициентами искажения по осям Х', Y' и Z' будут:

k_x = 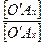; k_y = 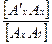; k_y =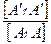

В ортогональной аксонометрии эти показатели равны косинусам углов наклона осей координат к аксонометрической плоскости, а следовательно, они всегда меньше единицы.

Их связывает формула

k²_x + k² _y + k² _z = 2 (I)

В косоугольной аксонометрии показатели искажения связаны формулой

k_x + k_y + k_z = 2+ctg a (III)

т.е. любой из них может быть меньше, равен или больше единицы (здесь a- угол наклона проецирующих лучей к аксонометрической плоскости). Обе формулы - вывод из теоремы Польке.

Теорема Польке: аксонометрические оси на плоскости чертежа (П¢) и масштабы на них могут быть выбраны совершенно произвольно.

(Следовательно, аксонометрическая система (О' X' Y' Z') в общем случае определяется пятью независимыми параметрами: тремя аксонометрическими масштабами и двумя углами между аксонометрическими осями).

Углы наклона натуральных осей координат к аксонометрической плоскости проекций и направление проецирования могут быть выбраны произвольно, следовательно возможно множество видов ортогональных и косоугольных аксонометрий.

Их разделяют на три группы:

1. Все три показателя искажения равны (k_x = k_y = k_z). Этот вид аксонометрии называют изометрией. 3k²=2; k= 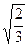» 0,82 - теоретический коэффициент искажения. Согласно ГОСТ 2.317-70 можно пользоваться К=1 - приведенный коэффициент искажения.

2. Два каких-либо показателя равны (например, kx=ky kz). Этот вид аксонометрии называется диметрией. k_x = k_z; k_y = 1/2k_x²; k_x² +k_z² + k_y²/4 = 2; k = 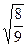» 0,94; k_x = 0,94; ky = 0,47; kz = 0,94 - теоретические коэффициенты искажения. Согласно ГОСТ 2.317-70 коэффициенты искажения могут быть приведенными - k_x=1; k_y=0,5; k_z=1.

3. 3. Все три показателя различны (k_x ¹ k_y ¹ k_z). Этот вид аксонометрии называют триметрией.

На практике применяют несколько видов как прямоугольной, так и косоугольной аксонометрии с наиболее простыми соотношениями между показателями искажений.