Особые линии плоскости.

Если прямая принадлежит плоскости и занимает в ней какое-то особое положение, то она называется особой линией плоскости. К ним относятся линии уровня плоскости: горизонталь, фронталь и профильная прямая, а также линии наибольшего наклона плоскости.

Горизонталь плоскости

Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций

Г (a || b) Построить: h Ì Г; h || П₁

1. Проводим h₂ перпендикулярно линиям связи.

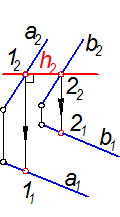
Рис. 2-11а

1. Так как h принадлежит плоскости, то h₁ находим по двум точкам в плоскости (1Î а, 2Î b). h₁ -натуральная величина h.

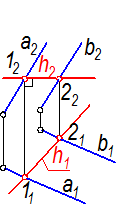
Рис. 2-11б

Построение горизонталив плоскости начинают с фронтальной проекции h₂: она всегда перпендикулярна линиям связи в системе П₂ –П₁. h₁ находят по принадлежности плоскости.

Если плоскость - фронтально проецирующая, то горизонталь такой плоскости – фронтально проецирующая прямая (рис. 2-12).

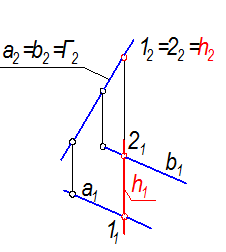
Рис. 2-12

Г(a || b) ^^ П₂; hÌ Г; h || П₁

Так как плоскость Г - фронтально проецирующая, то единственная прямая в такой плоскости, параллельная плоскости проекций П₁ - фронтально проецирующая прямая Þ h ^^ П₂

Фронталь плоскости

Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций

S (m Ç n) Построить: f Ì S; f || П₂

1. Проводим f₁ перпендикулярно линиям связи.

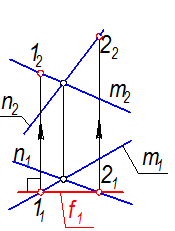
Рис. 2-13а

2. Так как f принадлежит плоскости, то f₂ находим по двум точкам в плоскости (1Î m, 2Î n).

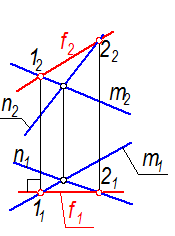
Рис. 2-13б

Построение фронтали в плоскости начинают с горизонтальной проекции f₁ : она всегда перпендикулярна линиям связи в системе П₂ –П₁. f₂ находят по принадлежности плоскости.

Это - натуральная величина f.

Если плоскость - горизонтально проецирующая, то фронталь такой плоскости - горизонтально проецирующая прямая (рис. 2-14).

S(m Ç n) ^^ П₁; f Ì S; f || П₂

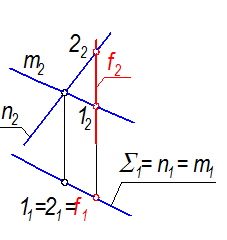
Рис. 2-14

Так как плоскость S - горизонтально проецирующая, то единственная прямая в такой плоскости, параллельная плоскости проекций П₂ - горизонтально проецирующая прямая Þ f ^^ П₁ .