Уравнение бегущей волны

Бегущими волнами называются волны, которые переносят энергию в пространстве. Основной характеристикой бегущей волны является плотность потока энергии переносимой данной волной.

Важными примерами бегущих волн является плоская и сферическая волны. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер.

Уравнением бегущей волны – называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении в ней рассматриваемой волны.

Найдем вид функции ξ в случае бегущей волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось х совпала с направлением рас­пространения волны. Тогда волновые поверхности будут перпендикулярными к оси х и, поскольку все точки волновой поверхности колеблются одинаково, смещение ξ будет зависеть только от х и t:

ξ = ξ{х, t).

Пусть колебания точек, лежащих в плоскости х=0 (рис.17.2.), имеют вид

x(0,t)=А соs(wt+a),

Найдем вид колебания точек в плоскости, соответствующей про­извольному значению X. Для того чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время

τ=x/υ

где υ — скорость распространения волны.

Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на τ от колеба­ний частиц в плоскости х = 0, т. е. будут иметь вид

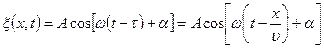(17.2.1)

Выражение (17.2.1) является уравнением плоской волны (и продольной и поперечной), распространяющейся в направлении х, где А=const - амплитуду волны; α - начальная фаза волны (определяется выбором начал отсчета х и t); 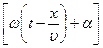-фаза плоской волны.

Если ввести волновое число: ,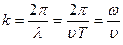

Придем к следующему уравнению плоской вол­ны, распространяющейся вдоль оси х:

x(x,t)=А соs (wt- kx +a). (17.2.2)

или в экспоненциальной форме: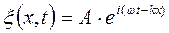

Зафиксируем какое-либо значение фазы, стоящей в уравнении волны (17.2.2)

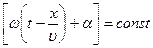или (wt- kx+a)=const

Продифференцировав данное выражение, получим:

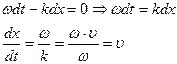
Таким образом, скорость распространения волны в этом уравнении, есть скорость перемещения фазы, в связи с чем, ее называют фазовой скоростью.

Волновое уравнение

Распространение волн в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (17.2.2), описывающую бегущую волну:

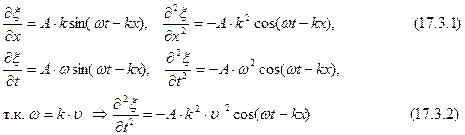
Сравнивая уравнения (17.3.1) и (17.3.2), можно записать

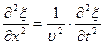
Следовательно, производные по координатам x,y и z

, ,

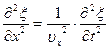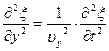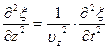
Сложив производные по координатам

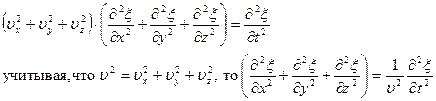
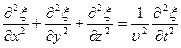- волновое уравнение для плоской волны

Используя, оператор Лапласа

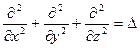
волновое уравнение примет вид

.

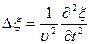Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны).