Сложение однонаправленных колебаний одинаковой частоты

Задача сложения нескольких колебаний может возникнуть, например, в оптике, где световые колебания (колебания вектора напряженности электрического поля) в некоторой точке определяются как результат наложения многих колебаний, приходящих в данную точку от различных участков волнового фронта.

Под сложением колебаний понимают нахождение результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая:

· сложение колебаний одинакового направления;

· сложение взаимно перпендикулярных колебаний.

Рассмотрим первый случай – сложение двух гармонических колебаний одинакового направления и частоты. Для сложения колебаний удобно применять метод векторных диаграмм (рис.16.4).

Суть этого метода в том, что гармоническое колебание представляется при помощи вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью OX угол, равный фазе колебания. Амплитуда и начальная фаза результирующего колебания определяются при помощи векторного сложения. Допустим, что требуется сложить два гармонических колебания:

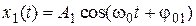и .

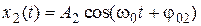Сложим соответствующие им векторы 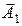и 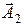для момента времени t. Проекция результирующего вектора 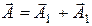на ось Оx равна сумме проекций складываемых векторов 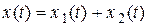. Вектор 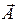представляет собой векторное изображение результирующего колебания (см. рис. 16.4).

Этот вектор в плоскости диаграммы вращается с той же частотой 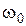, с которой колеблются складываемые осциллирующие функции x₁(t) и x₂(t). Результирующая амплитуда 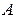и начальная фаза 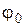находятся геометрическим построением для момента времени t=0:

.

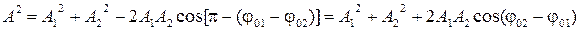
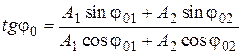Выделим три характерных случая:

· Если разность начальных фаз 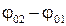обоих колебаний равна 0 или 2pn, где n=1,2,…. то колебания находятся в фазе и амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний:

.

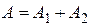· Если разность фаз 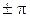, т.е. оба колебания находятся в противофазе, то

,

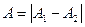при А₁=А₂ наблюдается полное гашение колебаний.

· Если частоты складываемых колебаний не одинаковы, то результирующий вектор пульсирует по величине и вращается с непостоянной скоростью. В этом случае результирующее колебание не будет гармоническим и описывается другими более сложными зависимостями.