Нормально распределенные случайные числа
| № | 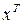
| № | 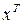
| № | 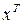
|
| 1. | 0,464 | 13. | -1,010 | 25. | 0,225 |
| 2. | 0,060 | 14. | -0,005 | 26. | 1,678 |
| 3. | 1,486 | 15. | 1,393 | 27. | -0,15 |
| 4. | 1,022 | 16. | 0,137 | 28. | 0,598 |
| 5. | 1,394 | 17. | -2,256 | 29. | -0,899 |
| 6. | 0,906 | 18. | -0,354 | 30. | -1,163 |
| 7. | 1,179 | 19. | -0,472 | 31. | 2,455 |
| 8. | -1,501 | 20. | -0,555 | 32. | -0,531 |
| 9. | -0,69 | 21. | -0,513 | 33. | -0,634 |
| 10. | 1,372 | 22. | -1,055 | 34. | 1,279 |
| 11. | -0,482 | 23. | -0,488 | 35. | 0,046 |
| 12. | -1,376 | 24. | 0,756 | 36. | -0,525 |
Для получения нормально распределенных случайных величин с произвольными значениями 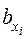 необходимо сделать пересчет по формуле
необходимо сделать пересчет по формуле
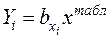 .
.
Для получения коррелированных величин с произвольными значениями 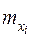 необходимо воспользоваться формулой:
необходимо воспользоваться формулой:
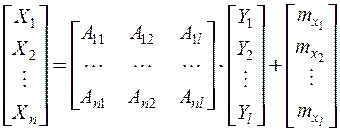 ,
,
где 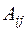 – произвольные постоянные коэффициенты.
– произвольные постоянные коэффициенты.
Требуется найти оценки для числовых характеристик системы: математических ожиданий 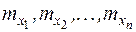 , элементов ковариационной матрицы {
, элементов ковариационной матрицы { 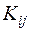 }, элементов нормированной корреляционной матрицы
}, элементов нормированной корреляционной матрицы 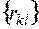 . Оценки для математических ожиданий найдутся как средние арифметические
. Оценки для математических ожиданий найдутся как средние арифметические
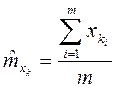 ,
, 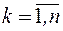 ;
;
несмещенные оценки для дисперсий определятся по формулам
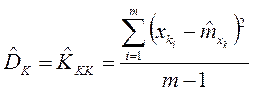 ,
,
для корреляционных моментов – по формулам
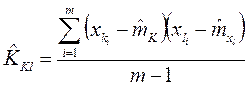 .
.
По этим данным определяются оценки для элементов нормированной корреляционной матрицы
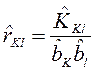 .
.
где 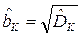 ;
; 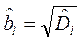 .
.
8.5.2.2. Определить вероятность попадания случайной точки 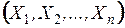 в произвольную область
в произвольную область 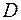
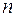 -мерного пространства
-мерного пространства
Вероятность выражается 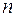 -кратным интегралом по области
-кратным интегралом по области 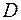
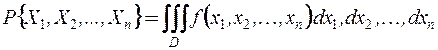 .
.
В случае, если нормально распределенные случайные величины независимы, а область 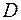 представляет собой
представляет собой 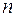 -мерный прямоугольный параллелепипед со сторонами, параллельными координатным осям, то вероятность попадания случайной точки
-мерный прямоугольный параллелепипед со сторонами, параллельными координатным осям, то вероятность попадания случайной точки 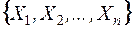 в эту область выражается через функцию Лапласа:
в эту область выражается через функцию Лапласа:
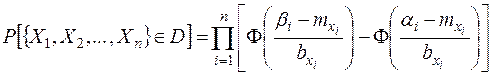 ,
,
где 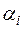 ,
, 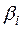 – координаты границ прямоугольного параллелепипеда в направлении оси
– координаты границ прямоугольного параллелепипеда в направлении оси 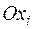
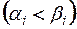 ;
; 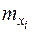 ,
, 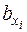 – математическое ожидание и с.к.о. случайной величины
– математическое ожидание и с.к.о. случайной величины 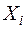 ,
, 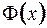 – функция Лапласа.
– функция Лапласа.
8.2.1. Проверка гипотезы о векторе математического ожидания контролируемых параметров большой партии изделий с нормальным законом распределения и известной ковариационной матрицей по выборке малого объема (n1 = 40)
Гипотеза H0: 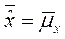 ,
,
где 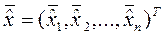 – оценка вектора выборочного среднего;
– оценка вектора выборочного среднего;
где 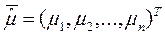 – вектор математического ожидания.
– вектор математического ожидания.
Гипотеза Н1: 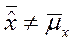 .
.
Вид выборки: любая – большая, малая.
Закон распределения: многомерный нормальный закон распределения. Его плотность записывается в виде
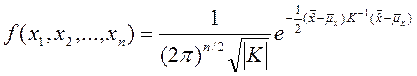 ,
,
где 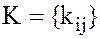 ,
, 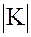 – определитель матрицы K.
– определитель матрицы K.
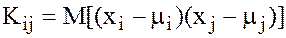 ,
, 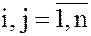 .
.
Статистика: 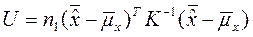 .
.
Закон распределения статистики U – 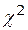 -распределение с числом степеней свободы k = n.
-распределение с числом степеней свободы k = n.
Доверительную область можно получать в n-мерном пространстве в виде 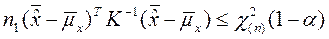 .
.
Эта область представляет собой эллипсоид (в двумерном случае – эллипс).
Пример 8.1. По данным контрольных замеров деталей (табл. 8.2), изготовленных на десяти станках (n1 = 10), проверить гипотезу с уровнем значимости 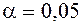 о соответствии средних измеряемых параметров деталей X1, X2, X3 (n = 3) контрольным значениям
о соответствии средних измеряемых параметров деталей X1, X2, X3 (n = 3) контрольным значениям 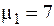 ;
; 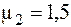 ;
; 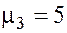 .
.
Ковариационная матрица считается известной

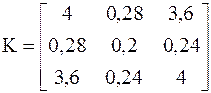 .
.
Исходная информация для сравнения параметров Таблица 8.3
| Номер изделия | № станка | |||||||||
| X1 | ||||||||||
| X2 | 1,2 | 1,2 | 1,4 | 1,2 | 1,2 | 1,5 | 1,5 | 1,3 | 1,7 | 1,6 |
| X3 | 2,1 | 2,8 | 3,2 | 4,5 | 4,8 | 4,9 | 5,5 | 6,5 | 8,5 |
Решение. Исходя из условия задачи, требуется проверить гипотезу H0:

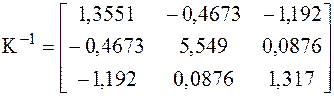 .
.
Получим неравенство 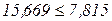 , т.е. гипотеза Н0 отвергается с вероятностью ошибки 0,95.
, т.е. гипотеза Н0 отвергается с вероятностью ошибки 0,95.
Таким образом, средние уровни измеряемых параметров деталей не соответствуют контрольным цифрам.
8.2.2. Проверка гипотезы о векторе математического ожидания контролируемых параметров большой партии изделий с нормальным законом распределения и неизвестной ковариационной матрицей по выборке малого объема (n1 = 40)
В отличие от случая 8.5.2 используется статистика Хоттелинга: 
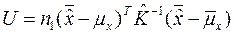 , где
, где 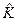 – выборочная ковариационная матрица с элементами
– выборочная ковариационная матрица с элементами 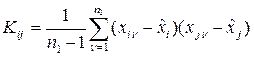 , где
, где 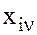 – значение параметра i в v эксперименте.
– значение параметра i в v эксперименте.
Закон распределения статистики 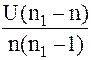 – F-распределение с n (для числителя) и n1 – 1 (для знаменателя) степенями свободы.
– F-распределение с n (для числителя) и n1 – 1 (для знаменателя) степенями свободы.
Доверительную область можно получить в n-мерном пространстве в виде
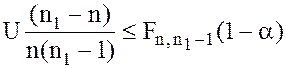 .
.
Это снова эллипсоид.
Пример 8.2. В условиях предыдущего примера решить задачу при неизвестной ковариационной матрице.
Решение. Требуется проверить гипотезу H0: 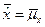 против H1:
против H1: 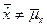 .
.
Прежде всего, находим оценку ковариационной матрицы:
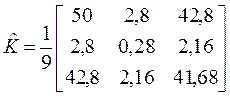 .
.
Значение функции F-распределения 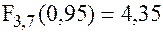 .
.
Получаем соотношение 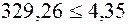 , которое говорит о том, что гипотеза Н0 и в этом случае отвергается с вероятностью 0,95.
, которое говорит о том, что гипотеза Н0 и в этом случае отвергается с вероятностью 0,95.
8.2.3. Проверка гипотезы о средних значениях n контролируемых параметров двух больших партий изделий с нормальным законом распределения и известной ковариационной матрицей по выборке малого объема (n1 = 40; n2 = 40)
Гипотеза H0: 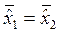 ,
,
Гипотеза H1: 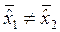 .
.
Вид выборки: любая – большая, малая.
Закон распределения: многомерные нормальные законы распределения 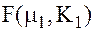 ,
, 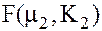 .
.
Статистика: 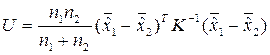 .
.
Закон распределения статистики U - 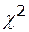 -распределение с числом степеней свободы k = n.
-распределение с числом степеней свободы k = n.
Доверительная область определяется условием
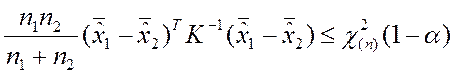 .
.
Эта область представляет собой эллипсоид.
8.2.4. Проверка гипотезы о средних значениях n контролируемых параметров двух больших партий изделий с нормальным законом распределения и неизвестной ковариационной матрицей по выборке малого объема (n1 = 40; n2 = 40)
В отличие от случая 8.5.3 используется статистика:
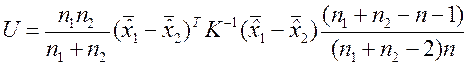 ,
,
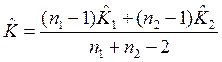 .
.
Здесь 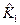 ,
, 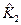 – ковариационные матрицы партий № 1, № 2.
– ковариационные матрицы партий № 1, № 2.
Закон распределения статистики U – F-распределение с n (для числителя) и (n1 + n2 – n – 1) (для знаменателя) степенями свободы.
Доверительную область получим из условия:
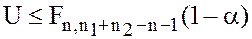 .
.
Как и ранее, это снова эллипсоид.
Подробные таблицы математической статистики можно взять из учебного пособия [1].
8.3. Методические рекомендации к теоретическому разделу 1.
Целесообразно при оценивании параметров распределений формируемых статистик отследить влияние на точность оценок размера выборки. Следует при этом убедиться, что при переходе к интервальному (доверительному) оцениванию точность оценок не повышается. Такой прием (интервальное оценивание) позволяет знать точность и надежность (достоверность) оценки и не более.
Одним из путей повышения точности оценок является увеличение объема выборки n1.
Дата добавления: 2016-12-09; просмотров: 2785;











