Основные сведения из теории

<16 17 181920 21 22 >

Рассмотрим нормальное распределение для системы произвольного числа 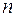случайных величин – вектора 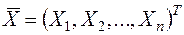в 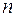-мерном пространстве. Его плотность записывается в виде:

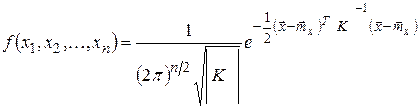, (8.1)

где

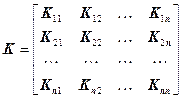, (8.2)

. (8.3)

В силу симметрии ковариационной матрицы ( 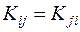) обратная ковариационная матрица также обладает свойством симметрии

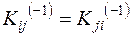. (8.6)

Если нормально распределенные случайные величины независимы (некоррелированы) и при этом 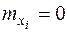, , 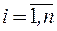то их плотность распределения может быть записана в виде:

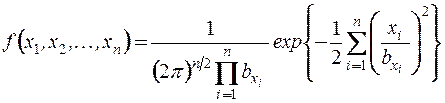, (8.7)

которая называется канонической (простейшей) формой нормального закона системы 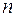случайных величин .

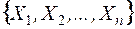Для наглядного представления плотности распределения можно получить уравнение 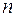-мерного гиперэллипсоида из условия

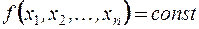, (8.8)

или для случая (8.7)можно записать

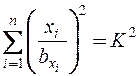(8.9)

При 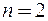получаем уравнение эллипса равной плотности в декартовой прямоугольной системе координат на плоскости (рис.5.1):

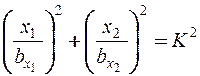(8.10)

Центр этого эллипса находится в начале координат, его полуоси равны: ; .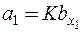

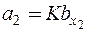Рис.8.1. Уравнение эллипса равной плотности

При 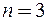получим уравнение эллипсоида равной плотности в декартовой прямоугольной системе координат в пространстве трех измерений (рис.8.2):

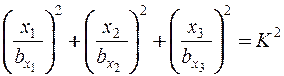(8.11)

Центр этого эллипсоида находится в начале координат, его полуоси равны: ; ; .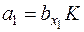

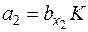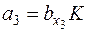Рис. 8.2. Уравнение эллипсоида равной плотности

<16 17 181920 21 22 >

Дата добавления: 2016-12-09; просмотров: 1358;