Критерий согласия законов распределения А.Н. Колмогорова
На практике и в данной лабораторной работе возможны ситуации, когда при обработке данных о распределении ничего неизвестно, поэтому желательно иметь критерии согласия, свободные от конкретного закона распределения. Таким критерием является критерий согласия Колмогорова. В качестве меры близости взято максимальное значение модуля разности между статистической функцией распределения 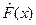 и соответствующей теоретической функцией распределения F(x).
и соответствующей теоретической функцией распределения F(x).
Схема применения критерия Колмогорова может быть представлена последовательностью шагов:
1. Находится 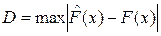 .
.
2. Определяется величина 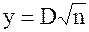 . В лабораторной работе за n будем считать величину выборки, использованной для построения
. В лабораторной работе за n будем считать величину выборки, использованной для построения 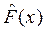 .
.
3. По таблице «Функция распределения Колмогорова» находится вероятность 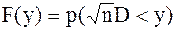 .
.
Если вероятность F(y) мала, например, 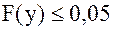 , то гипотезу о соответствии двух законов распределений следует считать правдоподобной, совместимой с опытными данными. Таблица формируется программно в лабораторной работе.
, то гипотезу о соответствии двух законов распределений следует считать правдоподобной, совместимой с опытными данными. Таблица формируется программно в лабораторной работе.
Функция распределения Колмогорова
Таблица 7.2.
| Y | ||||||||||
| 0,3 | 0,0000 | |||||||||
| 0,5 | 0,0360 | |||||||||
| 1,0 | 0,7300 | |||||||||
| 1,5 | 0,9778 | |||||||||
Дата добавления: 2016-12-09; просмотров: 1874;











