Оперативно-статистический контроль качества продукции (одномерный случай).
Открыть программу «Оперативно-статистический контроль», в которой проверяется девять гипотез, описанных в пп. 7.1.1 - 7.1.9.
Опишем работу первого варианта. Пусть математическое ожидание проверяемого параметра в партии изделий равно 10, а дисперсия равна 1. Эти значения вводятся при соответствующем запросе в программе. Необходимо просмотреть значения параметров с номерами от 0 до 499 (т.е. генеральная совокупность составляет 500 объектов). Выбираем любые номера объекта и получаем значение математического ожидания. Например:
| Номер объекта | ||||||||||
| Значение mx | 10,839 | 9,592 | 7,740 | 9,017 | 10,166 | 13,486 | 9,871 | 10,318 | 9,414 | 9,858 |
Записать таблицу в тетрадь. Затем на экране появится следующая таблица:
| Интервал | F’(U) | F(U)среднее | |F’(U) – F(U)| |
| -2,293; -1,737 | 0,025 | 0,030 | |
| -1,737; -1,181 | 0,126 | 0,098 | |
| -1,181; -0,625 | 0,223 | 0,225 | |
| -0,625; -0,069 | 0,295 | 0,364 | |
| -0,069; 0,487 | 0,435 | 0,419 | |
| 0,487; 1,043 | 0,413 | 0,343 | |
| 1,043; 1,599 | 0,190 | 0,200 | |
| 1,599; 2,155 | 0,065 | 0,082 | |
| 2,155; 2,711 | 0,025 | 0,024 |
Где 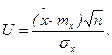
Заполнить таблицу в тетради. Построить гистограммы теоретического и практического распределений.
Открыть приложение MS Excel.
В диапазоне (A1:I9) записать вспомогательную матрицу А(9х9).
В десятой строке записана длина интервала (вычислить самостоятельно).
В массиве (А12:А21) записаныэкспериментальные значения параметра А, взятые из таблицы. В диапазоне (В12:В21), отражающем вероятность (видно, что сумма значений близка к 1), применена формула Ai*0,556. В диапазоне (С12:С21) записана формула умножения матрицы А на столбец В.
В столбцах E, F и G, отражающих теоретические данные, проделаны те же операции, что и для экспериментальных. В столбце Н просчитана абсолютная разность между 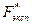 и Ft и найдено ее максимальное значение (ячейка Н21).
и Ft и найдено ее максимальное значение (ячейка Н21).
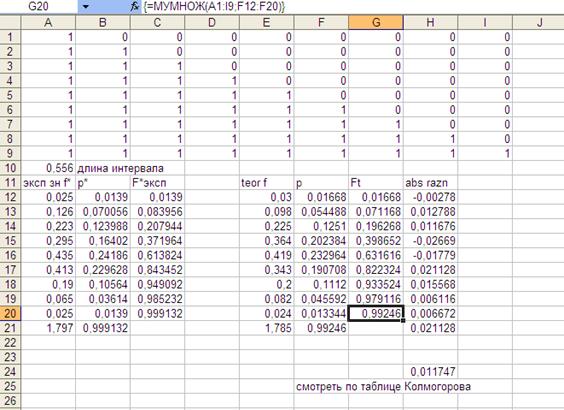 Рис. 7.4. Проверка статистической гипотезы о математическом ожидании контролируемого параметра.
Рис. 7.4. Проверка статистической гипотезы о математическом ожидании контролируемого параметра.
В ячейке Н23 (формула Н21*0,556) находится то экспериментальное значение, на основании которого можно сделать вывод о принятии или не принятии нулевой гипотезы. Критическое значение статистики найдем из таблицы Колмогорова. В нашем случае при ошибке 0,05 оно равно 0,52, т.е. U<Uкр. Это говорит о пригодности партии готовой продукции.
В том, что экспериментальный закон практически полностью совпадает с теоретическим, можно убедиться, построив в одной системе координат их графики (столбцы C и G).
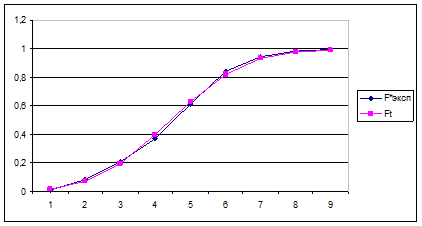
Рис.7.5. Графики интегральных функций распределения теоретических и экспериментальных данных.
Дата добавления: 2016-12-09; просмотров: 1886;











