Определение главных компонент дискретного конечного множества элементов.

Объект контроля может характеризоваться большим количеством параметров. Среди них можно выделить наиболее информативные (главные). Это достигается снижением размерности исходных данных с помощью нейросетевого алгоритма.

Если объект характеризуется n параметрами x_j , где j = 1,2,…,n, то можно перейти к m параметрам y_i , где i=1,2,…,m (n > m) за счет преобразования Y = W*X.

Пример. Имеются данные о росте и длине правой и левой рук (от плеча до кончиков пальцев) у 5 человек. Таким образом, имеются 3 параметра. Сократим число параметров до двух информативных.

Реализуем определение главных компонент с помощью нейронной сети в программе MS Excel.

В массиве (C2:G9) записываем исходные данные.Т.о., исходная матрица Х(3х5). Искомая матрица Y должна иметь размерность (2х5) (массив (С8:G9)). Значит, матрица весовых коэффициентов W (2х3) – массив (B6:D7). Первоначально все коэффициенты в матрице W равны 1.

Массив (В10:С12) – транспонируем W.

Массив (С14:G16) – возвращаемся к переменной Х. Получаем матрицу ХА(3х5). В массиве (С18:G20) вносим формулы квадратов отклонений между соответствующими точками матриц Х и ХА, т.е. в ячейку С18 записываем формулу =(С2-С18)^2 и копируем в другие ячейки.

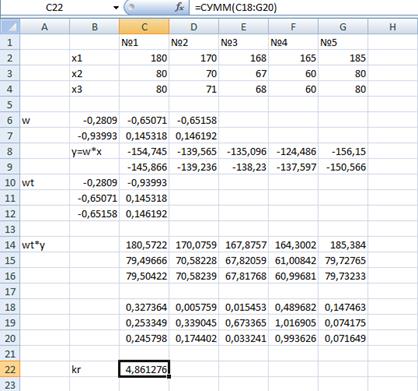
Рис. 10.1. Метод главных компонент.

Ячейка С22 – сумма всех квадратов отклонений. Для нахождения коэффициентов w_ij воспользуемся инструментом Поиск решения. В данном случае применяется алгоритм поиска минимума целевой функции в ячейке С22. При этом весовые коэффициенты w_ij изменяются. Поэтому ячейками изменения будет массив (B6:D7). Нажимаем кнопку Выполнить. Алгоритм минимизации можно применить несколько раз, пока минимальная функция не станет постоянной. Но часто оптимальное значение целевой функции достигается за одну итерацию.

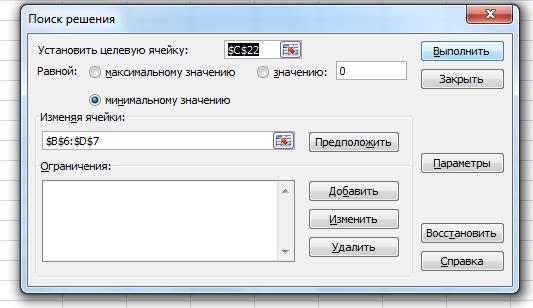
Рис. 10.2. Минимизация целевой функции.