Анализ основных видов одномерного течения
Для практического исследования фильтрационных потоков необходимо знать распределение не абстрактной функции – потенциала, а конкретных физических параметров – давления, скорости, закона движения и так далее. Следовательно, необходим переход от зависимостей (3.3, 3.7–3.10) к соотношениям, определяющим вышеперечисленные параметры при использовании приведенных в разделе 3.2.3. выражений для потенциальной функции. При этом рассмотрим только случай плоскорадиального течения, так как оно имеет наибольший практический интерес.
Течение несжимаемой жидкости через недеформируемый (пористый) пласт.Выражение для потенциала (2.5) запишется в виде
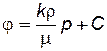 .
.
Выпишем ранее выведенные соотношения в случае плоскорадиального течения для:
· распределения потенциала 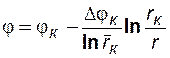 ;
;
· распределения градиента потенциала 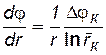 ;
;
· дебита 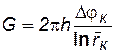 ;
;
· средневзвешенного давления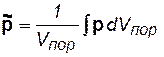 .
.
В вышеприведенных соотношениях: 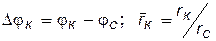 .
.
Для определения закона движения частиц жидкости проинтегрируем уравнение движения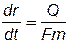 по времени от 0 до t и по расстоянию от r0до r, где r0 – начальное положение частицы флюида.
по времени от 0 до t и по расстоянию от r0до r, где r0 – начальное положение частицы флюида.
Переходя в вышеприведенных соотношениях от потенциала к давлению, получим искомые выражения, позволяющие провести исследование в физических переменных (табл. 3.3).
Таблица 3.3
| Закон фильтрации Дарси | 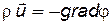
|
| Распределение давления | 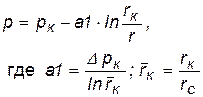
|
| Градиент давления | 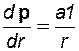
|
| Уравнение притока | 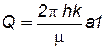
|
| Уравнение движения | 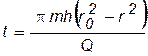
|
| Средневзвешенное давление | 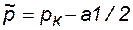 , т.к. , т.к.
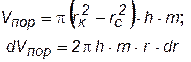
|
Примечание. При выводе соотношения для средневзвешенного давления интеграл не берется в конечном виде. Поэтому подинтегральное выражение приводится к виду 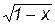 и раскладывается в ряд Тейлора. Беря первые два члена ряда, а именно, 1 –х/2, получаем выражение, которое можно интегрировать по частям. После пренебрежения членами с r2c получаем вышеприведенное соотношение.
и раскладывается в ряд Тейлора. Беря первые два члена ряда, а именно, 1 –х/2, получаем выражение, которое можно интегрировать по частям. После пренебрежения членами с r2c получаем вышеприведенное соотношение.
Дата добавления: 2020-03-17; просмотров: 967;











