ОХЛАЖДЕНИЕ (НАГРЕВ) ОДНОМЕРНЫХ ТЕЛ

Для одномерных тел (неограниченной пластины и бесконечно длинного цилиндра) дифференциальное уравнение теплопроводности (2.53) с учетом (2.57) приводится к виду:

для пластины

∂θ / ∂t =α ∂²θ / ∂x²; (2.65)

для цилиндра

∂θ / ∂t = α( ∂²Т / ∂r² + (1/r)(∂Т / ∂r). (2.66)

При Fo ≥ 0,3 уравнение (2.62), описывающее изменение во времени безразмерной температуры θ_ц/θ_о на средней плоскости пластины (стенки) x = 0, оси цилиндра r = 0 , примет вид:

θ_ц/θ_о = N(Bi)exp(-μ₁²Fo), (2.67)

а на поверхностях этих тел:

θ_ст/θ_о = P(Bi)exp(-μ₁²Fo), (2.68)

где N(Bi) и P(Bi) – функции, зависящие от Bi;

μ₁ - первый корень характеристического трансцендент-

ного уравнения μ=μ(Bi).

Применение уравнений (2.67) и (2.68) на практике связано с необходимостью выполнения трудоемких расчетов. Поэтому для тел простой формы (пластины, цилиндра ), размеры которых представлены на рис. 2.10, с помощью этих уравнений построены графики, использование которых сводит расчеты к весьма простым операциям.

На рис. 2.11 – 2.14 представлены графики функций θ_ц/θ_о = f ( Fo, Bi)

и θ_ст./θ_о = f ( Fo, Bi) для ξ/l = 0 и ξ/l = 1, которые соответственно характеризуют температуру плоскости (оси) симметрии и поверхностей стенки и цилиндра. Прежде, чем воспользоваться графиками для

Рис. 2.10. Форма и размер тела

определения температуры тела, необходимо вычислить значения чисел Био и Фурье. Аналогичные графики имеются и для шаров.

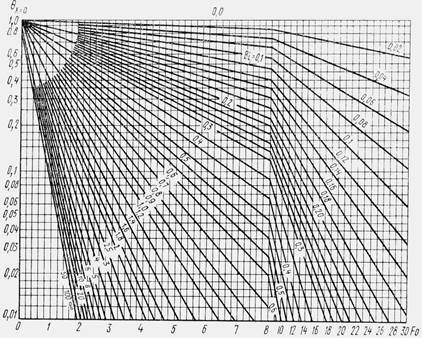
Рис.2.11. Безразмерная температура в середине бесконечной пластины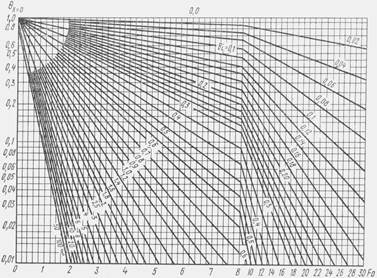

Рис.2.12. Безразмерная температура на поверхности бесконечной

пластины

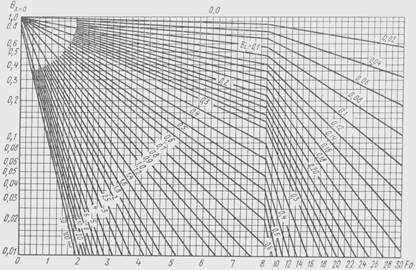
Рис.2.13. Безразмерная температура на оси цилиндра бесконечной

длины

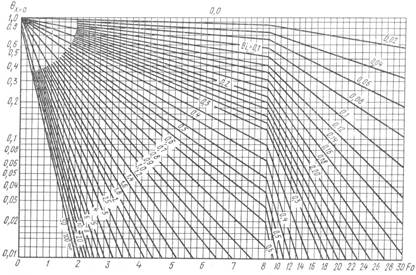
Рис.2.14. Безразмерная температура на поверхности цилиндра

бесконечной длины

Из рис. 2.12 и 2.14 видно, что при Bi ≥ 100 температура стенки перестает зависеть от условий теплообмена на границах тела. Это объясняется тем, что при этом тепловое сопротивление внешнего теплообмена становится неизмеримо малым по сравнению с внутренним сопротивлением, и потому температурное поле определяется условиями распространения теплоты внутри тела.

Для решения некоторых задач об охлаждении или нагревании тел сложной конфигурации разработаны приближенные методы решения, из которых чаще всего применяютметод конечных разностей.

Количество полученной или отданной стенкой теплоты также определяется числами Fo и Bi. Обозначим через Q_o количество потерянной (или полученной) теплоты при t → ∞ (когда температуры тела и среды выравниваются), а через Q_t теплоту, отданную (или полученную) по истечении времени t. Тогда для стенки с плотностью материала ρ и теплоемкостью с можно записать:

Q_o = 2δρс(Т_о – Т_ж) = 2δρсθ_о, (2.69)

Q_t = 2δρс(Т_о – Т_ср) = 2δρс(θ_{о –} θ_ср), (2.70)

где Т_ср – средняя температура стенки по истечении периода времени t.

Поделив почленно второе равенство на первое, получим:

Q_t / Q_o = 1 - θ_ср/θ_о. (2.71)

В каждый момент времени температурное поле стенки определяется числами Fo и Bi. Поэтому и средняя температура стенки Т_ср будет зависеть только от этих чисел. Следовательно,

Q_t / Q_o = f ( Fo, Bi). (2.72)

График этой функции имеется в справочной литературе.