ИЗУЧЕНИЕ СОУДАРЕНИЯ ШАРОВ
Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
Удар (или соударение) – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. При ударе тела испытывают деформацию. Явление удара протекает обычно в сотые, тысячные и миллионные доли секунды. Время соударения тем меньше, чем меньше деформации тел. Так как при этом количество движения тел изменяется на конечную величину, то при соударении развиваются огромные силы.
Процесс удара разделяют на две фазы.
Первая фаза – с момента соприкосновения тел до момента, когда их относительная скорость становится равной нулю.
Вторая фаза – от этого последнего момента до момента, когда соприкосновение тел прекращается.
С момента возникновения деформаций в местах соприкосновения тел начинают действовать силы, направленные противоположно относительным скоростям тел. При этом происходит переход энергии механического движения тел в энергию упругой деформации (первая фаза удара).
Во второй фазе удара, когда относительная скорость стала равной нулю, начинается частичное или полное восстановление формы тел, затем тела расходятся и удар заканчивается. В этой фазе кинетическая энергия системы растет за счет положительной работы упругих сил.
У реальных тел относительная скорость после удара не достигает той величины, которую она имела до удара, так как часть механической энергии необратимо переходит во внутреннюю и другие формы энергии.
Различают два предельных типа удара:
а) удар абсолютно неупругий;
б) удар абсолютно упругий.
Абсолютно неупругий удар (близкий к нему) возникает при столкновении тел из пластических материалов (глина, пластилин, свинец и др.), форма которых не восстанавливается после прекращения действия внешней силы.
Абсолютно неупругим ударом называется удар, после которого возникшие в телах деформации полностью сохраняются. После абсолютно неупругого удара тела движутся с общей скоростью.
Абсолютно упругий удар (близкий к нему) возникает при столкновении тел из упругих материалов (сталь, слоновая кость и др.0, форма которых после прекращения действия внешней силы полностью (или почти полностью) восстанавливается. При упругом ударе восстанавливается форма тел и величина их кинетической энергии. После удара тела движутся с разными скоростями, но сумма кинетических энергий тел до удара равна сумме кинетических энергий после удара. Прямая, совпадающая с нормалью к поверхности тел в точке их соприкосновения, называется линией удара. Удар называется центральным, если линия удара проходит через центры тяжести тел. Если векторы скоростей тел до удара лежали на линии удара, то удар называется прямым.
При соударении тел выполняются два закона сохранения.
1. Закон сохранения импульса.
В замкнутой системе (система, для которой результирующая всех внешних сил равна нулю) векторная сумма импульсов тел 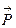 не изменяется, т.е. величина
не изменяется, т.е. величина 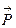 постоянная:
постоянная:
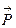 =
= 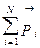 =
= 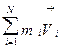 = const, (4.1)
= const, (4.1)
где 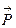 – полный импульс системы,
– полный импульс системы,
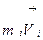 – импульс i –го тела системы.
– импульс i –го тела системы.
2. Закон сохранения энергии
В замкнутой системе тел сумма кинетической, потенциальной и внутренней энергии остается величиной постоянной:
Wк + Wn + Q = const, (4.2)
 где Wк – кинетическая энергия системы,
где Wк – кинетическая энергия системы,
Wn – потенциальная энергия системы,
Q – энергия теплового движения молекул (тепловая энергия).
Простейшим случаем соударения тел является центральный удар двух шаров. Рассмотрим удар шаров массами mi и m2.
Скорости шаров до удара 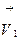 и
и 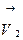 после удара
после удара 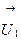 и
и 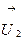 . Для них законы сохранения импульса и энергии запишутся так:
. Для них законы сохранения импульса и энергии запишутся так:
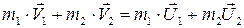 , (4.3)
, (4.3)
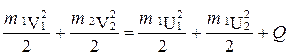 . (4.4)
. (4.4)
Удар шаров характеризуется коэффициентом восстановления К, который определяется отношением относительной скорости шаров после удара 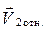 к относительной скорости шаров до удара
к относительной скорости шаров до удара 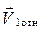 ., взятое по абсолютной величине т.е.
., взятое по абсолютной величине т.е.
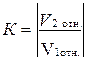 . (4.5)
. (4.5)
Скорости первого шара относительно второго до и после удара равны:
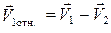 ,
, 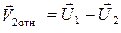 . (4.6)
. (4.6)
Тогда коэффициент восстановления шаров равен:
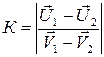 . (4.7)
. (4.7)
При абсолютно упругом ударе выполняется закон сохранения механической энергии, Q = 0, относительные скорости шаров до и после взаимодействия равны и коэффициент восстановления равен 1.
При абсолютно неупругом ударе механическая энергия системы не сохраняется, часть ее переходит во внутреннюю. Тела деформируются. После взаимодействия тела двигаются с одинаковой скоростью, т.е. их относительная скорость равна 0, поэтому коэффициент восстановления тоже равен нулю, К = 0. Закон сохранения импульса запишется в виде
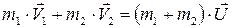 , (4.8)
, (4.8)
где 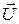 – скорость тел после взаимодействия.
– скорость тел после взаимодействия.
Закон сохранения энергии примет вид:
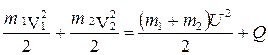 . (4.9)
. (4.9)
Из уравнения (4.9) можно найти Q – механическую энергию, перешедшую во внутреннюю.
На практике предельные случаи взаимодействия осуществляются редко. Чаще взаимодействие носит промежуточный характер, и коэффициент восстановления К имеет значение:
0 £ К £ 1.
Чем ближе значение К к 1, тем меньше доля механической энергии, которая переходит во внутреннюю, тем с меньшей погрешностью удар можно отнести к разряду упругих. К упругим телам относятся, например, сталь, дерево, пластмасса. Коэффициент восстановления стальных шаров 0,8 – 0,9. К пластическим телам относятся глина, пластилин, воск и т.д., коэффициент восстановления для них близок к нулю.
Рассмотрим частный случай, когда массы шаров равны, т.е.
m1 = m2 = m.
Если до взаимодействия первый шар имел скорость V1, а второй был неподвижен (V2 = 0), то по закону сохранения импульса будем иметь:
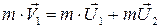 (4.10)
(4.10)
или
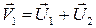 . (4.11)
. (4.11)
Из (4.7) для коэффициента восстановления К имеем:
К = 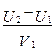 . (4.12)
. (4.12)
Решая совместно уравнения (4.11) и (4.12), получим:
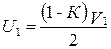 , (4.13)
, (4.13)
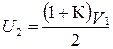 . (4.14)
. (4.14)
В случае абсолютно упругого удара К = 1, тогда U1 = 0, а U2 = V1. Шары при ударе обменивается импульсами. При абсолютно неупругом ударе К = 0 и
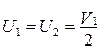 . (4.15)
. (4.15)
Методика работы и описание установки.Установка состоит из двух шаров А и B на бифилярных подвесах, укрепленных на кронштейне F (рисунок 4.1)
Длину нитей можно изменять с помощью винтов и тем самым осуществлять центровку шаров. Установка снабжена шкалой S для измерения углов отклонения шаров и магнитами М1 и М2, при помощи которых шары удерживаются в отклоненном положении.
Если шар отклонить от положения равновесия, он приобретет скорость V. Ее можно найти, использовав закон сохранения энергии.
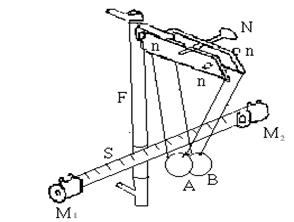
Рисунок 4.1
В отклоненном положении (рисунок 4.2) шар обладает запасом потенциальной энергии Wп = mgh.
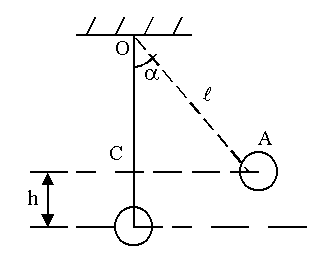
Рисунок 4.2
Высоту h можно определить из треугольника ОАС:
ОС = l – h = l cosa,
откуда
h = l(1 – cos a) = 2lsin2 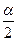 . (4.16)
. (4.16)
При прохождении положения равновесия шар обладает кинетической энергией
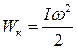 , (4.17)
, (4.17)
где I – момент инерции шара,
w – его угловая скорость в момент прохождения положения равновесия.
Если радиус шара R значительно меньше длины нити l, то шар можно считать материальной точкой, момент инерции которой равен I = ml2, а угловая скорость 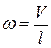 .
.
Подставив I и w в формулу кинетической энергии, получим:
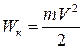 . (4.19)
. (4.19)
По закону сохранения энергии:
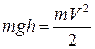 , (4.20)
, (4.20)
откуда
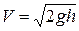 . (4.21)
. (4.21)
Подставив в (4.21) h (4.16), получим:
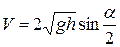 . (4.22)
. (4.22)
Для определения отношения масс шаров воспользуемся законом сохранения импульса, если один из шаров неподвижен (например, второй шар):
m1V1 = m1U1_+ m2U2, (4.23)
где m1V1 – импульс первого шара до удара,
m1U1 – импульс первого шара после удара,
m2U2 – импульс второго шара после удара.
Из формулы (4.23) имеем:
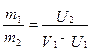 (4.24)
(4.24)
или, учитывая соотношение (4.22), получим:
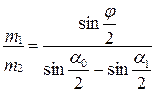 , (4.25)
, (4.25)
где aо – угол отклонения первого шара до удара,
a1 – угол отклонения первого шара после удара,
j – угол отклонения второго шара после удара.
При определении коэффициента восстановления шаров их отклоняют перед ударом на одинаковый угол aо. Если шары имеют равные массы, то скорости до и после удара будут равными, т.е.
V1 = V2 =V и U1 = U2 = U.
Поэтому для коэффициента восстановления шаров будет иметь:
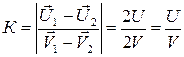 . (4.26)
. (4.26)
Откуда: U = КV.
Следовательно, можно записать систему уравнений:
После первого удара: U1 = КV.
После второго удара: U2 = КU1.
и.т.д.
После n- го удара: Un = КUn-1.
Перемножив равенства и произведя сокращения, получим:
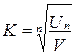 , (4.27)
, (4.27)
где V – скорость любого из шаров до удара,
Un – скорость этого же шара после n –го удара.
Подставив в (4.27) V и Un с учетом (4.22), получим:
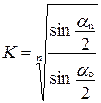 , (4.28)
, (4.28)
где aо – угол отклонения шара до удара,
an – угол отклонения шара после n –го удара.
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ МАЯТНИКА
Гармоническим колебанием физической величины a называется процесс изменения ее за время t по закону гармонической функции, например:
a = Asin(w t + jo), (5.1)
где А – амплитуда колебаний – максимальное значение колеблющейся величины,
w – циклическая частота колебания, величина j = w t + jo носит название фазы колебания,
jo – начальная фаза колебаний.
(jo = const). График такого колебания представлен на рисунке 5.1.
Периодом колебания называется промежуток времени, за который совершается одно полное колебание. При этом фаза колебания изменится на 2p, т.е. w (t + T) + jo = w t + jo + 2p,
откуда
w = 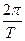 . (5.2)
. (5.2)
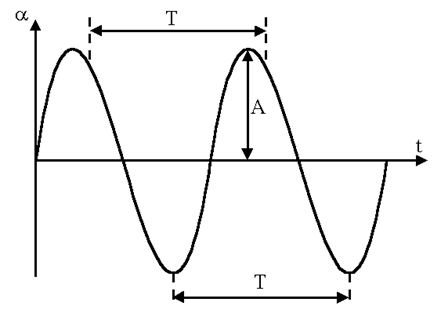
Рисунок 5.1
Величина w – круговая (циклическая) частота колебания, характеризует изменение фазы колебания за единицу времени.
Если начальная фаза jo равна 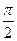 , то уравнение гармонического колебания записывается в виде:
, то уравнение гармонического колебания записывается в виде:
a = Acosw t. (5.3)
Примерами гармонических колебаний являются колебания физического и математического маятников.
Физическим маятником называется тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относительно этой оси (рисунок 5.2).
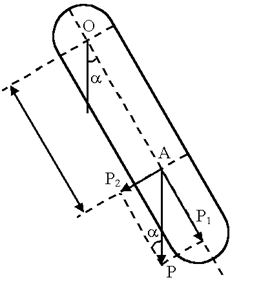
Рисунок 5.2
Математический маятник – это идеализированная система, состоящая из материальной точки m, подвешенной на нерастяжимой невесомой нити и колеблющейся под действием силы тяжести. Хорошим приближением математического маятника является тяжелый шарик, подвешенный на тонкой длинной нити (диаметр шарика во много раз меньше длины нити, масса которой во много раз меньше массы шарика), второй конец которой закреплен неподвижно.
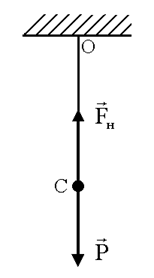 Рисунок 5.3 Рисунок 5.3
| 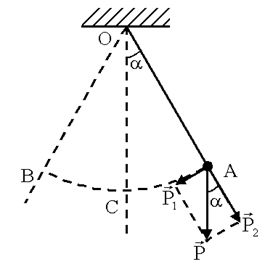 Рисунок 5.4 Рисунок 5.4
|
Если груз маятника неподвижен и находится в положении равновесия (рисунок 5.3), на него действуют сила тяжести 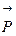 =
= 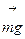 и сила натяжения
и сила натяжения 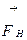 . Эти силы уравновешивают друг друга (направлены в противоположные стороны
. Эти силы уравновешивают друг друга (направлены в противоположные стороны 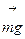 = –
= – 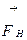 ).
).
Докажем, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания. При отклонении маятника на угол a от положения равновесия силу тяжести 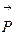 =
= 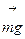 можно разложить на две составляющие (рисунок 5.4)
можно разложить на две составляющие (рисунок 5.4)
ê 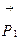 ê =
ê = 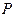 sina и ê
sina и ê 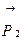 ê =
ê = 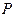 cosa. (5.4)
cosa. (5.4)
Сила 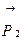 уравновешивает силу натяжения
уравновешивает силу натяжения 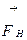 Составляющая P1 направлена вдоль касательной к траектории движения маятника (движение по дуге окружности АС к положению равновесия с ускорением).
Составляющая P1 направлена вдоль касательной к траектории движения маятника (движение по дуге окружности АС к положению равновесия с ускорением).
В положении равновесия (×) С ê 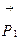 ê = 0, шарик по инерции проходит это положение, а затем его движение становится замедленным до положения (×) B. После максимального отклонения от положения равновесия на угол a шарик будет двигаться обратно и такие движения будут повторяться многократно – шарик будет колебаться.
ê = 0, шарик по инерции проходит это положение, а затем его движение становится замедленным до положения (×) B. После максимального отклонения от положения равновесия на угол a шарик будет двигаться обратно и такие движения будут повторяться многократно – шарик будет колебаться.
На основании закона динамики вращательного движения – момент силы lP1 равен произведению момента инерции шарика I на угловое ускорение e, имеем:
P1 l = Ie , (5.5)
где e = a11 = d2a/dt2 – угловое ускорение (вторая производная угла поворота a по времени t),
I =ml2 – момент инерции шарика, относительно оси, проходящей через точку 0 (момент инерции материальной точки),
l – длина маятника,
P1 = – Psina = – mgsina – возвращающая сила (знак “–” обусловлен тем, что P1 и a всегда противоположны).
sina » a при a £ 40 – 60. Поэтому
P1 = – mga (5.6)
и уравнение (5.5) принимает вид:
– mgla = ml2a11,
ga + la11 = 0 (5.7)
или
a11 + 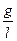 a = 0. (5.8)
a = 0. (5.8)
Обозначив
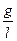 = w02, w0 =
= w02, w0 = 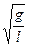 , (5.9)
, (5.9)
получим уравнение:
a11 + w0 2 = 0, (5.10)
где wо – циклическая частота колебаний маятника.
Уравнение (5.10) – уравнение гармонического осциллятора. Решение этого уравнения имеет вид уравнения гармонического колебания
a = aо cos (wо t + jо). (5.11)
Из соотношения (5.11) следует, что при малых углах отклонения математический маятник совершает гармонические колебания с циклической частотой wо и периодом колебания Т.
Т = 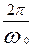 = 2p
= 2p 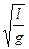 . (5.12)
. (5.12)
Формулу (5.12) периода колебаний математического маятника можно использовать для определения ускорения свободного падения. Из формулы (5.12) следует, что период колебаний математического маятника не зависит от его массы.
Описание установки и теория метода.Математический маятник представляет собой массивный шарик небольшого размера, подвешенный на длинной двойной нити, чтобы колебания происходили строго в одной плоскости (рисунок 5.5).
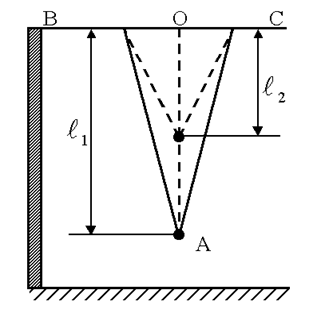
Рисунок 5.5
На перекладине BC подвешен на двойной нити шарик А. Длину математического маятника можно изменять, натягивая нить на барабан. Периоды колебаний математического маятника Т1 и Т2 определяются при разных длинах l1 и l2 по формуле (5.12)
Т1 = 2p 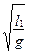 , Т2 = 2p
, Т2 = 2p 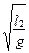 (5.13)
(5.13)
Возводим в квадрат Т1 и Т2
Т1 2 = 4p 2 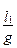 , Т2 2 = 4p 2
, Т2 2 = 4p 2 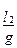
и получим для ускорения свободного падения g следующее соотношение:
g = 4p 2 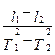 . (5.14)
. (5.14)
Так как в формулу (5.14) входит разность длин маятников, то можно измерить расстояние точки 0 до точки подвеса шарика (×)А (рисунок 5.5).
Дата добавления: 2021-02-19; просмотров: 641;











