ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Вращательное движение характеризуется угловым перемещением φ, угловой скоростью 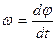 и угловым ускорением
и угловым ускорением 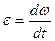 . При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
. При вращательном движении все точки тела имеют одинаковую угловую скорость и угловое ускорение.
Связь линейного и углового перемещений выражается соотношением:
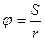 (радиан) (3.1)
(радиан) (3.1)
Тогда 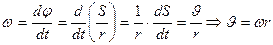 (3.2)
(3.2)
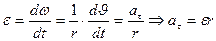 (3.3)
(3.3)
При вращении твердого тела относительно неподвижной оси отдельные его элементарные части с массами 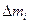 (материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости
(материальные точки) описывают окружности разных радиусов ri и имеют различные линейные скорости 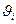 . Но угловая скорость вращения
. Но угловая скорость вращения 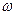 всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
всех этих точек, если тело при вращении не деформируется, одинакова, т.е.
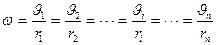 (3.4)
(3.4)
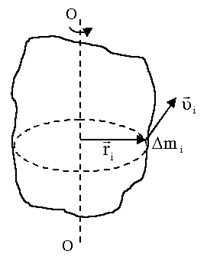
Рисунок 3.1
Кинетическая энергия вращающегося тела Wк определяется как сумма кинетических энергий его составных элементарных масс:
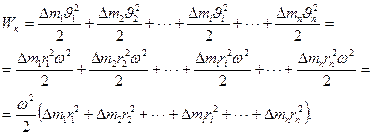 (3.5)
(3.5)
Величину, равную произведению элементарной массы 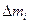 на квадрат расстояния от нее до оси вращения
на квадрат расстояния от нее до оси вращения 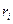 , называют моментом инерции материальной точки
, называют моментом инерции материальной точки
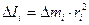 (3.6)
(3.6)
Момент инерции всего твердого тела относительно данной оси вращения равен сумме моментов инерции элементарных масс, составляющих данное тело:
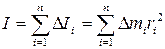 (3.7)
(3.7)
Измеряется момент инерции в кг·м2. Более точно момент инерции можно определить при 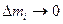 :
:
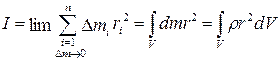 , (3.8)
, (3.8)
где интегрирование производится по всему объему тела.
Из формул (3.5) и (3.7) следует выражение кинетической энергии вращающегося твердого тела:
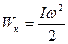 (3.9)
(3.9)
Момент инерции является основной физической величиной, характеризующей инертность твердого тела при вращательном движении.
Момент инерции тела зависит от распределения массы рассматриваемого тела относительно заданной оси вращения (от формы и размеров тела и от расположения оси, относительно которой определяется момент инерции). Для однородных тел правильной геометрической (симметричной) формы момент инерции относительно осей симметрии легко вычисляется.
Рассмотрим момент инерции некоторых тел правильной формы относительно оси симметрии ОО/:
1) Момент инерции материальной точки, т.е. тела, размеры которого много меньше расстояния до оси вращения. Масса тела m ,расстояние до оси вращения ОО/ d (рисунок 3.2):
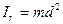 (3.10)
(3.10)
2) Момент инерции тонкостенных колец, цилиндра и обруча относительно оси ОО/ (ri= R) (рисунок 3.3):
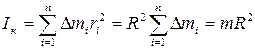 , (3.11)
, (3.11)
где 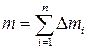 – масса тела;
– масса тела;
R – его радиус.
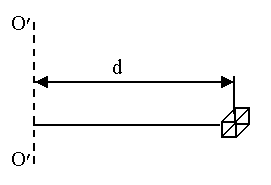
Рисунок 3.2
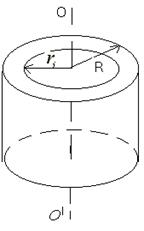
Рисунок 3.3
3) Момент инерции однородного сплошного цилиндра, диска относительно оси ОО/:
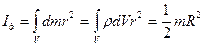 , (3.12)
, (3.12)
где m – масса диска;
R – его радиус.
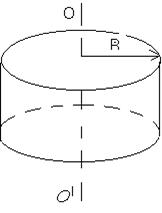
Рисунок 3.4
4) Момент инерции толстостенного кольца относительно оси кольца (рисунок 3.3):
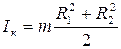 , (3.13)
, (3.13)
где m – масса кольца;
R1 – внутренний радиус;
R2 – внешний радиус.
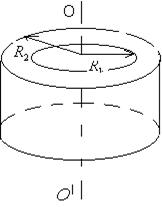
Рисунок 3.5
5) Момент инерции однородного шара относительно оси, проходящей через центр шара:
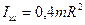 , (3.14)
, (3.14)
где m – масса шара;
R – радиус шара.
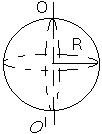
Рисунок 3.6
6) Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно длине l:
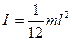 , (3.15)
, (3.15)
где m – масса стержня;
l – длина стержня.
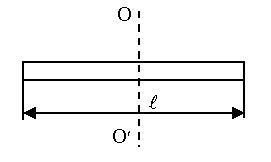
Рисунок 3.7
Из приведенных выше выражений вытекает, что значения моментов инерции тел относительно оси симметрии, проходящей через центр масс, можно представить в виде:
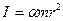 , (3.16)
, (3.16)
где α – коэффициент пропорциональности, зависящий от формы тела.
Если известен момент инерции I0 данного тела относительно оси, проходящей через центр масс этого тела ОО/, то момент инерции I этого тела относительно любой другой оси ХХ/ , параллельной первой и отстоящей от нее на расстоянии а , вычисляется по теореме Штейнера (теорема о влиянии на момент инерции переноса оси вращения)
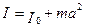 , (3.17)
, (3.17)
где m – масса тела.
Эта теорема может быть выведена непосредственно из определения момента инерции тела относительно произвольной оси (рисунок 3.8).
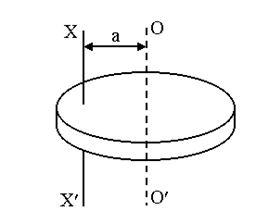
Рисунок 3.8
Теория метода и описание установки.Момент инерции тел сложной формы определяется опытным путем. В данной работе для определения момента инерции тел используется метод крутильных колебаний маятника на трифилярном подвесе, период которого зависит от момента инерции колеблющегося тела.
Маятник на трифилярном подвесе состоит из платформы массой mn и радиусом R (рисунок 3.9), подвешенной на трех металлических нитях, прикрепленных к диску радиусом r<R и расположенных симметрично относительно оси системы ОО/ (ось ОО/ перпендикулярна диску и платформе).
При повороте диска на небольшой угол φ0 вокруг оси центр массы системы несколько приподнимается вдоль оси вращения и нижняя платформа начинает совершать крутильные колебания, период которых зависит от момента инерции системы. Резкий поворот верхнего диска на малый угол φ0<50 почти полностью исключает некрутильные колебания платформы (при колебании платформы верхний диск должен быть неподвижным).
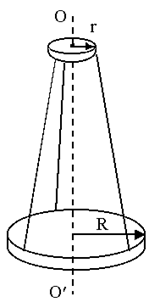
Рисунок 3.9
За четверть периода колебаний платформа поднимется на высоту 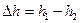 , и ее потенциальная энергия изменится на величину (рисунок 3.10)
, и ее потенциальная энергия изменится на величину (рисунок 3.10)
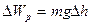 (3.18)
(3.18)
 В следующие четверть периода потенциальная энергия платформы переходит в кинетическую энергию, которая при начальной угловой скорости , равной нулю, запишется так:
В следующие четверть периода потенциальная энергия платформы переходит в кинетическую энергию, которая при начальной угловой скорости , равной нулю, запишется так:
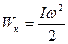 , (3.19)
, (3.19)
где ω – угловая скорость гармонического колебательного движения.
Затем кинетическая энергия переходит в потенциальную и т.д. По закону сохранения и превращения энергии (без учета сил трения) имеем:
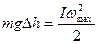 , (3.20)
, (3.20)
где ωmax – максимальная угловая скорость в момент прохождения положения равновесия.
Из этого выражения можно найти момент инерции системы
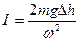 (3.21)
(3.21)
Платформа совершает гармонические крутильные колебания, поэтому угловое смещение φ платформы имеет следующую зависимость от времени:
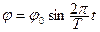 , (3.22)
, (3.22)
где φ0 – угловая амплитуда крутильных колебаний;
T – период полного колебания.
Угловую скорость платформы можно найти, взяв производную по времени от φ :
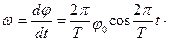 (3.23)
(3.23)
Она максимальна при 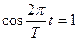 и равна
и равна

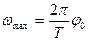 (3.24)
(3.24)
Вычислим величину 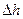 при повороте платформы на угол
при повороте платформы на угол 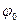 .
.
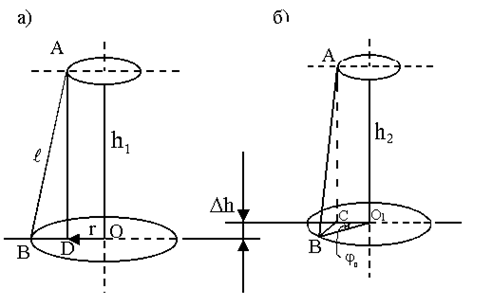
а – положение равновесия маятника;
б – положение максимального смещения маятника.
Рисунок 3.10
Из рисунка 3.10 видно, что
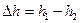 , или
, или
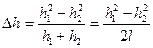 , (3.25)
, (3.25)
так как 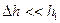 , то
, то 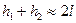
(l – длина нити).
h1 и h2 находим из треугольников ABD и ABC:
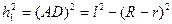 из Δ ABD
из Δ ABD
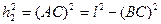 из Δ ABС.
из Δ ABС.
(BC) определяем из треугольника BCO как сторону, лежащую против угла 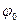 :
:
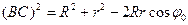 .
.
Тогда 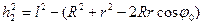 .
.
Подставляем значения 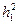 и
и 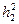 в формулу (3.25), получаем:
в формулу (3.25), получаем:
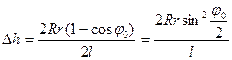 .
.
Так как угол 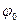 мал, то
мал, то 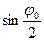 можно заменить аргументом
можно заменить аргументом 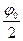 – в радианах:
– в радианах:
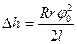 . (3.26)
. (3.26)
Подставляя 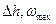 в формулу (3.20), окончательно получаем выражение для расчета момента инерции ненагруженной платформы:
в формулу (3.20), окончательно получаем выражение для расчета момента инерции ненагруженной платформы:
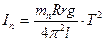 = mnК Т2, (3.27)
= mnК Т2, (3.27)
где mn – масса платформы;
К = 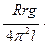 ,
,
R – радиус платформы;
r – радиус диска;
l – длина нити.
(R, r, l, mn – величины постоянные, их значения указаны на установке).
Момент инерции платформы, нагруженной исследуемым телом, вычисляется аналогично:
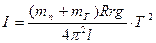 =
= 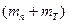 T12 ×К, (3.28)
T12 ×К, (3.28)
где 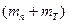 - масса платформы с телом;
- масса платформы с телом;
mT - масса исследуемого тела.
Как видно из выражений (3.27) и (3.28), для определения момента инерции платформы In без тела и момента инерции платформы с исследуемым телом I, необходимо измерить период колебаний крутильного маятника.
Момент инерции исследуемого тела равен разности моментов инерции платформы с исследуемым телом I и без тела In :
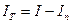 . (3.29)
. (3.29)
В данной лабораторной работе предлагается определить при помощи маятника на трифилярном подвесе момент инерции некоторых тел относительно оси вращения, проходящей через их центр масс, и относительно произвольной оси и проверить теорему Штейнера.
Дата добавления: 2021-02-19; просмотров: 803;











