ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗОВ ПО МЕТОДУ КЛЕМАНА И ДЕЗОРМА

Теплоемкостью вещества называют физическую величину, равную количеству тепла, необходимого для нагревания вещества на один градус 1 °С (или на 1 К).

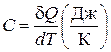, (6.1)

где dQ – бесконечно малое количество тепла, полученное веществом,

dT – бесконечно малое изменение (приращение) его температуры.

Теплоемкость зависит от массы нагреваемого тела. Количество тепла, которое надо сообщить единице массы этого вещества, чтобы повысить его температуру на 1 К (или 1 °С) называют удельной теплоемкостью с:

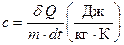. (6.2)

Молярной теплоемкостью С вещества называют физическую величину, численно равную количеству тепла, необходимого для нагревания одного моля вещества на один градус:

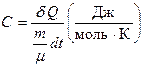, (6.3)

где 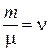– количество вещества – число молей в данной массе.

Из соотношений (6.2) и (6.3) можно определить количество теплоты, получаемое телом:

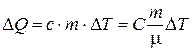(6.4)

и связь удельной и молярной теплоемкостей с и С:

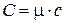, (6.5)

где m – масса одного моля газа.

У твердых и жидких тел величина теплоемкости не зависит от условий их нагревания.

Теплоемкость газов сильно зависит от условий нагревания. Это связано с тем, что подводимое к газу тепло расходуется не только на повышение внутренней энергии газа, которое обуславливает повышение его температуры, но и на совершение работы против внешних сил.

При нагревании газа при постоянном объеме рассматривается теплоемкость при постоянном объеме С_V, при постоянном давлении С_P. Чтобы установить различие между теплоемкостями С_p и С_V, связь между ними, воспользуемся первым началом (законом) термодинамики – всеобщий закон сохранения и превращения энергии, который формулируется так:
количество теплоты dQ, сообщаемое системе, расходуется на увеличение внутренней энергии dU и на совершение системой работы dА над внешними телами (против внешних сил):

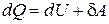, (6.6)

где U – внутренняя энергия системы, т.е. сумма всех видов кинетической и потенциальной энергии всех составных частей системы: молекул, атомов, электронов и т.д.

Для идеального газа внутренняя энергия представляет только кинетическую энергию хаотического, теплового движения молекул и равна:

,

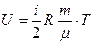где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),
i = 3 для одноатомного газа – поступательные степени свободы,
i = 5 для двухатомного газа – три поступательные и две вращательные степени свободы,
i = 6 для трех и многоатомных газов – три поступательные и три вращательные степени свободы.

Работа газа против сил внешнего давления равна:

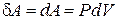, (6.7)

где P – внешнее давление,

dV – приращение объема газа.

Работа dА и теплота dQ – две формы передачи энергии от одного тела к другому.

Рассмотрим применение первого начала термодинамики к изопроцессам для данной массы газа. Изопроцессами называются термодинамические процессы, происходящие при постоянном значении одного из параметров состояния (P, V, T).

1. Изохорический процесс

Изохорический процесс протекает при постоянном объеме V = const, т.е. dV = 0, следовательно, dA = pdV = 0.

Первое начало термодинамики для этого процесса имеет вид:

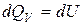, (6.8)

Тепло, подводимое к системе, идет на увеличение ее внутренней энергии (нагревание газа) и из соотношения (6.2) равно:

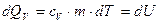, (6.9)

где с_V – удельная теплоемкость при постоянном объеме – количество тепла, которое идет на нагревание 1 кг газа на 1 К при постоянном объеме.

Молярная теплоемкость при постоянном объеме C_V – теплоемкость одного моля:

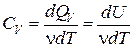, (6.10)

отсюда изменение внутренней энергии для любой массы m равно:

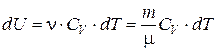. (6.11)

Приращение внутренней энергии идеального газа равно:

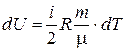, (6.12)

где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),
i = 3 для одно атомного газа – поступательные степени свободы,
i = 5 для двух атомного газа – три поступательные и две вращательные степени свободы,
i = 6 для трех и много атомных газов – три поступательные и три вращательные степени свободы.

Поэтому

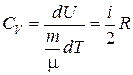. (6.13)

2. Изобарический процесс

Изобарический процесс – процесс, протекающий при постоянном давлении Р = const, dP = 0.

Первое начало термодинамики для этого процесса запишется так:

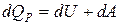. (6.14)

Тепло, подводимое к системе, идет на увеличение внутренней энергии dU и на совершение газом работы над внешними телами dA = PdV.

Из определения молярной теплоемкости (6.3) имеем:

,

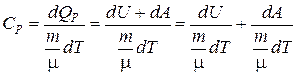где .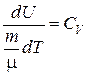

Следовательно, получим

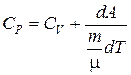. (6.15)

Найдем значение 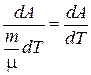для одного моля.

Запишем уравнение Клапейрона-Менделеева для одного моля газа

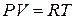. (6.16)

Изменение температуры газа при P = const, прямо пропорционально изменению объема dV, т.е.

,

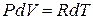где 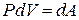- работа газа.

Следовательно,

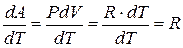, (6.17)

где R – универсальная газовая постоянная.

Учитывая, соотношения (6.15) и (6.17), имеем:

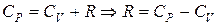(6.18)

– уравнение Майера устанавливает связь между молярными теплоемкостями С_Р и С_V.

Из соотношения (6.17) можно выяснить физический смысл универсальной газовой постоянной – она численно равна работе, совершаемой одним молем газа в результате нагревания на 1 К при постоянном давлении.

Учитывая (6.13) и (6.18), получим:

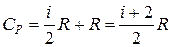. (6.19)

При нагревании 1 моля газа на 1 К при изобарическом процессе часть теплоты C_V идет на увеличение внутренней энергии, и часть, равная R, – на работу против внешних сил.

3. Изотермический процесс

Изотермический процесс – процесс, протекающий при постоянной температуре T = const, dT = 0, P×V = const.

Изменение внутренней энергии .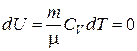

Первое начало термодинамики для этого процесса:

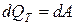. (6.20)

Тепло в этом случае идет только на совершение работы против внешних сил (расширение газа).

В термодинамике, кроме изопроцессов, рассматривается адиабатический процесс.

4. Адиабатический процесс

Адиабатический процесс – процесс, протекающий в условиях полной теплоизоляции, т.е. количество теплоты, получаемое газом равно нулю:

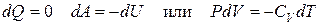, (6.21)

Из первого начала термодинамики следует, что при адиабатическом процессе работа газа над внешними телами совершается за счет уменьшения внутренней энергии. Если объем газа увеличивается, то его температура уменьшается, так как уменьшается его внутренняя энергия.

Для адиабатического процесса имеет место уравнение Пуассона:

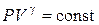, (6.22)

где 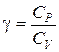– показатель адиабаты. (6.23)

Уравнение 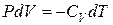для одного моля – первое начало термодинамики в дифференциальной форме. Получим уравнение адиабатического процесса (уравнение Пуассона) в интегральной форме.

Запишем уравнение Клапейрона-Менделеева для одного моля газа:

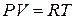(6.24)

и, дифференцируя это уравнение, имеем:

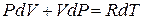. (6.25)

Преобразуем уравнение (6.21) и (6.25), для этого умножим уравнение (6.21) на R, а уравнение (6.25) на C_V:

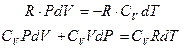
Сложим эти уравнения почленно:

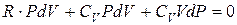
или .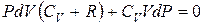

Учитывая, что 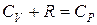(уравнение Майера), получим:

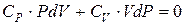. (6.26)

Разделим это уравнение на С_V:

,

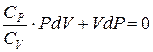где 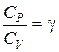- показатель адиабаты.

И тогда можно записать:

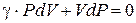. (6.27)

Полученное соотношение является так же, как и (6.21), уравнением адиабаты в дифференциальной форме. Делим обе части этого уравнения на P×V:

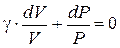, (6.28)

где ,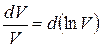

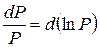, т.е. дифференциалы натуральных логарифмов V и P, поэтому

.

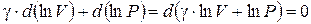Величина, стоящая в скобках, является постоянной, так как ее дифференциал равен нулю. Обозначим ее (ln const). Тогда можем записать:

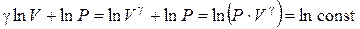
или

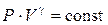. (6.29)

Это соотношение – уравнение адиабаты (Пуассона) (6.22).

Используя соотношения (6.13) и (6.19), можно записать значение показателя адиабаты через степени свободы:

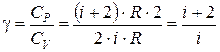. (6.30)

Теория метода и описание установки.Приборы и материалы: баллон с кранами, манометр, насос.

Для определения отношения теплоемкостей в данной работе используется метод, предложенный Клеманом и Дезормом.

Установка для выполнения работы этим методом состоит из стеклянного баллона А (рисунок 6.1) емкостью 15 ¸ 20 литров, соединенного с манометром В и с насосом (на рисунке не показан). Через кран С баллон А соединяется с атмосферой. С помощью крана Д баллон сообщается с насосом. При открытом кране С баллон заполнен воздухом массой m₀ при атмосферном давлении P₀ и комнатной температуре T₀ (состояние 1). На диаграмме P–V (рисунок 6.2) представлена последовательность процессов при выполнении работы. Кран С закрывают и насосом накачивают дополнительную порцию воздуха m.

Давление в баллоне повышается до Р, так как масса газа увеличивается 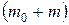, состояние 2 (PTV₁) (рисунок 6.2).

Температура воздуха увеличивается до T, потому что внешние силы совершают работу по сжатию газа массы m₀ при накачивании воздуха 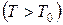. Вследствие теплообмена воздуха с окружающей средой через некоторое время (2 ¸3 мин.) температура воздуха, находящегося в баллоне, сравняется с температурой внешней среды T₀. При этом по манометру можно отметить уменьшение давление воздуха. Когда температура воздуха в баллоне будет равна комнатной (показания манометра перестанут меняться), давление в баллоне станет равным

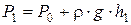, (6.31)

где r×g×h₁ – избыточное давление воздуха в баллоне,
r – плотность жидкости в манометре,
h₁ – разность уровней жидкости в манометре.

Это состояние 3 с параметрами (P₁V₁T₀), где V₁ – объем массы газа m₀.

Затем кран С открывается на короткое время, при этом часть воздуха выходит из баллона, и давление сравнивается с атмосферным P₀. Оставшаяся часть адиабатически расширяется, совершая работу против атмосферного давления; внутренняя энергия газа уменьшается, и температура понижается до T₁ < T₀, состояние 4 (P₀ V₂T₁). Затем кран С быстро закрывают, и воздух в баллоне начинает медленно нагреваться до температуры окружающей среды T₀ – состояние 5 (P₂ V₂T₀), давление при этом увеличивается до P₂.

Понятие адиабатического процесса является идеализацией, так как невозможно полностью исключить обмен теплом между газом и окружающей средой. Но процесс теплообмена идет довольно медленно, поэтому быстрое расширение газа можно рассматривать приближенно адиабатическим.

Давление в баллоне станет равным P₂:

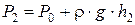, (6.32)

где r×g×h₂ – избыточное давление после расширения и установления температуры T₀,
h₂ – разность уровней жидкости в манометре после нагревания до температуры T₀.

По величине измеренных на опыте давлений P₀, P₁ и P₂ можно определить соотношение теплоемкостей:

.

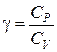Для этого мысленно выделим внутри баллона произвольную массу воздуха m₀, ограниченную замкнутой поверхностью, которая играет роль «оболочки». На рисунке 6.1 «оболочка» изображена пунктирной линией. В рассмотренных выше процессах воздух внутри нее будет расширяться и сжиматься, совершая работу против давления окружающего воздуха и обмениваясь с ним теплом.

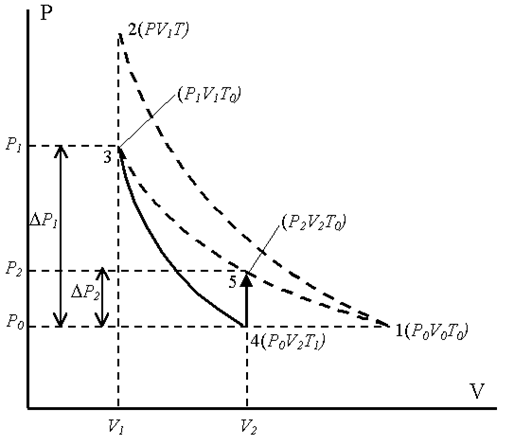
Рисунок 6.2

Запишем параметры для различных состояний воздуха внутри «оболочки».

Первое состояние – после накачки воздуха и выравнивания температур; на диаграмме P–V это точка (3) (рисунок 6.2):

I состояние – параметры – P₁, V₁, T₀.

Второе состояние точка (4) – после адиабатического расширения:

I II состояние – параметры – P₀, V₂, T₁.

Третье состояние – после закрытия крана и выравнивания температуры до T₀ – точка (5):

III состояние– параметры – P₂, V₂, T₀.

Разность давлений P₁–P₀ и P₂–P₁ в сотни и тысячи раз меньше атмосферного P₀, поэтому для упрощения вычислений с этими разностями можно обращаться как с бесконечно малыми величинами. То же относится и к соответствующим изменениям объема выделенной массы газа.

Переход газа из состояния I (3 – P₁V₁T₀) в состояние II (4 – P₀V₂T₁) происходит адиабатически:

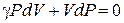. См. (6.27)

Учитывая, что в условиях опыта изменения объемов и давлений газа малы, уравнение адиабаты (6.27) можно записать:

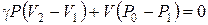. (6.33)

В состояниях I (точка 3) и III (точка 5) на диаграмме P–V воздух имеет одинаковую температуру T₀, поэтому применяем закон Бойля-Мариотта (PV = const), запишем его в дифференциальной форме:

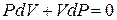
или

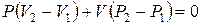. (6.34)

Решая совместно (6.33) и (6.34), имеем:

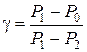. (6.35)

Подставим в это соотношение 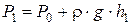и 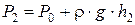получим:

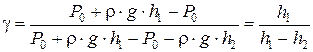. (6.37)

Так как в рабочей формуле (6.37) g выражена через отношение избыточных давлений, то измерять его можно в любых единицах. Удобнее всего выразить его в миллиметрах водяного столба по манометру.

Для определения отношения 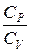опытным путем необходимо измерить разности уровней h₁ и h₂ и, пользуясь формулой (6.37), произвести вычисления.