ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА
Рассмотрим электрическую цепь, состоящую из источника тока и внешнего сопротивления (рисунок 9.2). Если замкнуть цепь, то падение потенциала распределится между внутренним и внешним участками цепи пропорционально их сопротивлениям:
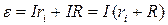 , (9.1)
, (9.1)
где 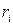 - внутреннее сопротивление источника тока;
- внутреннее сопротивление источника тока;
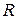 - сопротивление внешней цепи;
- сопротивление внешней цепи;
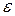 – ЭДС источника.
– ЭДС источника.
Из выражения (9.1) следует, что чем больше сопротивление внешней цепи, тем больше падение потенциала на нем. Показание вольтметра, присоединенного к полюсам источника, при разомкнутой цепи равно 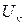 , так как при отсутствии внешней цепи сам вольтметр является нагрузкой. Если сопротивление вольтметра
, так как при отсутствии внешней цепи сам вольтметр является нагрузкой. Если сопротивление вольтметра 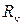 велико по сравнению с сопротивлением источника
велико по сравнению с сопротивлением источника 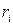 , то его показание будет приблизительно равно ЭДС источника:
, то его показание будет приблизительно равно ЭДС источника:
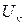 =
= 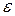 – Iri.
– Iri.
При переносе электрического заряда 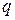 по проводнику между точками с потенциалами
по проводнику между точками с потенциалами 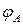 и
и 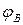 совершается работа, равная:
совершается работа, равная:
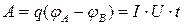 . (9.2)
. (9.2)
Мощность тока, измеряемая работой в единицу времени, будет равна:
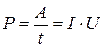 . (9.3)
. (9.3)
Из закона Ома для однородного участка цепи падение напряжения на участке цепи равно 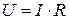 , где
, где 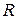 – сопротивление участка цепи. Подставляя выражение для
– сопротивление участка цепи. Подставляя выражение для 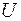 в формулу мощности, получим:
в формулу мощности, получим:
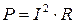 . (9.4)
. (9.4)
Полная мощность 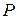 , выделяющаяся в замкнутой электрической цепи, равна сумме мощностей во внешней
, выделяющаяся в замкнутой электрической цепи, равна сумме мощностей во внешней 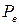 и внутренней
и внутренней 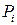 части цепи, т.е.
части цепи, т.е.
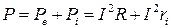 (9.5)
(9.5)
или
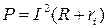 = I
= I 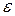 . (9.6)
. (9.6)
Полезной мощностью 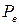 называется мощность, развиваемая на внешнем участке цепи. Она может быть найдена из уравнения:
называется мощность, развиваемая на внешнем участке цепи. Она может быть найдена из уравнения:
. (9.7)
Из уравнения (9.7) следует, что полезная мощность 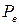 , которую можно выразить произведением
, которую можно выразить произведением 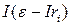 , является произведением двух сомножителей:
, является произведением двух сомножителей: 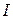 и
и 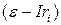 .
.
Полезная мощность может равняться нулю тогда, когда один из сомножителей равен нулю:
1) 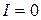 , т.е. при очень большом значении внешнего сопротивления
, т.е. при очень большом значении внешнего сопротивления
(R Þ ¥),
2) 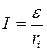 , когда внешнее сопротивление равно нулю R = 0 (короткое замыкание).
, когда внешнее сопротивление равно нулю R = 0 (короткое замыкание).
При некоторой силе тока, принимающей промежуточное значение между 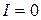 и максимальным значением силы тока
и максимальным значением силы тока 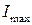 , мощность во внешней цепи максимальна. Чтобы найти силу тока, при которой полезная мощность достигает наибольшего значения, нужно взять производную по
, мощность во внешней цепи максимальна. Чтобы найти силу тока, при которой полезная мощность достигает наибольшего значения, нужно взять производную по 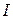 от полезной мощности, выраженной формулой (9.7), и приравнять её к нулю:
от полезной мощности, выраженной формулой (9.7), и приравнять её к нулю:
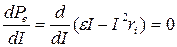 .
.
Получаем уравнение 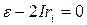 , откуда следует:
, откуда следует: 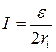 . Это отношение имеет место в том случае, когда (см. уравнение (9.1)) внешнее сопротивление цепи будет равно внутреннему сопротивлению R =ri. График зависимости
. Это отношение имеет место в том случае, когда (см. уравнение (9.1)) внешнее сопротивление цепи будет равно внутреннему сопротивлению R =ri. График зависимости 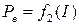 имеет вид параболы (рисунок 9.1), что следует из формулы (9.7).
имеет вид параболы (рисунок 9.1), что следует из формулы (9.7).
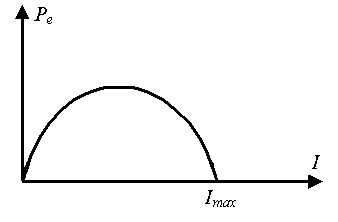
Рисунок 9.1. – График зависимости полезной мощности от тока
Так как 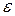 – ЭДС источника постоянна, то график зависимости полной мощности от тока представляет собой прямую, проходящую через начало координат:
– ЭДС источника постоянна, то график зависимости полной мощности от тока представляет собой прямую, проходящую через начало координат:
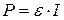 .
.
Коэффициентом полезного действия источника тока называется отношение мощности 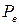 , развиваемой на внешнем участке цепи, к полной мощности
, развиваемой на внешнем участке цепи, к полной мощности 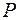 , развиваемой источником тока во всей цепи:
, развиваемой источником тока во всей цепи:
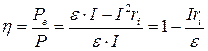 (9.8)
(9.8)
или
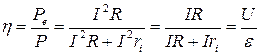 =
= 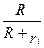 . (9.9)
. (9.9)
Формула (9.8) показывает, что КПД источника тока при постоянной ЭДС и постоянном внутреннем сопротивлении 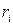 зависит только от силы тока
зависит только от силы тока 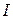 , причём эта зависимость линейная, так как
, причём эта зависимость линейная, так как 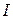 входит в формулу (9.8) в первой степени, и график зависимости
входит в формулу (9.8) в первой степени, и график зависимости 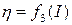 выражается прямой линией. При силе тока, близкой к нулю, т.е. при очень большом сопротивлении внешней цепи, КПД источника тока имеет наибольшее значение
выражается прямой линией. При силе тока, близкой к нулю, т.е. при очень большом сопротивлении внешней цепи, КПД источника тока имеет наибольшее значение 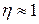 , а минимальное значение, стремящееся к нулю, – при внешнем сопротивлении, равном нулю (короткое замыкание).
, а минимальное значение, стремящееся к нулю, – при внешнем сопротивлении, равном нулю (короткое замыкание).
При. сопротивлении внешней цепи, равном внутреннему, 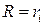 , коэффициент полезного действия будет равен 0,5 (50 %), что соответствует максимальной полезной мощности.
, коэффициент полезного действия будет равен 0,5 (50 %), что соответствует максимальной полезной мощности.
Порядок выполнения работы.В данной работе необходимо исследовать зависимости полной мощности, полезной мощности и коэффициента полезного действия источника тока от силы тока и построить графики:
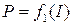 ,
, 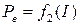 ,
, 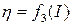 .
.
1. Для исследования указанных зависимостей необходимо собрать электрическую цепь по приведенной на рисунке 9.2 схеме.
Для искусственного увеличения внутреннего сопротивления источника тока (а значит ограничения тока при малом внешнем сопротивлении) внутри источника вмонтировано дополнительное сопротивление ri.
Максимум полезной мощности получается при равенстве сопротивления внешнего участка цепи 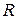 и внутреннего
и внутреннего 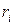 , поэтому необходимо, чтобы
, поэтому необходимо, чтобы 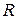 и
и 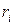 были сравнимы по порядку величины. Значение
были сравнимы по порядку величины. Значение 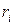 указывает преподаватель.
указывает преподаватель.
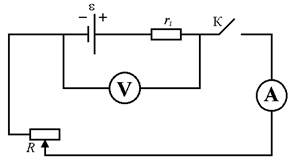
 – источник постоянного тока, К – ключ, V – вольтметр, А – амперметр,
– источник постоянного тока, К – ключ, V – вольтметр, А – амперметр,  – магазин сопротивлений,
– магазин сопротивлений,  – вмонтированное внутри источника сопротивление (или магазин сопротивлений).
– вмонтированное внутри источника сопротивление (или магазин сопротивлений).
Рисунок 9.2. – Электрическая схема установки
2. При разомкнутом ключе К записать показание вольтметра. Это показание принять за ЭДС 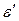 источника.
источника.
3. Замкнуть ключ К и установить на магазине такое сопротивление, чтобы ток был наибольшим. Показания амперметра и вольтметра записать.
4. С помощью магазина сопротивлений 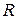 равномерно изменять ток от наибольшего до наименьшего значения таким образом, чтобы было по 5-6 значений тока и напряжения при сопротивлении внешней цепи
равномерно изменять ток от наибольшего до наименьшего значения таким образом, чтобы было по 5-6 значений тока и напряжения при сопротивлении внешней цепи 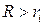 и
и 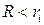 (всего 10–12 значений).
(всего 10–12 значений).
5. Разомкнуть ключ К и записать показание вольтметра 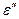 .
.
6. Вычислить среднее значение ЭДС 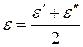 .
.
7. Вычислить для каждого значения силы тока полную и полезную мощность по формулам: 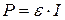 ,
, 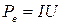 .
.
8. Вычислить коэффициент полезного действия по формуле: 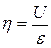 (выразить в процентах).
(выразить в процентах).
9. Заполнить таблицу 9.1.
Таблица 9.1
| № изм. | 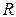 , Ом , Ом
| 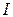 , мА , мА
| 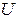 , В , В
| 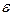 , В , В
| 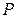 , Вт , Вт
| 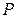 e, Вт e, Вт
| 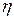 , % , %
|
| … |
10. Построить графики зависимостей 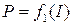 ,
, 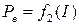 ,
, 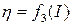 на одном рисунке. По оси абсцисс откладывать значения силы тока, по оси ординат – значения
на одном рисунке. По оси абсцисс откладывать значения силы тока, по оси ординат – значения 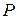 ,
, 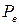 ,
, 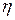 .
.
Указания. Для каждой величины 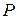 ,
, 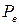 ,
, 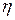 выбрать соответствующий размерам рисунка масштаб, оставляя масштаб для
выбрать соответствующий размерам рисунка масштаб, оставляя масштаб для 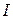 неизменным.
неизменным.
Дата добавления: 2021-02-19; просмотров: 355;











