Фильтрационный поток от нагнетательной скважины к эксплуатационной

Пусть сток О₁ и источник О₂равно дебитны, т.е. имеют одинаковые по модулю массовые дебиты G. Расстояние между источником и стоком равно 2а. Исследуем поток от источника к стоку.

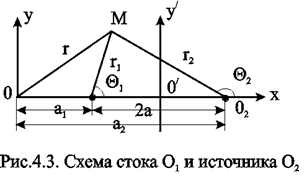
Проведём ось 0х через точки О₁ и О₂ таким образом, чтобы точка О₁находилась от начала координат 0на расстоянии а₁, а точка О₂на расстоянии а₂(рис. 4.3).

По формуле (4.2) определим потенциальную функцию потока. При этом учтем знаки дебитов: источник G ₁= - G, а сток G ₂= + G. После подстановки получим:

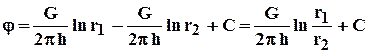, (4.5)

где r₁ и r₂- расстояния любой точки пласта до стока и источника, соответственно.

Уравнение изобар (4.4) при этом будет иметь вид

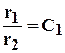(4.6)

и соответствует окружностям, центры которых расположены на оси 0х. Если поместим начало координат в центре какой-либо окружности семейства, то радиус данной окружности определится выражением

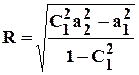, (4.7)

а коэффициент 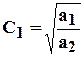. (4.8)

Подставляя С₁в (4.7) найдем

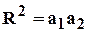. (4.9)

Из (4.9) видно, что a₁ < R < a₂или a₁ > R > a₂; следовательно, все окружности пересекают ось между стоком и источником, а значит, одна из особых точек находится внутри окружности данного радиуса R, другая - вне этой окружности. Точки О₁ и О₂, положения которых на прямой 0х определяются равенством (4.7), называются взаимо-симметричными относительно окружности радиуса R.

Допустим, что радиус R=¥,т.е. берём ту эквипотенциальную линию, которая является прямой. Из (4.7) следует, что в этом случае С₁=1 и, как следует из (4.6), r₁=r₂ . Последнее равенство означает, что в числе эквипотенциальных линий есть прямая 0у^,, которая делит расстояние между стоком и источником пополам и параллельна оси 0у (рис.4.3).

Итак, эквипотенциальные линии (изобары) при совместном действии одной эксплуатационной и одной нагнетательной скважин в неограниченном пласте представляют собой окружности, центры которых расположены на прямой, проходящей через центры скважин (рис.4.4).. Среди окружностей есть одна, имеющая бесконечно большой радиус - прямая, которая делит расстояние между скважинами и всю плоскость течения пополам. Половина всех окружностей конечного радиуса Rрасположена по одну сторону от этой прямой, остальные окружности - по другую.

Семейство линий тока ортогонально изобарам и, следовательно, в данном случае тоже окружности. Все линии тока проходят через сток и источник. Центры всех окружностей линий тока расположены на прямой, делящей расстояние между стоком и источником пополам (рис.4.4).

Решая, полученную систему уравнений, имеем

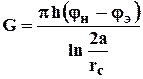. (4.10)

Массовая скорость фильтрации в любой точке пласта М (рис.4.2) находится по правилу суперпозиции сложения векторов скорости от действия источника и стока

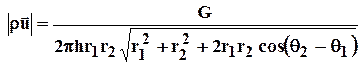. (4.11)

Величина корня есть расстояние между источником и стоком 2аи, следовательно, формула (4.11) перепишется в виде

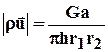(4.12)

Для поддержания пластового давления часто используется нагнетание воды в пласт. Определим время движения частицы по кратчайшему пути между нагнетательной и эксплуатационной скважинами для однородной несжимаемой жидкости, т.е. по оси 0х. При жестководонапорном режиме решается при этом вопрос о времени, протекшем от начала закачки воды в пласт до начала её прорыва в эксплуатационную скважину.

Чтобы решить указанную задачу выразим скорость в (4.12) через производную расстояния по времени и, поместив начало координат в сток О₁, проинтегрируем полученное уравнение по хот х₀до х. Тогда время движения частицы от некоторой точки х₀до точки х определится зависимостью

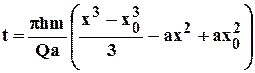. (4.13)

Время обводнения Т, т.е. прохождения частицы расстояния О₁О₂ = 2а определится из (4.13), если принять х=0; х₀=2а

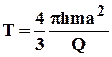, (4.14)

где m - пористость;Q- объёмный дебит.

Зная Т можно найти площадь обводнения w, приравнивая объёмы TQи mhw. Откуда

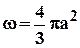. (4.15)

Анализ формул (4.13) и (4.14) показывает, что расстояние, пройденное частицей за время Тот нагнетательной скважины до эксплуатационной, вдвое больше расстояния пройденного другой частицей за это же время в положительном направлении оси х.