Однородная несжимаемая жидкость в деформируемом (трещиноватом) пласте

Для трещиноватой среды двухчленный закон записывается в виде

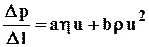, (1.46)

где 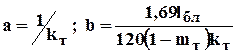; l_бл- средний линейный размер блока.

Умножим все члены (1.46) на плотность rи вынесем за скобки вязкость h. Тогда применительно к плоскорадиальному потоку получим:

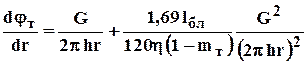, (3.54)

где .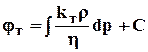

После разделения переменных и интегрирования (3.54) в пределах r_c - r_к ; j_с - j_к получим

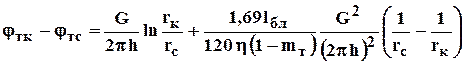, (3.56)

Если в (3.56) подставим выражение для трещинной проницаемости и выразим массовый дебит через объёмный, то будем иметь окончательное выражение

(3.56*)

Как видно из (3.56*), индикаторная кривая в этом случае определяется в результате сложения двух парабол - параболы четвёртого порядка, симметричной относительно оси, параллельной оси дебитов, и параболы второго порядка (относительно дебита Q) симметричной относительно оси, параллельной оси депрессий (Dр_с) и отстоящей от последней на расстоянии, равном

.

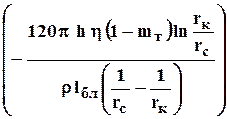3.2.5.4. Идеальный газ в деформируемом (трещиноватом) пласте

Из (3.56*) при подстановке выражений для плотности, проницаемости и приведённого к стандартным условиям объёмного дебита можно получить следующее выражение

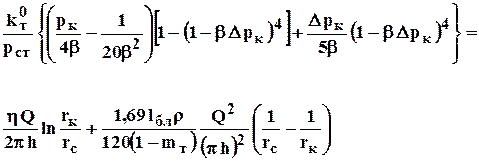. (3.57)