Уравнения потенциального движения

Потенциальным течением будем называть течение, при котором проекции массовой скорости на оси ортогональной системы координат будут являться производными некоторой функции по направлениям данных осей.

Фильтрационное течение в горных породах подчиняется закону Дарси и, следовательно, потенциально. Потенциалом поля скоростей фильтрационного течения называется функция

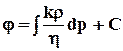. (2.5)

Равенство (2.5) можно переписать в виде

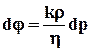(2.6)

или, учитывая закон Дарси,

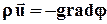. (2.7)

Здесь r`u - вектор массовой скорости фильтрации;

gradj- градиент потенциала j, направленный в сторону быстрейшего возрастания j,

;

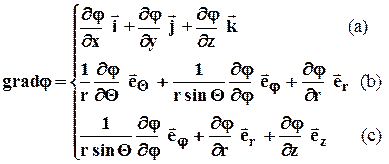(a)- декартовые координаты; (b) - сферические координаты; (c) - цилиндрические координаты;

i, j, k , e_Q , e_j , e_r , e_z - единичные вектора по осям координат x, y, z , Q, j, r и z (цилиндрическая система ).

Подставляя (2.7)в (2.1) 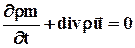получим

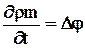, (2.8)

а для установившегося течения

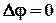. (2.9)

Уравнения (2.8) и (2.9) называют уравнениями Лапласа относительно функции j, а оператор Dj оператором Лапласа.

Уравнение Лапласа имеет два важных свойства, которые имеют большое практическое приложение, а именно:

1. сумма частных решений является также решением уравнения Лапласа;

2. произведение частного решения на константу - также решение.

Данные свойства приводят к принципу суперпозиции.

В скалярной форме оператор Лапласа имеет вид

;

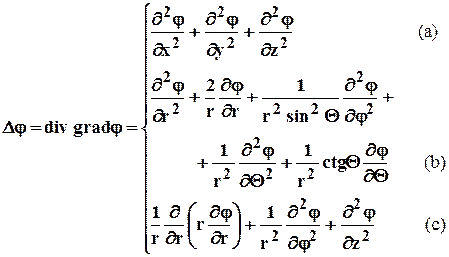где: (a) - декартовые координаты; (b) - сферические координаты; (c) - цилиндрические координаты.