Общая система уравнений

В чисто трещиноватом пласте система уравнений имеет тот же вид, что и в пористом. Для трещиновато-пористой среды следует учитывать характерные особенности такой среды (рис.1.2):

1) такой пласт моделируется системой двух сред с порами разных масштабов (среда 1 - роль поровых каналов играют трещины, а роль зёрен - пористые блоки; среда 2 - обычная пористая среда, образующая блоки);

2) между отмеченными средами при фильтрации возникает переток жидкости из пористых блоков в трещины в пределах выделенного элементарного объёма трещиновато-пористого пласта.

При этом предполагается, что в каждом элементарном объёме трещиновато-пористого пласта содержится большое число пористых блоков, так что в окрестности каждой точки вводится две скорости фильтрации, два давления, относящиеся к средам 1 и 2. На основании сказанного, уравнения неразрывности выписываются для каждой из сред, а переток учитывается членом q_1,2. Наличие перетока эквивалентно существованию внутренних источников жидкости в выделенном объёме.

Для жидкости, находящейся в трещинах, имеем

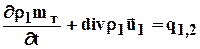. (2.10)

Для жидкости в пористых блоках

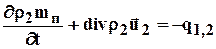. (2.11)

Здесь q_1,2 - масса жидкости, поступающей из пористых блоков в трещины за единицу времени на единицу объёма с размерностью МL^-3T^-1.

Будем полагать, что q_1,2 пропорционально разности фильтрационных потенциалов первой и второй сред

q_1,2=Q (j₂ - j₁), (2.12)

где Q - коэффициент переноса, размерности L^-2.

Для чисто трещиноватого пласта считаем q_1,2=0 и тогда будем иметь только одно уравнение неразрывности для жидкости в системе трещин (в пористых блоках не содержится жидкость). При установившейся фильтрации жидкости в трещиновато-пористом пласте, когда во всём пласте существует только одно давление р₁=р₂=р получаем

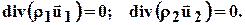(2.13)

Для чисто трещинного пласта

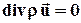. (2.14)