Границы применимости закона Дарси

Закон Дарси справедлив при соблюдении следующих условий:

a) пористая среда мелкозерниста и поровые каналы достаточно узки;

b) скорость фильтрации и градиент давления малы;

с) изменение скорости фильтрации и градиента давления малы.

При повышении скорости движения жидкости закон Дарси нарушается из-за увеличения потерь давления на эффекты, связанные с инерционными силами: образование вихрей, зон срыва потока с поверхности частиц, гидравлический удар о частицы и т.д. Это так называемая верхняя граница. Закон Дарси может нарушаться и при очень малых скоростях фильтрации в процессе начала движения жидкости из-за проявления неньютоновских реологических свойств жидкости и её взаимодействия с твёрдым скелетом пористой среды. Это нижняя граница.

Верхняя граница. Критерием верхней границы справедливости закона Дарси обычно служит сопоставление числа РейнольдсаRe=war/h с его критическим значением Re_кр, после которого линейная связь между потерей напора и расходом нарушается. В выражении для числа Re:

w-характерная скорость течения:

а - характерный геометрический размер пористой среды;

r - плотность жидкости.

Имеется ряд представлений чисел Рейнольдса, полученных различными авторами при том или ином обосновании характерных параметров. Приведём некоторые из данных зависимостей наиболее употребляемые в подземной гидромеханике:

а) Павловского

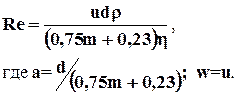(1.30)

Критическое число РейнольдсаRe_кр=7,5-9.

б) Щелкачёва

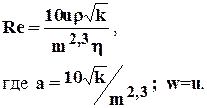(1.31)

Критическое число Рейнольдса Re_кр=1-12.

в) Миллионщикова

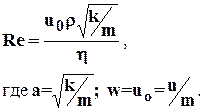(1.32)

Критическое число Рейнольдса Re_кр=0,022-0,29.

Скорость фильтрации u_кр, при которой нарушается закон Дарси, называется критической скоростью фильтрации. Нарушение скорости фильтрации не означает перехода от ламинарного движения к турбулентному, а вызвано тем, что силы инерции, возникающие в жидкости за счёт извилистости каналов и изменения площади сечения, становятся при u>u_кр соизмеримы с силами трения.

При обработке экспериментальных данных для определения критической скорости пользуются безразмерным параметром Дарси:

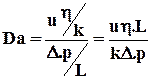, (1.33)

представляющим отношение сил вязкого трения к силе давления. В области действия закона Дарси данный параметр равен 1 и уменьшается при превышении числа Re критического значения.

Нижняя граница. При очень малых скоростях с ростом градиента давления (изменение давления с глубиной) увеличение скорости фильтрации происходит более быстро, чем по закону Дарси. Данное явление объясняется тем, что при малых скоростях становится существенным силовое взаимодействие между твердым скелетом и жидкостью за счет образования аномальных, неньютоновских систем, н.п. устойчивые коллоидные растворы в виде студнеобразных плёнок, перекрывающих поры и разрушающихся при некотором градиенте давленияt_н , называемого начальным и зависящим от доли глинистого материала и величины остаточной водонасыщенности. Имеется много реологических моделей неньютоновских жидкостей, наиболее простой их них является модель с предельным градиентом

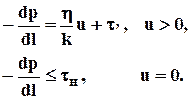(1.34)

1.3.1.4. Законы фильтрации при Re > Re_кр

От точности используемого закона фильтрации зависит достоверность данных исследования скважин и определение параметров пласта. В связи с этим в области нарушения действия закона Дарси необходимо введение более общих, нелинейных законов фильтрации. Данные законы разделяются на одночленные и двухчленные.

Одночленные законы описываются степенной зависимостью вида

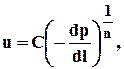(1.35)

где C, n - постоянные, 1£ n £ 2.

Данные зависимости не удобны, т.к. параметр nв общем случае зависит от скорости фильтрации. В связи с этим наибольшее употребление нашли двухчленные зависимости, дающие плавный переход от закона Дарси к квадратичному, называемому формулой Краснопольского:

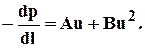(1.36)

КоэффициентыА и Вопределяются либо экспериментально, либо теоретически. В последнем случае

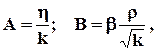(1.37)

где b - структурный коэффициент и по Минскому определяется выражением

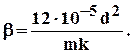
Трещиноватая среда

<3 4 567 8 9 >

Дата добавления: 2016-11-29; просмотров: 3205;