Стехиометрические расчеты
Все количественные соотношения при расчете химических процессов основаны на стехиометрии реакций. Количество вещества при таких расчетах удобнее выражать в молях, или производных единицах (кмоль, ммоль, смоль и т. д.). Моль является одной из основных единиц СИ. Один моль любого вещества соответствует его количеству, численно равному молекулярной массе. Поэтому молекулярную массу в этом случае следует считать величиной размерной с единицами: г/моль, кг/кмоль, кг/моль. Так, например, молекулярная масса азота 28 г/моль, 28 кг/кмоль, но, однако, 0,028 кг/моль.
Массовые и мольные количества вещества связаны известными соотношениями
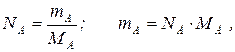
где NA – количество компонента А, моль;
mA – масса этого компонента, кг;
MА – его молекулярная масса, кг/моль.
При непрерывных процессах поток вещества А можно выражать его мольным количеством в единицу времени
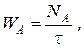
где WA – мольный поток компонента А, моль/с;
t -время, с.
Для простой реакции, протекающей практически необратимо, обычно стехиометрическое уравнение записывается в виде
nAA+nBB=nRR+nSS.
Однако удобнее записывать стехиометрическое уравнение в виде алгебраического, принимая при этом, что стехиометрические коэффициенты реагентов – отрицательны, а продуктов реакции – положительны:
-nAA-nBB + nRR + nSS = 0.
Тогда для каждой простой реакции можно записать следующие равенства:
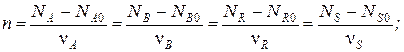
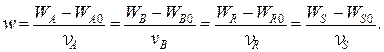
Индекс «0» относится к начальному количеству компонента.
Эти равенства дают основание получить следующие уравнения материального баланса по компоненту для простой реакции:

Пример 7.1. Реакция гидрирования фенола до циклогексанола протекает по уравнению
С6H5OH + 3H2 = C6H11OH, или A + 3B = R.
Вычислить количество образовавшегося продукта, если начальное количество компонента А было 235 кг, а конечное – 18,8 кг.
Решение: Запишем реакцию в виде R – A – 3B = 0. Молекулярные массы компонентов: MA = 94 кг/кмоль, MB = 2кг/кмоль и MR = 100 кг/кмоль. Тогда мольные количества фенола в начале и в конце реакции будут:
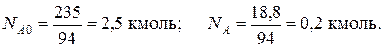
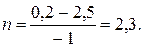
Количество образовавшегося циклогексанола будет равно
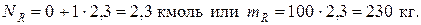
Определение стехиометрически независимых реакций в их системе при материальных и тепловых расчетах реакционных аппаратов необходимо для исключения реакций, являющихся суммой или разностью некоторых из них. Такую оценку наиболее просто можно осуществить по критерию Грама.
Чтобы не проводить излишних расчетов, следует оценить, является ли система стехиометрически зависимой. Для этих целей необходимо:
- транспонировать исходную матрицу системы реакций;
- умножить исходную матрицу на транспонированную;
- вычислить определитель полученной квадратной матрицы.
Если этот определитель равен нулю, то система реакций стехиометрически зависима.
Пример 7.2. [76] Имеем систему реакций:
FeO + H2 = Fe + H2O;
Fe2 O3+ 3H2 = 2Fe + 3H2O;
FeO + Fe 2O3 + 4H2 = 3Fe + 4H2O.
Эта система стехиометрически зависима, так как третья реакция является суммой двух других. Составим матрицу
| FeO | Fe2O3 | H2 | Fe | H2O |
| -1 | -1 | |||
| -1 | -3 | |||
| -1 | -1 | -4 |
Определитель равен нулю. При отбрасывании третьей реакции определитель равен 28, т. е. две первых реакции стехиометрически независимы.
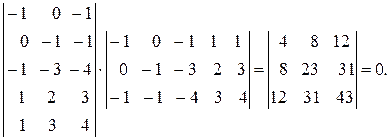
Для удаления стехиометрически зависимых реакций в системе необходимо составить матрицу системы. Допустим для системы реакций:
4NH3 + 5O2 = 4NO + 6H2O;
4NH3 + 3O2 = 6H2O + 2N2;
4NH3 + 6H2O = 5N2 + 6H2O;
O2 + 2NO = 2NO2;
2NO = O2 + N2;
2O2 + N2 = 2NO2
можно составить матрицу:
| NH3 | O2 | NO | H2O | N2 | NO2 |
| -4 | -5 | ||||
| -4 | -3 | ||||
| -4 | -6 | ||||
| -1 | -2 | ||||
| -2 | |||||
| -2 | -1 |
По сути, к данной матрице следует применить преобразование Гаусса. Заменим вторую и третью строку их разностями с первой и умножим на 2 и разделим на 5 третью строку, которую вычтем из второй. Затем умножим четвертую и пятую строку на 2 и вычтем их из второй:
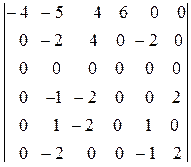
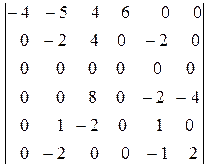 .
.
Умножим пятую строку на -2 и вычтем ее из второй, а также вычтем из второй строки шестую. Умножив затем шестую строку на 2 и вычитая ее из четвертой, получим окончательно
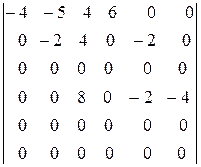
Отсюда видно, что третья, пятая и шестая реакции являются стехиометрически зависимыми. Окончательно система примет вид, если для простоты расчетов подставить вместо полученной четвертой реакции ее разность со второй
4NH3 + 5O2 = 4NO + 6H2O;
2NO = N2 + O2;
2NO + O2 = 2NO2.
ПРИМЕР 7.3. Определение линейно независимых реакций на примере растворения никеля в серной кислоте
Для процесса растворения металлического никеля в серной кислоте можно записать следующие возможные уравнения реакции в равновесной системе:
Ni + 2H2SO4 ↔ NiSO4 + SO2 + 2H2O (1)
Ni + H2SO4 ↔ NiSO4 + H2 (2)
3Ni + 4H2SO4 ↔ 3NiSO4 + S + 4H2O (3)
4Ni + 5H2SO4 ↔ 4NiSO4 + H2S + 4H2O (4)
2Ni + 3H2SO4 ↔ 2NiSO4 + H2 + SO2 + 2H2O (5)
Как показано [69] число независимых реакций равно числу веществ (Ni, H2SO4, NiSO4, H2O, SO2, H2, S, H2S) в системе минус число разнородных атомов (Ni, H2, S, O2), из которых образованы реагенты,
т. е. для уравнений (1–5) число независимых реакций равно четырем
(8–4=4).
Обозначим:
А1 = Ni, А2= H2SO4., А3 = NiSO4, А4 = SO2,
А5 = H2O, А6 = H2S, А7 = H2, А8 = S.
Запишем четыре уравнения реакций (1, 2, 3, 5) в виде системы следующих однородных алгебраических уравнений:
–А1 – 2A2 + A3 + A4 + 2A5 + 0 + 0 + 0 = 0
–А1 – А2 + А3 + 0 + 0 + 0 + А7 + 0 = 0
–3А1 – 4А2 + 3А3 + 0 + 4А5 + 0 + 0 + А8 = 0
–2А1 – 3А2 + 2А3 + А4 + 2А5 + 0 + А7 + 0 = 0
Векторами уравнений рассматриваемых реакций будут
а1 (-1, -2, +1, +1, +2, 0, 0, 0)
а2 (-1, -1, +1, 0, 0, 0, +1, 0)
а3 (-3, -4, +3, 0, +4, 0, 0, +1)
а4 (-2, -3, +2, +1, +2, 0, +1, 0)
Составим скалярные произведения
а1а1 = 11, а1а2 = 4, а1а3 = 22, а1а4 = 15
а2а2 = 4, а3а3 = 51, а4а4 = 23, а2а4 = 8,
а3а4 = 32, а3а2 = 10.
Для проверки линейной независимости реакций можно использовать определитель Грама, являющийся квадратом смешанного (векторно-скалярного) произведения векторов:
| [а1а2 … а]2= | а1а1 а1а2 а1а3 а1а |
| а2а1 а2а2 а2а3 а2а | |
| . . . . . . . . . . | |
| а а1 а а2 а а3 а а |
Находим определитель Грама для уравнений реакций (1, 2, 3, 5)
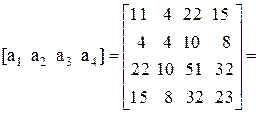 11А+4В+22С+15D=0,
11А+4В+22С+15D=0,
где
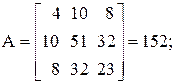
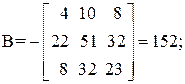
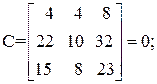 .
. 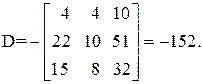
Определитель Грама равен нулю. Следовательно, система уравнений реакций (1, 2, 3, 5) является линейно зависимой.
Пусть имеем систему реакций протекающих по уравнениям (1-4). Запишем уравнения реакций (1-4) также в виде системы однородных алгебраических уравнений:
-А1 – 2A2 + A3 + A4 +2A5 + 0 + 0 + 0 = 0
-А1 – А2 + А3 + 0 + 0 + 0 + А7 + 0 = 0
-3А1 – 4А2 + 3А3 + 0 + 4А5 + 0 + 0 + А8= 0
-4А1 – 5А2 + 4А3 + 0 + 4А5 + А6+ 0 + 0 = 0
Векторами уравнений рассматриваемых реакций будут:
а1 (-1, -2, +1, +1, +2, 0, 0, 0)
а2 (-1, -1, +1, 0, 0, 0, +1, 0)
а3 (-3, -4, +3, 0, +4, 0, 0, +1)
а4 (-4, -5, +4, 0, +4, +1, 0, 0)
Скалярные произведения равны:
а1а1=11, а1а2=4, а1а3=22, а1а4=26.
а2а2=4, а3а3=51, а4а4=74, а2а3=10,
а2а4=13, а3а4=60
Находим определитель Грама:
| [а1а2 … а]2 = | 11 4 22 26 | = 11А + 4В + 22С + 26D=395 |
| 4 4 10 13 | ||
| 22 10 51 60 | ||
| 26 13 60 74 |
где
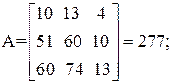
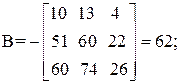
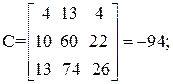
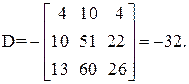
Так как определитель Грама не равен нулю, то уравнения реакций (1–4) являются линейно независимыми.
Одновременно с числом стехиометрически независимых реакций определяется равное ему число ключевых веществ, по которым можно составить материальный баланс реакций. В простой реакции ключевое вещество одно. В сложных реакциях выбор независимых реакций и ключевых веществ взаимосвязан и определяется тем, чтобы в каждой независимой реакции участвовало хотя бы одно ключевое вещество и, кроме того, выбранные ключевые вещества участвовали бы в одной или в некотором минимуме реакций. Так, в предыдущем примере в качестве ключевых можно выбрать аммиак, азот и диоксид азота.
Для каждой из независимых реакций можно записать:
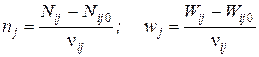 ;
;

Здесь i – индекс, соответствующий веществу, а j – индекс, соответствующий номеру реакции.
Дата добавления: 2021-02-19; просмотров: 583;











