Динамические и аэродинамические расчеты висячих и вантовых мостов
Причины и цель динамических и аэродинамических
расчетов висячих и вантовых мостов
В обычных конструкциях мостов динамическая и ветровая нагрузки играют второстепенную роль. Что касается висячих и вантовых мостов больших пролетов, то их влияние на прочность и надежность сооружения велико.
Висячие и вантовые мосты испытывают значительные колебания, вызываемые действием вертикальных и горизонтальных нагрузок, особенно периодически изменяющихся во времени. Это обусловлено большой протяженностью и гибкостью данных сооружений, малым собственным весом, неблагоприятными динамическими свойствами (низкие частоты и малые значения логарифмических декрементов колебаний), неблагоприятными аэродинамическими и сейсмическими условиями (районы строительства, как правило, горные или открытые морские заливы).
Методы динамического и аэродинамического расчета очень сложны и еще недостаточно разработаны. Это объясняется сложностью происходящих в пролетных строениях процессов, большим разнообразием конструктивных форм, необходимостью решения громоздких систем нелинейных уравнений, многие коэффициенты которых известны лишь приближенно и не поддаются строгому теоретическому обоснованию.
Поэтому при строительстве крупных мостов проводят исследования проектируемой конструкции на модели, подвергаемой действию пульсирующих вертикальных и горизонтальных нагрузок и воздушного потока в аэродинамической трубе. Основная цель динамических расчетов и экспериментов состоит в нахождении таких геометрических и жесткостных характеристик пролетного строения, при которых исключается возможность развития опасных колебаний сооружения при эксплуатации.
Исторически в развитии проектирования висячих и вантовых мостов выделяют три этапа. На первом первостепенным считалось обеспечение статической прочности сооружения. Динамическая и аэродинамическая устойчивость при этом обеспечивалась совершенно случайно. Второй этап начался с крушения Такомского моста в 1940 г. Этот период характерен повышением внимания к вопросам динамической и аэродинамической устойчивости мостов. Третий этап - это последние 15-20 лет, когда динамика и аэродинамика инженерных сооружений сформировались в самостоятельные научные направления. Подробнее с последними достижениями в этой области можно ознакомиться в [Проектирование металлических мостов / Под ред. А.А. Петропавловского. М.: Транспорт, 1982. 320 с., Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.].
Основы динамического расчета. Причины и виды колебаний
висячих и вантовых мостов
Каждое тело (конструкция) может колебаться по многим формам колебаний, которые характеризуются числом полуволн i (рис. 14.1). Формы колебаний при i £ 3 называются основными. Каждое тело обладает числом степеней свободы n, т.е. числом координат, которыми можно описать положение конструкции в любое время (рис. 14.2). Реальные мосты обладают бесконечным числом степеней свободы (n®¥). Каждое тело может испытывать свободные колебания, т.е. колебания, которые возникают при выведении данного тела из состояния равновесия или покоя.
Свободные колебания реальных сооружений с n степенями свободы представляют собой набор из происходящих одновременно собственных колебаний, каждое из которых имеет определенную частоту wi и форму колебаний (i = 1, 2, 3, ...).
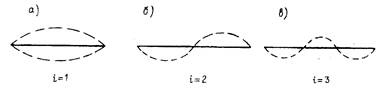
Рис. 14.1. Основные формы колебаний
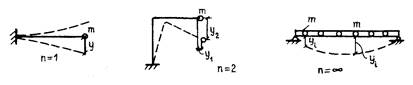
Рис. 14.2. Число степеней свободы
Круговая частота (w - число колебаний за 2p с, 1/с) и период (Т - время одного полного колебания, с) связаны между собой (рис. 14.3, а):
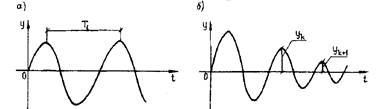
Рис. 14.3. Свободные (а) и затухающие (б) колебания
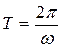 и
и 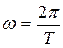 . (14.1)
. (14.1)
Для динамического расчета реальных сооружений с n степенями свободы наибольшее значение имеют частоты собственных колебаний, которые, располагаясь в порядке возрастания, образуют спектр собственных частот (w1, w2, w3,...,wn).
За счет внутреннего и внешнего сопротивления практически все колебания в природе - затухающие (рис. 14.3, б). Количественная характеристика скорости этого процесса называется логарифмическим декрементом колебаний:
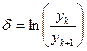 . (14.2)
. (14.2)
Для железобетонных мостов d » 0,3, для металлических d » 0,1, для висячих и вантовых d » 0,015...0,07.
Вынужденные колебания возникают под воздействием различных сил, имеющих свою частоту q. При совпадении частоты возмущающей силы q и частоты свободных колебаний конструкции w наступает явление резонанса, т.е. резкое увеличение амплитуды колебаний, а следовательно, возрастание деформаций и напряжений, что недопустимо при нормальной эксплуатации сооружения.
Причины и виды колебаний мостов. Пролетные строения могут испытывать вертикальные, горизонтальные и крутильные колебания.
Возникновение колебаний в вертикальной плоскости вызывается динамическим воздействием подвижной временной нагрузки, которая является по отношению к мосту переменной. Причины этих колебаний:
- неровности проезжей части, что при движении транспорта приводит к толчкам, ударам;
- колебания отдельных неуравновешенных частей подвижного состава (колебания кузова на рессорах, подрессорных частей на пневматических шинах);
- ритмическое воздействие гусеничной нагрузки за счет ударов звеньев;
- ритмическое воздействие от пешеходов, особенно идущих в ногу.
Колебания в горизонтальной плоскости могут возникнуть от воздействия ветра, если его порывы будут чередоваться с определенным интервалом.
Крутильные колебания пролетного строения возникают от несимметричного приложения вертикальных и горизонтальных нагрузок.
Учет динамического воздействия подвижной нагрузки
при расчете висячих и вантовых мостов
Согласно требованиям СНиП 2.05.03-84 учет динамического воздействия подвижной нагрузки проводится при помощи динамического коэффициента 1+m, величина которого для конструкции висячих и вантовых мостов равна:
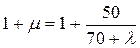 . (14.3)
. (14.3)
Кроме того, нормы предусматривают оценку сооружения по периодам собственных колебаний с целью исключения резонансных явлений. На основании опытных данных по динамическим характеристикам подвижного состава (поездов, автомобилей) и пешеходов техническими нормами устанавливаются резонансные зоны, появления которых следует избегать при проектировании (п. 1.48):
- для железнодорожных мостов
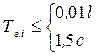 , (14.4)
, (14.4)
- для автодорожных и пешеходных мостов
Тв,i ¹ (0,45...0,6) с; (14.5)
Тг,i ¹ (0,9 ... 1,2) с, (14.6)
где l - длина пролета; Тг,i и Тв,i - соответственно периоды горизонтальных и вертикальных колебаний i-й формы.
Для висячих мостов необходимо также выполнить проверку на возникновение «параметрического резонанса» [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]. Это явление, связанное с нелинейными деформациями висячей системы, получило еще название «перекачки энергии» вследствие того, что происходит процесс перехода вертикальных колебаний в горизонтальные и наоборот. Параметрический резонанс наступает при совпадении периода горизонтальных колебаний моста Тг,i с периодом вертикальных колебаний Тв,i или при кратности их друг другу (рис. 14.4), поэтому:
Тг,i ¹ Тв,iK , где К = 1, 2, 3 ... или 1/2, 1/3, 1/4,... (14.7)
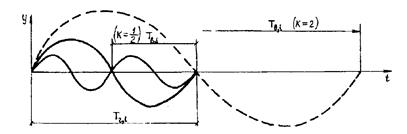
Рис. 14.4. Параметрический резонанс висячих мостов
Как видно из формул (14.4-14.7), задача динамического расчета конструкций сводится к определению динамических характеристик пролетного строения w и Тi, по величине которых и дается оценка пригодности сооружения к эксплуатации.
Динамические характеристики висячих и вантовых мостов
Динамические характеристики для висячих и вантовых мостовопределяются так же, как для других систем, путем решения дифференциальных уравнений колебаний при помощи аналитических или численных методов [Смирнов В.А. Висячие мосты больших пролетов. 2-е изд., перераб. и доп. М.: Высш. школа, 1975. 368 с., Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с., Кушнерев А.М. Проектирование и расчет висячих и вантовых мостов. Новосибирск, 1969. 102 с., Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.]. Эти уравнения составлены таким образом, что после их решения обычно находятся величины wi, хотя в формулах СНиПа регламентируются значения Тi (4.4-4.7).
Для сравнения приведем формулу определения собственных частот для балки на двух опорах [Лазарев И.Б. Основы устойчивости и динамики сооружений: Учеб. пособие. Новосибирск, 1987. 83 с.]:
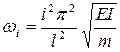 , (15.1)
, (15.1)
где i - номер формы колебания, i £ 3; EI, l - изгибная жесткость и пролет балки; m - масса 1 м пролетного строения, т/м.
Частота вертикальных колебаний висячих мостов системы «нить-балка» (см. рис. 1.1) определяется по приближенной формуле [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]:
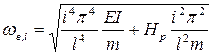 , (15.2)
, (15.2)
где Hp - распор от постоянной нагрузки, i =2, 4, 6, ...
Для i =1, 3, 5, ... частота wв,i зависит от осевой жесткости кабеля, поэтому вычисляется по формуле (15.2), но с добавлением в подкоренное выражение третьего слагаемого Z0 [Смирнов В.А. Висячие мосты больших пролетов. 2-е изд., перераб. и доп. М.: Высш. школа, 1975. 368 с.]:
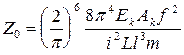 . (15.3)
. (15.3)
Для висячих систем повышенной жесткости величины wв,1, wв,3 рассчитывают по формулам (15.2), (15.3), а для i = 2 величину wв,2 нужно увеличить в 1,25-1,4 раза [Кирсанов Н.М. Расчет висячих комбинированных систем по линиям влияния с учетом прогибов. Воронеж, 1976. 103 с.]. Это объясняется тем, что данные конструкции имеют прогибы в 1,15-1,2 раза меньше при загружении полупролета, чем обычная система «нить-балка».
Частота вертикальных собственных колебаний двухпролетных вантовых мостов определяется по формуле [Смирнов В.А. Висячие мосты больших пролетов. 2-е изд., перераб. и доп. М.: Высш. школа, 1975. 368 с.]:
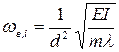 , (15.4)
, (15.4)
где li - характеристические числа, зависящие от формы колебаний i: l1 =3,527; l2 = 0,342; l3 = 0,15.
Частота аналогичных колебаний трехпролетных вантовых мостов вычисляется по формуле [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]:
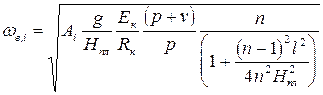 , (15.5)
, (15.5)
где n - число панелей в среднем пролете, Ai - коэффициент, А1= 0,35, A2 = 1,25.
Частота горизонтальных колебаний для всех систем висячих и вантовых мостов зависит только от жесткости пролетного строения в горизонтальной плоскости и высоты подвеса балки жесткости к пилону, ее можно определить по формуле [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]
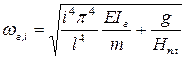 , (15.6)
, (15.6)
где Iг - момент инерции балки жесткости в горизонтальной плоскости, обычно он больше I в десятки раз.
Если не выполняются проверки (14.4-14.7), следует откорректировать размеры поперечных сечений балки жесткости или кабеля в сторону увеличения, так как ранее они были подобраны из условия жесткости и прочности. Величина изменения ЕI, ЕIг, Еk, Аk определяется на основе анализа формул (15.2-15.6), и требуемый результат получается путем нескольких пробных попыток расчета.
Специальные меры для гашения колебаний в висячих и вантовых мостах
Конструктивные меры:
- применение многовантовых систем, где каждая ванта имеет свое значение wi и колебания вант гасят друг друга;
- использование железобетона для балки жесткости или пилона (повышается d);
- применение А-образных пилонов.
Устройство демпферов (виброгасителей).
На рис. 15.1 показаны демпферы для вант и балок жесткости в виде изгибаемых пластинок. При возникновении колебаний ванты устройство, приведенное на рис. 15.1, а, будет гасить эти колебания за счет того, что собственная частота двух его противовесов на коротком канате отличается от аналогичной частоты ванты. Демпфер, показанный на рис. 15.1, б, будет препятствовать развитию горизонтальных колебаний пролетного строения за счет соединения балки жесткости с массивной опорой при помощи металлической пластинки. Данные устройства весьма эффективны при защите мостов от сейсмических воздействий. Более подробно этот вопрос освещен в [Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.].
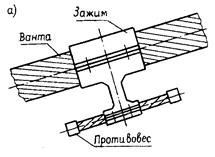
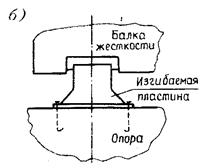
Рис. 15.1. Демпфирующие устройства
Основы аэродинамического расчета висячих и вантовых мостов
Постановка проблемы
Под термином «аэродинамическая устойчивость» понимается способность висячих и вантовых мостов противостоять воздействиям ветра. Как отмечалось, данная проблема вышла на передний план в 1940 г., когда при относительно небольшой скорости ветра (v = 19 м/с) за 1 ч разрушился висячий мост через р. Такома пролетом 855 м. Такомская катастрофа выявила, что были недостаточными проверки конструкции на прочность, жесткость, динамическую устойчивость.
Появилось новое направление в науке - аэродинамика висячих и вантовых мостов, которое охватывает аэромеханику (изучение сил, действующих при взаимодействии конструкции с ветровым потоком) [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.].
Достижения в области аэродинамики широко используются в самолетостроении. Но попытки перенести авиационные методы и принципы на висячие и вантовые мосты не принесли успеха.
В авиации перед аэродинамикой ставятся другие, более ясные цели: найти форму конструкции, которая давала бы максимальную скорость движения, минимальное сопротивление движению и максимальную подъемную силу. Для мостов несколько другие цели - здесь, наоборот, не нужны ни подъемная сила, ни скорость движения, единственное, что совпадает, - это требование улучшенной обтекаемости моста потоком воздуха.
В авиации конструкции самолетов аналогичны друг другу и функционируют практически в одинаковых условиях. У мостов большое многообразие форм, геометрических и жесткостных характеристик, в целом неблагоприятных для обтекания воздухом, так как эти конструкции формируются из соображений, прежде всего связанных с обеспечением пропуска нагрузки, жесткости и прочности. Кроме того, каждый мост имеет свои климатические и аэровоздушные условия.
Что касается экспериментов, то и здесь авиация имеет преимущества: самолет можно испытать в аэродинамической трубе и на пульсаторе целиком и в натуральную величину. Любые затраты на экспериментальные исследования окупятся, так как самолеты выпускаются серийно. Для мостов можно устроить испытание только на модели или на части конструкции в натуральную величину, а главное, каждый мост индивидуален.
Несмотря на перечисленные трудности, в области аэродинамики мостов многое сделано учеными и инженерами США, Японии, ФРГ, Англии, Канады, России, Украины и других стран, где существуют крупнейшие исследовательские центры, оснащенные современным оборудованием.
Построенные в 1970-1980 гг. крупнейшие мосты (пролетами от 194 до 720 м) в Киеве, Риге, Днепропетровске, Череповце, через р. Амударья вывели страны СНГ на передовые рубежи современного мостостроения. Эти мосты проектировались на современной научной основе, с использованием теоретических и экспериментальных исследований на всех стадиях создания сооружений.
Общие сведения из аэродинамики мостов
Даже при равномерном обтекании пролетного строения потоком воздуха могут возникнуть вынужденные колебания. Основная причина этого явления заключается в образовании вихревого следа, завихрений при обтекании воздухом какого-либо препятствия. По имени французского ученого Т. Кармана это явление называется «дорожка Кармана» (рис. 16.1, а).
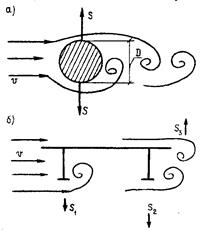
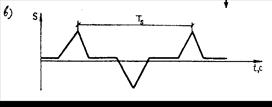
Рис. 16.1. Возникновение дорожки Кармана (а, б)
и график силы S (в) от вихрей Кармана
Вихри Кармана формируются поочередно за обтекаемым телом с разных сторон по ходу потока, вызывая вибрацию пролетного строения в направлении, перпендикулярном потоку. Другими словами, на пролетное строение действует сила S, перпендикулярная его оси и периодически изменяющаяся во времени (рис. 16.1). Период силы S(Ts), а точнее частота срыва вихрей Кармана зависит от многих факторов, важнейшими из них являются (см. рис. 16.1):
- скорость потока v и его плотность r (r = 1,225 кг/м3);
- размер сооружения D;
- форма конструкции (безразмерный параметр, учитывающий форму при обтекании жидкостью или газом, известен под названием «число Струхаля» 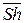 = QD / v).
= QD / v).
Тогда в общем виде можно записать [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]:
S = f(v, p, D,  ) sin Qt, (16.1)
) sin Qt, (16.1)
где Q - круговая частота образования вихрей Кармана.
В случае совпадения частоты Q действия силы S с собственными частотами wв, wг, wк пролетного строения мост начнет испытывать колебания либо в вертикальной, либо в горизонтальной плоскостях. Могут возникнуть и крутильные колебания за счет несимметричного приложения возмущающих сил S1, S2 и несовпадения их частот Q1, Q2 (см. рис. 16.1, б). На практике колебания пролетного строения происходят еще сложнее, так как ветер может действовать под углом к конструкции (и в вертикальной и в горизонтальной плоскостях) и отдельными порывами. Вследствие этого причинами аэроупругих колебаний гибких тел в ветровом потоке могут быть различные силы, которые вызывают многообразные виды аэродинамической неустойчивости.
Дадим краткое описание наиболее опасных аэроупругих явлений[Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с., Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.] (рис. 16.2).
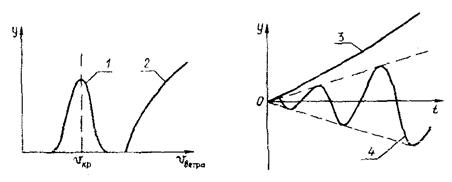
Рис. 16.2. Графики некоторых аэроупругих явлений:1 - ветровой резонанс;
2 - галопирование; 3 - дивергенция; 4 - флаттер
1) Флаттер (изгибно-крутильный или классический) - связанные изгибно-крутильные быстро нарастающие во времени самовозбуждающиеся колебания. Причина в несовпадении точки приложения аэродинамических сил с центром изгиба поперечного сечения балки жесткости моста; срывной флаттер возникает за счет срыва воздушных вихрей.
2) Бафтинг - наблюдается у элементов конструкции, находящихся в турбулентном потоке или в следе за другими элементами из-за интерференции аэродинамических сил.
3) Ветровой резонанс- нарастание амплитуд автоколебаний поперек потока воздуха, наблюдаемое при совпадении частоты Q срыва вихрей Кармана с одной из собственных частот wi (см. рис. 16.1).
4) Галопирование -раскачивание, которому подвержены плохо обтекаемые гибкие элементы с аэродинамически неустойчивыми поперечными сечениями (квадратными, прямоугольными). Подобные явления чаще всего возникают у канатов в случае их покрытия льдом. Галопирование опаснее резонанса, так как оно нарастает с увеличением скорости потока даже выше критической, а резонанс возникает только при критической скорости ветра.
5) Параметрический резонанс- заключается в «перекачке энергии» вертикальных колебаний в горизонтальные и наоборот. Наблюдается при кратности частот wв и wг.
6) Дивергенция- потеря устойчивости от крутильных колебаний.
Методика проверки аэродинамической устойчивости висячих и вантовых мостов
Методика проверки аэродинамической устойчивости мостовзаключается в определении критической скорости ветра для конкретного пролетного строения vкр. Это такая скорость ветра, при которой на данном пролетном строении возникает одно из аэроупругих явлений (флаттер, бафтинг, галопирование, дивергенция или ветровой резонанс). Проверка аэродинамической устойчивости состоит из условия [СНиП 2.05.03-84. Мосты и трубы / Госстрой СССР. М., 1985. 200 с., Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с.]:
vкр>> vр (16.2)
(минимальное превышение vкр СНиПом определяется в 1,5 раза: vкр > 1,5 vр (п. 2.24), где vр - расчетная скорость ветра, т.е. максимально возможная, для заданного района строительства моста. Обычно величина vрнаходится в пределах 25...35 м/с.
Определение критической скорости для висячих или вантовых мостов - весьма сложная задача, так как vкр зависит от многих факторов: от формы и размеров конструкции, ее массы, динамических характеристик балки жесткости (wi), климатических условий и т.д. Влияние отдельных факторов в настоящее время оценивается только экспериментальным путем или на основе приближенного анализа.
Поэтому в курсовом и дипломном проектировании для вычисления v рекомендуется воспользоваться упрощенными методами: либо материалами исследований В. Курлянда [Курлянд В.Г. Аэродинамические и аэроупругие характеристики пролетных строений мостов: Автореф. дис. ... канд. техн. наук. М., 1981. 20 с.], выполненных в аэродинамической трубе на различных моделях мостов, либо по формулам и графикам, представленным в [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]. Согласно методике [ Курлянд В.Г. Аэродинамические и аэроупругие характеристики пролетных строений мостов: Автореф. дис. ... канд. техн. наук. М., 1981. 20 с.], величина v равна:
vкр = vкр, м wк В, (16.3)
где vкр, м - приведенная критическая скорость, полученная при испытаниях моделей (табл. 16.1 и 16.2); wк - частота крутильных свободных колебаний, 1/с; В - ширина моста, м.
Величины vкр, м для различных типов поперечных сечений балок жесткости (рис. 16.3) приведены в табл. 16.1 . Для сечений улучшенной обтекаемости (рис. 16.4) vкр, м зависит не только от формы сечения, но и от параметра y =wк/wв и может быть найдена по интерполяции из табл. 16.2.
Таблица 16.1
Значения vкр, м для пролетных строений (рис. 16.3)
| Тип сечения | А1 | А2 | A3 | А4 | A5 | A6 | A7 | A8 | B1 | B2 | В3 | B4 | B5 |
| Vкр,м | 4,0...6,0 | 4,5...5,5 | 4,5...6,0 | 6,5...7,5 | 8,0 | 7,5 | 6,5 | 5,0 | 5,0 | 6,0 | 8,0 | 7,0 | 6,0 |
Таблица 16.2
Значения vкр, м для конструкций улучшенной обтекаемости (рис. 16.4)
| Тип сечения | С1 | С2 | C3 | C4 | C5 |
| y = 1,2 | 9,0 | 13,0 | 12,0 | 12,5 | 15,0 |
| y = 2,5 | 16,0 | 23,0 | 21,0 | 21,0 | 24,0 |
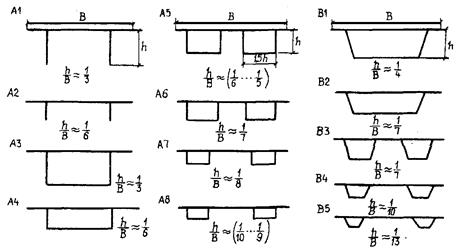
Рис. 16.3. Поперечные сечения балок жесткости
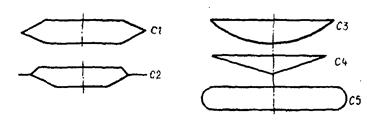
Рис. 16.4. Поперечные сечения балок жесткости улучшенной обтекаемости
Основные сложности состоят в определении частот крутильных колебаний:
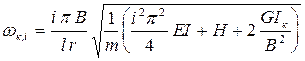 , (16.4)
, (16.4)
где r - радиус инерции сечения балки с проезжей частью относительно продольной оси; GIк - крутильная жесткость поперечного сечения балки.
Определение величин r, GIк весьма громоздко, поэтому в курсовом проекте допускается принять приблизительную зависимость wк,i » (1...4)wв,i, где минимальные значения коэффициента в скобках назначаются для поперечных сечений балок жесткости с плохой обтекаемостью (А1-А2), а максимальные - с хорошей обтекаемостью (С1-C5). Остальным типам балки жесткости (А3-А8, В1-В5) можно назначить средние значения этого коэффициента.
В дипломном проекте рекомендуется определить величину vкр по материалам [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]. Рассмотрим пример Такомского моста, имевшего в 1940 г. поперечное сечение, крайне неудачное с точки зрения аэродинамической устойчивости (рис. 16.5, а). Параметры пролетного строения: l = 855 м; В = 12 м (В/l =1/72); h =2,5 м (h/l = 1/350); m = 8,25 т/м; wв,2 = 0,83 1/с; wк,2 =1,73 1/с. По графикам и формулам [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.] величина vкр = 15 м/с. Несомненно, значение чрезвычайно низкое, такой ветер не является редким явлением в любом районе. Катастрофа и произошла при v= 19 м/с.
Новый Такомский мост выполнен следующим образом: вместо балки принята ферма жесткости hф =10 м (h/l =1/86); Вф = 18 м (1/50l) (рис. 16.5, б). Для данного пролетного строения vкр = 60 м/с [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.], что является вполне допустимым с точки зрения аэродинамической устойчивости.
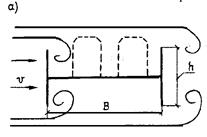
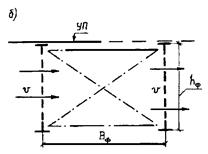
Рис. 16.5. Схемы поперечных сечений Такомского моста
Кроме того, можно рекомендовать в курсовом и дипломном проектах проверить аэродинамическую устойчивость по приближенным критериям. Согласно критериям Д. Штейнмана [Вантовые мосты / А.А. Петропавловский, Е.И. Крыльцов, Н.Н. Богданов и др.; Под ред. А.А. Петропавловского. М.: Транспорт, 1985. 224 с.], висячий мост аэродинамически устойчив, если
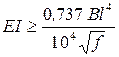 , (16.5)
, (16.5)
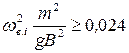 , (16.6)
, (16.6)
а по критерию P. Аммана, если
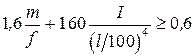 . (16.7)
. (16.7)
В случае невыполнения условий (16.2), (16.5), (16.7) следует откорректировать параметры моста.
Проверка аэродинамической устойчивости висячих
и вантовых мостов в горизонтальной плоскости
Заканчивая расчет моста на действие ветровой нагрузки, необходимо проверить его работу в горизонтальной плоскости,рассмотрев статическое воздействие ветра. Величина интенсивности ветровой нагрузки на боковую поверхность моста w определяется по СНиП и материалам [Казакевич M.И. Аэродинамика мостов. М.: Транспорт, 1987. 240 с.]. После этого следует проверить прочность балки на изгиб в горизонтальной плоскости (sб < Rу) и на максимальный прогиб [Качурин В. К., Брагин А.В., Ерунов Б. Г. Проектирование висячих и вантовых мостов. М.: Транспорт, 1971. 280 с.]:
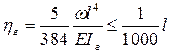 . (16.8)
. (16.8)
При невыполнении условия (16.8) устанавливаются ветровые оттяжки (см. рис. 16.6, а).
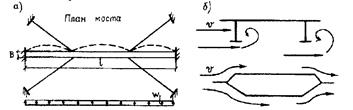
Рис. 16.6. Способы повышения горизонтальной жесткости
Меры по повышению аэродинамической устойчивости висячих и вантовых мостов
Меры по повышению аэродинамической устойчивости висячих и вантовых мостовнаправлены на уменьшение различных видов колебаний: вертикальных, горизонтальных, крутильных, изгибно-крутильных. Выделим наиболее эффективные меры, сгруппировав их по виду колебаний, возникновению которых они препятствуют в большей степени.
1. Вертикальные колебания:
- повышение жесткости пролетного строения ЕI,
- увеличение постоянной нагрузки р.
2. Горизонтальные колебания:
- увеличение ширины моста В,
- постановка ветровых горизонтальных предварительно напряженных оттяжек (рис. 16.6, а).
3. Крутильные колебания:
- применение жестких пространственных конструкций, в первую очередь, коробчатых.
4. Изгибно-крутильные колебания:
- применение ферм жесткости (дробление воздушного потока);
- применение балок жесткости улучшенной обтекаемости (рис. 16.6, б) или устройство обтекателей из легких металлов для обычных балок (рис. 16.7);
- применение сквозной проезжей части из системы вертикальных ребер вместо плиты (для автодорожных мостов).
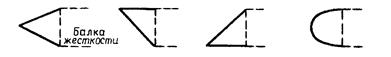
Рис. 16.7. Модели обтекателей для балок жесткости
| <== предыдущая лекция | | | следующая лекция ==> |
| Теоретические основы расчета вантовых мостов | | | Инженерное творчество как часть современной социотехнической реальности |
Дата добавления: 2021-06-28; просмотров: 893;











