Относительный покой жидкости

Из уравнения гидростатики, определяющего равновесие покоящейся жидкости , запишем:

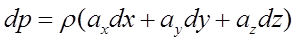. (3.1)

Для поверхности равного давления (dp=0) имеем

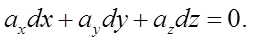(3.2)

При вращении сосуда с жидкостью с постоянной скоростью вокруг вертикальной оси на каждую частицу жидкости действуют массовые силы–сила тяжести и центробежная сила инерции.

Проекции ускорения массовых сил а_х, а_у, a_z на оси координат в данном случае будут (рис. 3.1):

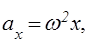
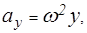
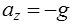
С учетом этого выражение (3.2) примет вид

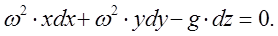(3.3)

Интегрирование последнего выражения дает уравнение параболоида вращения:

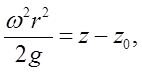(3.4)

где 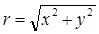; х, у, z - текущие координаты точек на свободной поверхности жидкости; z₀ - координата пересечения параболоида с осью вращения; w - угловая скорость вращения; ρ - плотность жидкости.

Закон распределения давления в жидкости при относительном покое имеет вид

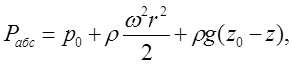(3.5)

где Р_абс - абсолютное давление в любой точке жидкости с текущими координатами r и z (рис. 3.1).

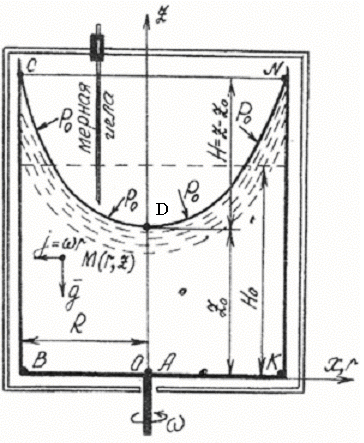
Рис. 3.1. Схема установки для изучения относительного покоя жидкости во вращающемся относительно вертикальной оси цилиндре

Например: если точка А находится на дне резервуара, совпадая с началом координат, тогда r = 0, z = 0, по уравнению (3.5) имеем

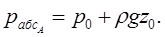(3.6)

Если точка В находится на дне резервуара у его боковой стенки (рис. 3.1), имеем r = R, z = 0, тогда по уравнению (3.5)

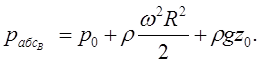(3.7)

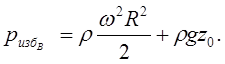(3.7)*

Изменение давления по вертикали такое же, как и в неподвижном сосуде.