Определение коэффициентов местных сопротивлений

При движении жидкости по трубопроводу часть энергии (напора) теряется на преодоление гидравлических сопротивлений, вызванных установкой трубопроводной арматуры (внезапное сужение, внезапное расширение, тройник, крестовина, колено, кран, вентиль, задвижка, диафрагма и т.д.).Эти гидравлические сопротивления называются местными, а потери энергии на них местными потерями.

Особенностью местных сопротивлений являетсяналичие при турбулентном режиме вихревыхзон (рис. 7.1) и деформации эпюры скоростей.

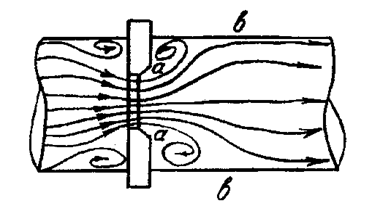
Рис.7.1. Кинематическая структура потока в зоне местного сопротивления диафрагмы

Транзитный поток отделен от вихревой зоны осредненной во времени и пространстве поверхностью раздела ab. Транзитная струя в области вихревой зоны неустойчива. Поэтому поверхность раздела аb является зоной интенсивного вихреобразования и перехода механической энергии в тепловую. В виду большой сложности явлений, происходящих вжидкости, протекающей через местное сопротивление, только в отдельных случаях коэффициент x может быть найден теоретически. В преобладающем большинстве случаев x определяется опытным путем. Исследования, проведенные учеными, показали, что зависимость коэффициента x от Re наблюдается при ламинарном режиме движения жидкости. В турбулентном потоке влияние числа Re на коэффициент x весьма незначительно. При практических расчетах в области турбулентного режима движения этот коэффициент зависит только от вида и конструктивного выполнения местного сопротивления.

При экспериментальных исследованиях потери энергии (напора) определяются из уравнения Бернулли при условии h_м ¹ 0, h_l = 0.

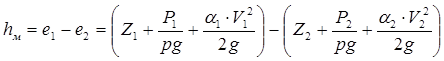, (7.1)

где 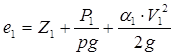– полная удельная энергия потока перед местным сопротивлением;

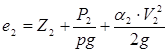– полная удельная энергия потока после местного сопротивления.

Величина коэффициента местного сопротивления определяется по формуле

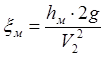. (7.2)