Метод прямоугольников

Заменим подынтегральную функцию f(x) в пределах элементарного отрезка [x_i;x_i+1] интерполяционным многочленом нулевой степени (рис.1.4.2-1), то есть постоянной величиной, равной либо f(x_i), либо f(x_i+1).

Рис. 1.4.2-1

Значение элементарного интеграла равно площади прямоугольника, в первом случае
I = h∙f(x_i), а во втором I = h∙f(x_i+1), где h = x_i+1 - x_i. Для определения значения интеграла на отрезке [a;b] найдем суммы элементарных интегралов, взяв в первом случае в качестве
f(x)– значение подынтегральной функции в левом конце i-го отрезка, а во втором – в правом конце отрезка:

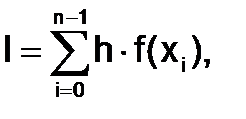(1.4.2-1)
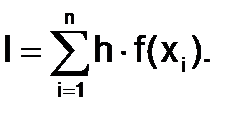(1.4.2-2)

Формула (1.4.2-1) называется формулой левых прямоугольников, а формула
(1.4.-2.2) – формулой правых прямоугольников.

Для вычисления определенного интеграла может быть использована и формула средних прямоугольников (1.4.2-3), в которой на элементарном отрезке интегрирования функция f(x)тоже заменяется интерполяционным многочленом нулевой степени, но равным значению функции в середине отрезка:

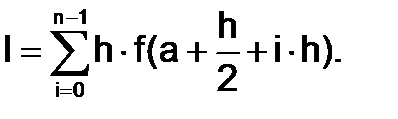(1.4.2-3)

Схема алгоритма метода средних прямоугольников приведена на рис. 1.4.2-2.

Рис. 1.4.2-2. Схема алгоритма интегрирования по методу средних прямоугольников с

использованием правила Рунге

Формула трапеций

Разобьем интервал интегрирования [a;b] на n равных отрезков (рис. 1.4.3-1) и восстановим из полученных точек a, х₁, x₂, …, bперпендикуляры до пересечения с графиком функции. Соединив последовательно точки пересечения, представим площадь полученной криволинейной трапеции как сумму прямолинейных трапеций, площади которых легко подсчитать. Заменив подынтегральную функцию f(x)в пределах элементарного отрезка [x_i;x_i+1] интерполяционным многочленом первой степени, получим следующие формулы для элементарных площадей:

Рис. 1.4.3-1

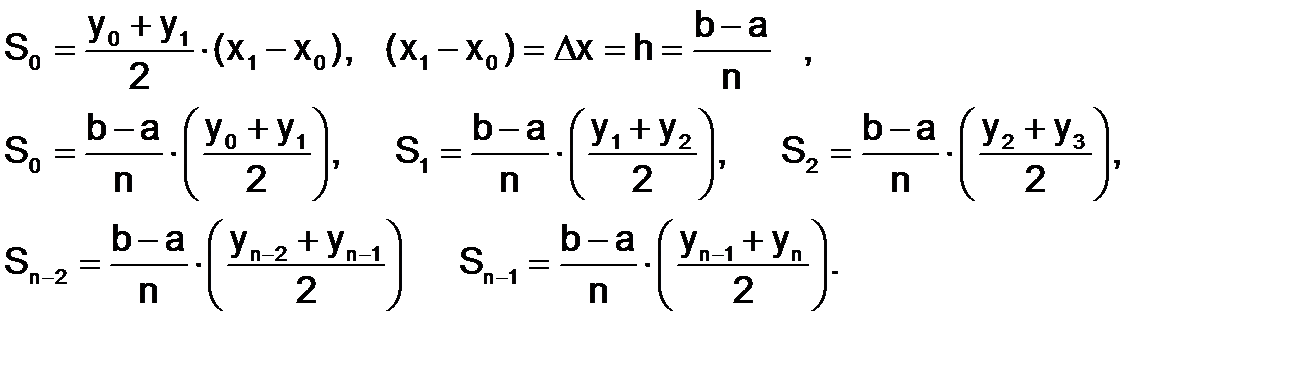
Тогда общая площадь равна: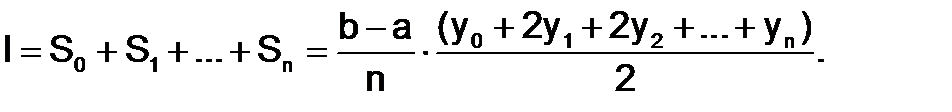

Отсюда получаем формулу трапеций:

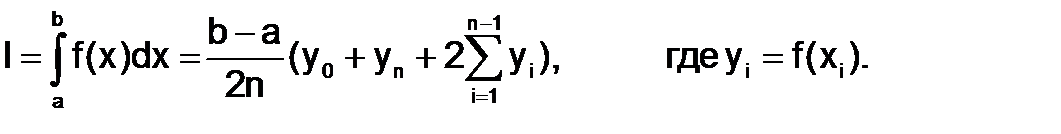(1.4.3-1)

Схема алгоритма метода трапеций приведена на рис. 1.4.3-2.

Рис. 1.4.3-2. Схема алгоритма интегрирования по методу трапеции с использованием

правила Рунге

Формула Симпсона

Для получения формулы Симпсона применяется квадратичный интерполирующий полином, следовательно, за элементарный интервал интегрирования принимается отрезок [x_i;x_i+2]. Поэтому разобьем интервал интегрирования [a;b] наn отрезков, где n=2m – четное число (рис. 1.4.4-1).

Рис. 1.4.4-1

Для получения интерполирующей функции на интервале [x_i;x_i+2] воспользуемся первой интерполяционной формулой Ньютона, используя в качестве узлов интерполяции точки x_i, х_i+1 и x_i+2.

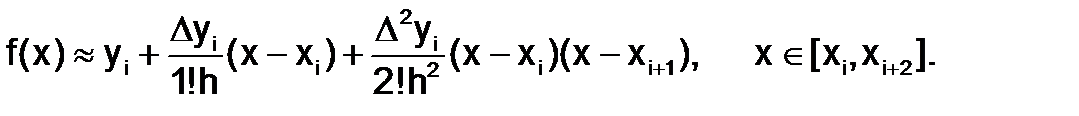(1.4.4-1)

В пределах отрезка [x_i;x_i+2], на котором подынтегральная функция аппроксимирована многочленом (1.4.4-1), получим приближенную формулу Симпсона:

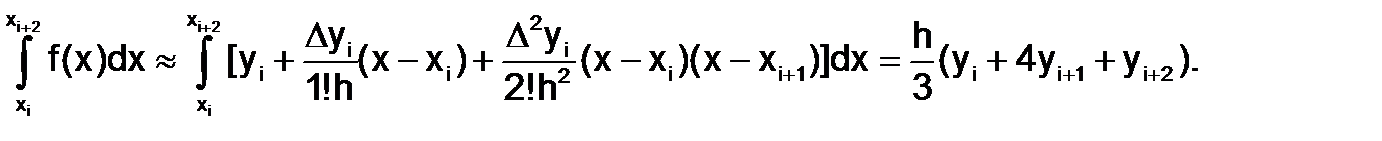(1.4.4-2)

Для отрезка [x₀;x₂]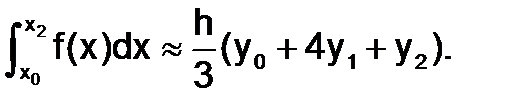

Для отрезка [x₂;x₄]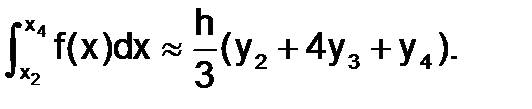

Тогда для всего интервала интегрирования [a;b] формула Симпсона выглядит следующим образом:

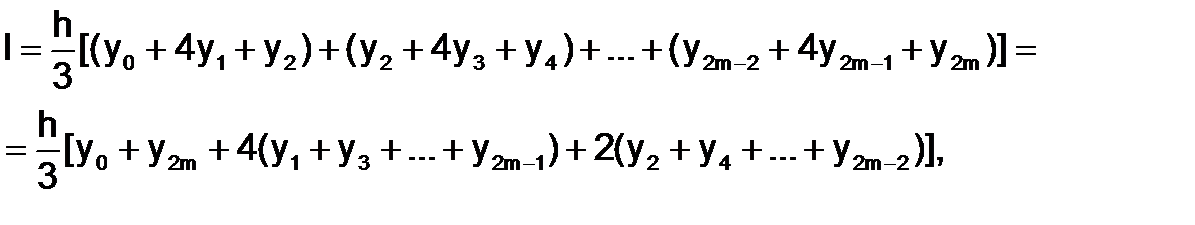
или

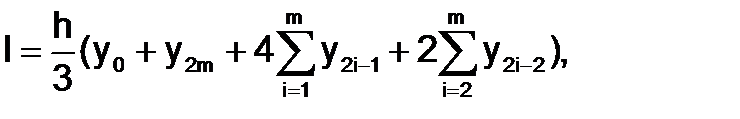(1.4.4-3)

при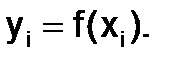

Схема алгоритма метода Симпсона приведена на рис. 1.4.4-2.

Рис. 1.4.4-2. Схема алгоритма интегрирования по методу Симпсона с использованием

правила Рунге