Касательная плоскость и нормаль к поверхности

Пусть функция 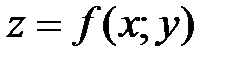дифференцируема в некоторой области D, точка .

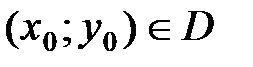x

y

z

x₀

y₀

M₀

O

b

a

Рисунок 1

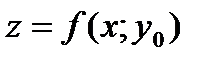
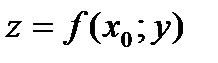
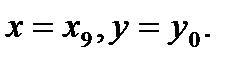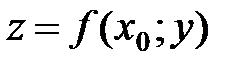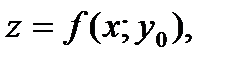Пересечем поверхность S, изображающую функцию. плоскостями Плоскости пресекают поверхность S по линиям и к каждой из которых в силу дифференцируемости функции в точке 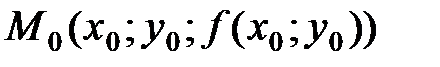можно провести касательные l₁ и l₂ (рис. 1)

Прямые l₁ и l₂ определяют плоскость 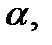которая называется касательной плоскостью к поверхности S в точке М.

Получим уравнение этой плоскости. Так как плоскость проходит черед точку 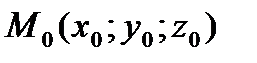будем искать ее уравнение в виде 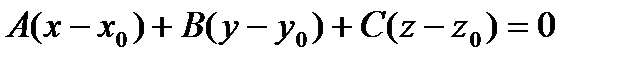Преобразуем данное уравнение к виду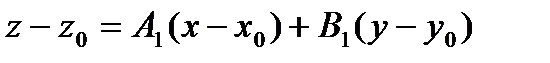

Найдем коэффициент А₁. Касательная l₂ лежит в плоскости 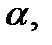, следовательно, координаты точек касательной удовлетворяют уравнению плоскости, поэтому имеет место система уравнений 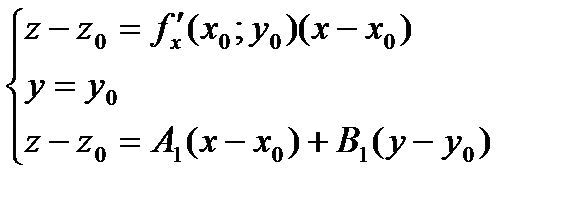. Решая систему. получим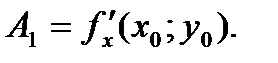

Аналогично получим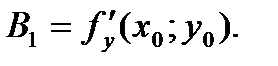

Подставим полученные выражения в уравнение касательной плоскости, тогда уравнение примет следующий вид:

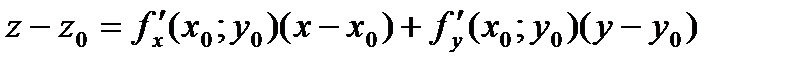(6).

Прямая, проходящая через точку 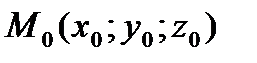и перпендикулярная касательной плоскости, построенной к этой поверхности, называется нормалью.

Уравнение нормали можно получить в каноническом виде, используя условие перпендикулярности прямой и плоскости (направляющий вектор прямой будет нормальным вектором для плоскости). Тогда уравнение нормали:

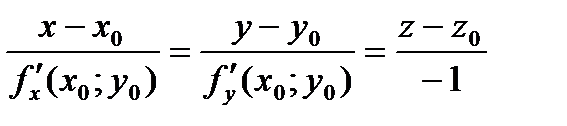(7)

Пример. Написать уравнение касательной плоскости и нормали к поверхности 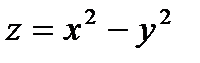в точке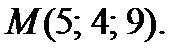

Решение. Найдем частные производные функции, их значения в точке М и воспользуемся уравнениями (6) и (7).

123 4

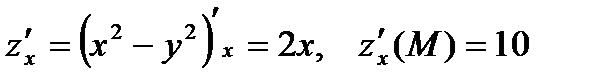
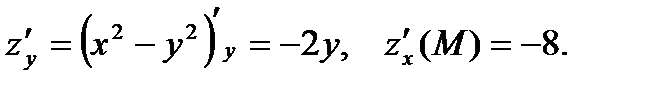
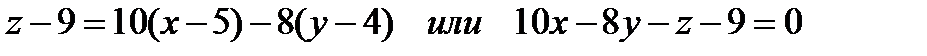
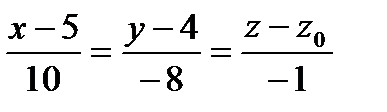
Дата добавления: 2021-02-19; просмотров: 334;