Теорема 1 (необходимое условие экстремума функции).
Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке 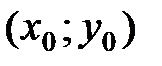 , то ее частные производные в этой точке равны нулю:
, то ее частные производные в этой точке равны нулю: 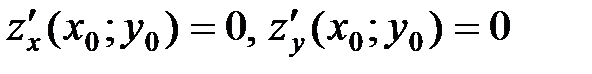 .
.
Критическими точками функции называются внутренние точки области определения, в которых частные производные первого порядка равны нулю или хотя бы одна из частных производных не существует.
Однако не любая критическая точка будет экстремумом функции. Примером, подтверждающим этот факт, может служить точка 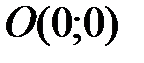 для функции
для функции 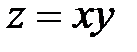 , которая является критической точкой, но не является экстремумом функции. Поэтому среди критических точек точки экстремума функции выявляют с помощьюдостаточного условия.
, которая является критической точкой, но не является экстремумом функции. Поэтому среди критических точек точки экстремума функции выявляют с помощьюдостаточного условия.
Теорема 2(достаточное условие экстремума функции).
Пусть в критической точке 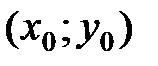 и некоторой ее окрестности функция
и некоторой ее окрестности функция 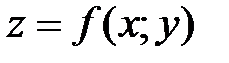 имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке
имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 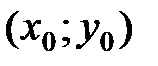 значения
значения 
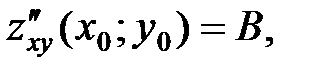
 . Обозначим
. Обозначим 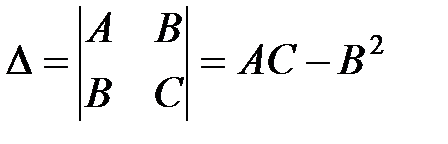 .
.
Тогда: 1) если 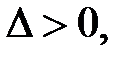 то функция в точке
то функция в точке  имеет экстремум: максимум, если А<0; минимум, если A>0; 2) если
имеет экстремум: максимум, если А<0; минимум, если A>0; 2) если 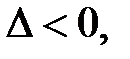 то функция в точке
то функция в точке 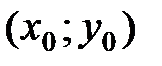 экстремума не имеет.
экстремума не имеет.
Замечание. В случае 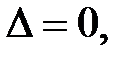 экстремум в точке
экстремум в точке 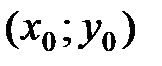 может быть, а может не быть. Необходимо дополнительное исследование.
может быть, а может не быть. Необходимо дополнительное исследование.
План нахождения экстремумов функции:
1) найти критические точки функции  ;
;
2) найти значение определителя  для каждой из критических точек;
для каждой из критических точек;
3) в соответствии с достаточным условием экстремума сделать вывод о наличии в ней экстремума и найти его значение.
Пример. Найти экстремум функции 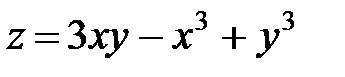 .
.
Решение. 1) 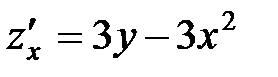 ;
; 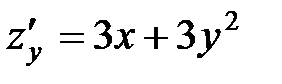 . Точки, в которых частные производные не существуют, отсутствуют.
. Точки, в которых частные производные не существуют, отсутствуют.
Найдем точки, в которых они равны нулю, решая систему уравнений: 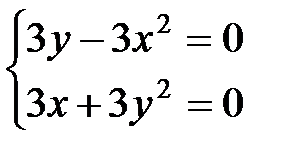 .
.
Получаем следующие точки: 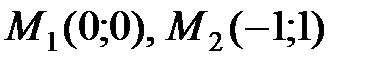 .
.
2) Находим частные производные второго порядка: 
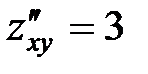 ,
, 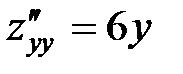 .
.
В точке 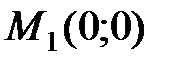 имеем: A=0, B=3, C=0, тогда
имеем: A=0, B=3, C=0, тогда 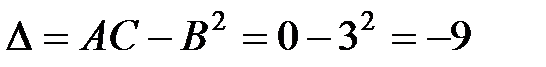 , т.е.
, т.е. 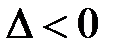 .
.
В точке 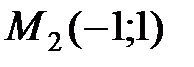 имеем: A=6, B=3, C=6, тогда
имеем: A=6, B=3, C=6, тогда  , т.е.
, т.е. 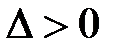 .
.
3) В точке  экстремума нет.
экстремума нет.
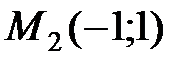 – точка минимума (A=6>0),
– точка минимума (A=6>0),  .
.
§ 4 Условный экстремум функции двух переменных
Иногда на практике возникает задача нахождения экстремума функции двух переменных x и y в случае, когда эти переменные не являются независимыми друг от друга. Соотношение между ними описывается уравнением  , которое называется уравнением связи. Такая задача нахождения экстремума функции
, которое называется уравнением связи. Такая задача нахождения экстремума функции 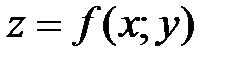 при условии, что x и y удовлетворяют уравнению связи
при условии, что x и y удовлетворяют уравнению связи  , и носит название задачи нахождения условного экстремума.
, и носит название задачи нахождения условного экстремума.
Опр. Точка 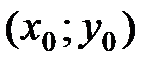 называется точкой условного максимума (условного минимума)функции
называется точкой условного максимума (условного минимума)функции 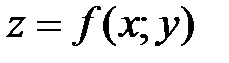 , при условии
, при условии  , если существует такая d-окрестность точки
, если существует такая d-окрестность точки 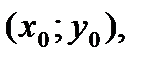 что для каждой точки
что для каждой точки 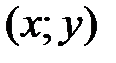 , отличной от точки
, отличной от точки 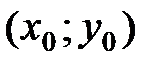 , координаты которой удовлетворяют уравнению
, координаты которой удовлетворяют уравнению  , из этой окрестности выполняется неравенство
, из этой окрестности выполняется неравенство 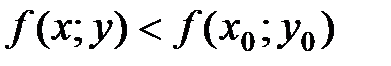 (
( 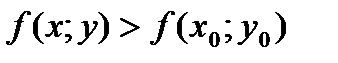 ).
).
Существует два способа решения этой задачи.
Первый способ.
Если уравнение  разрешимо относительно одной из переменных x или y, тогда из уравнения связи выражают одну переменную через другую и подставляют найденное выражение в функцию
разрешимо относительно одной из переменных x или y, тогда из уравнения связи выражают одну переменную через другую и подставляют найденное выражение в функцию 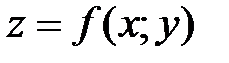 . В результате получают функцию z одной переменной x или y и исследуют ее на экстремум.
. В результате получают функцию z одной переменной x или y и исследуют ее на экстремум.
Второй способ (является универсальным)
Составляют так называемую функцию Лагранжа: 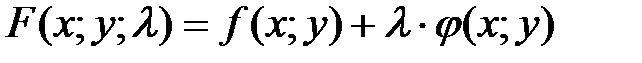 , где l – вспомогательный множитель.
, где l – вспомогательный множитель.
Верна следующая теорема.
Теорема. Если точка 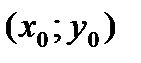 является точкой условного экстремума функции
является точкой условного экстремума функции 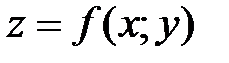 при условии
при условии 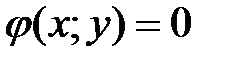 , то существует единственное значение l0, такое, что точка
, то существует единственное значение l0, такое, что точка 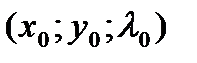 является точкой экстремума функции
является точкой экстремума функции 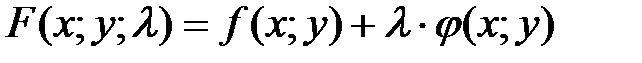 .
.
Для отыскания условных экстремумов данным способом сначала находят критические точки функции Лагранжа, решая систему уравнений:
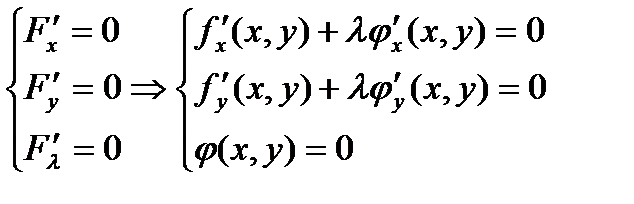 .
.
Определить вид экстремума в найденных критических точках можно следующим способом. Для каждой из критических точек составляем определитель:
 , где
, где 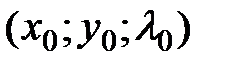 – координаты критической точки. Если
– координаты критической точки. Если 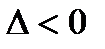 , то в точке
, то в точке 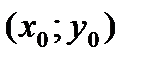 условный максимум. Если
условный максимум. Если  , то в точке
, то в точке  условный минимум.
условный минимум.
Замечание. Это один из способов определения вида экстремума. Существуют и другие, познакомиться с которыми можно в соответствующей литературе.
Пример. Найти условный экстремум функции  , если
, если 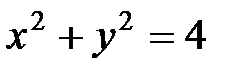 .
.
Уравнение связи  не может быть разрешено однозначно относительно переменной x или y. Преобразуем его:
не может быть разрешено однозначно относительно переменной x или y. Преобразуем его: 
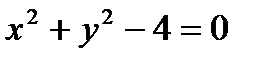 .
.
Составим функцию Лагранжа: 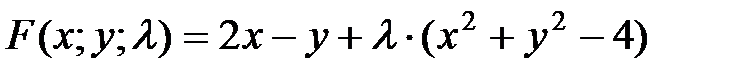 .
.
Найдем частные производные первого порядка функции 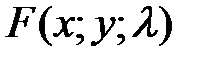 :
: 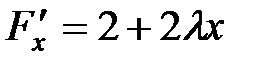 ,
,  ,
,  .
.
Решая систему уравнений 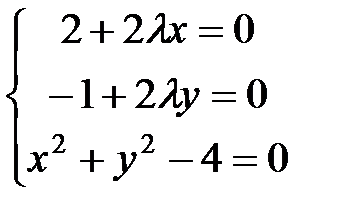 , находим критические точки
, находим критические точки 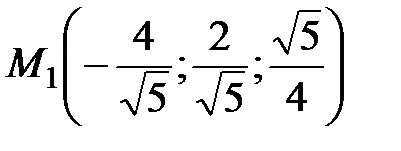 ,
, 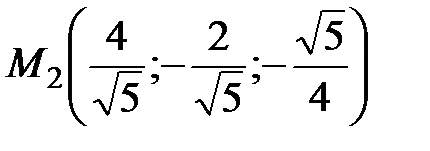 .
.
Определим вид экстремумов.
Сначала находим частные производные первого порядка функции 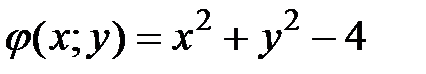 и частные производные второго порядка функции Лагранжа
и частные производные второго порядка функции Лагранжа 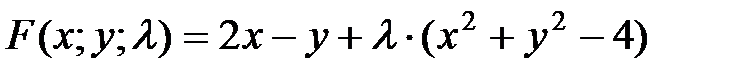 :
:
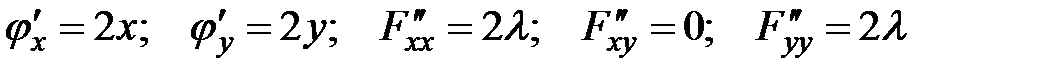 .
.
Тогда
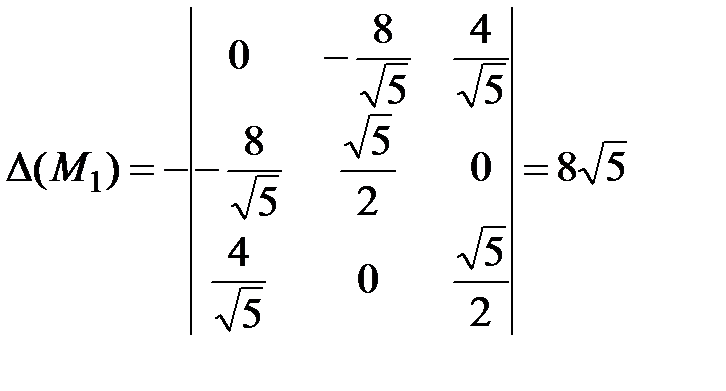 >0;
>0; 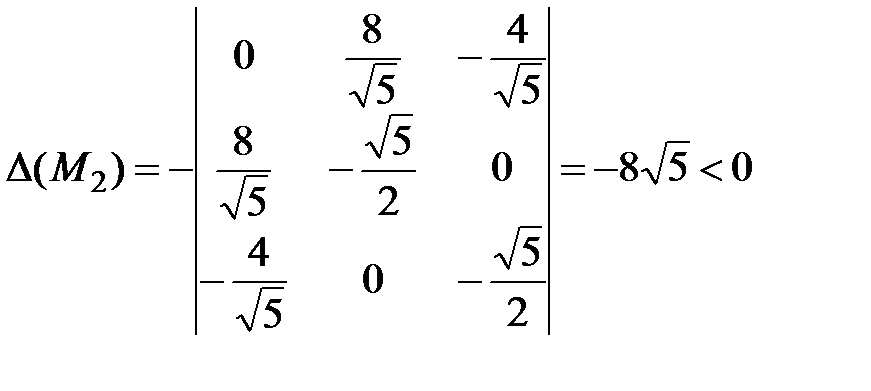 .
.
Значит,  – условный минимум,
– условный минимум, 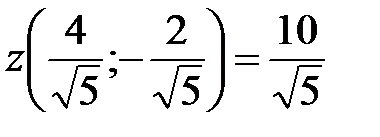 – условный максимум.
– условный максимум.
Дата добавления: 2021-02-19; просмотров: 536;











