Производная по направлению. Градиент функции
Пусть функция 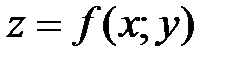 определена в некоторой окрестности точки
определена в некоторой окрестности точки 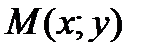 , l – некоторое направление, задаваемое единичным вектором
, l – некоторое направление, задаваемое единичным вектором 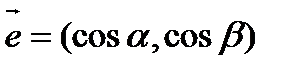 , где
, где 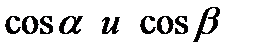 - направляющие косинусы вектора
- направляющие косинусы вектора 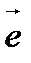 .
.
При перемещении в данном направлении l точки 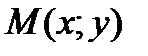 в точку
в точку 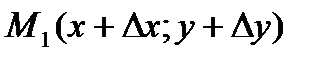 функция
функция 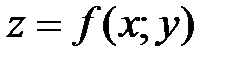 получит приращение
получит приращение 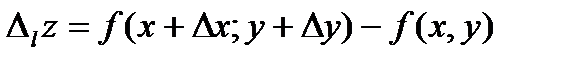 называемое приращением функции в направлении l .
называемое приращением функции в направлении l .
Опр. 1. Производной функции 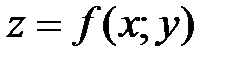 по направлению l называется предел отношения приращения функции в этом направлении к величине перемещения
по направлению l называется предел отношения приращения функции в этом направлении к величине перемещения 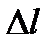 при стремлении последней к нулю, т.е.
при стремлении последней к нулю, т.е. 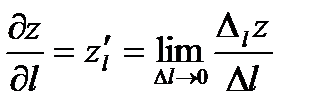 .
.
Производная 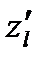 характеризует скорость изменения функции в направлении l. Рассмотренные ранее частные производные
характеризует скорость изменения функции в направлении l. Рассмотренные ранее частные производные 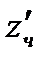 и
и 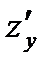 представляют собой производные по направлениям, параллельным соответственно осям Ох и Оу.
представляют собой производные по направлениям, параллельным соответственно осям Ох и Оу.
Примем без доказательства формулу для нахождения производно по направлению 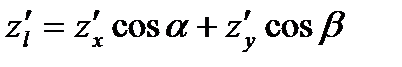 (5).
(5).
При вычислении производной по направлению полезны формулы
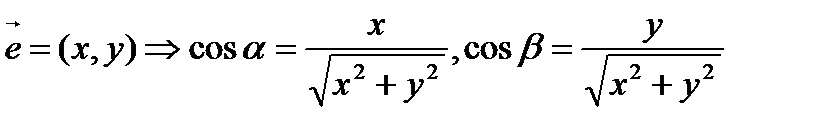 .
.
Пример1. Вычислить производную функции 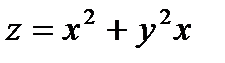 в точке
в точке 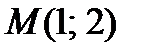 по направлению вектора
по направлению вектора 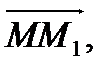 где
где 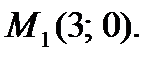
Решение. Найдем координаты вектора 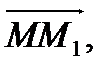 и его направляющие косинусы.
и его направляющие косинусы.
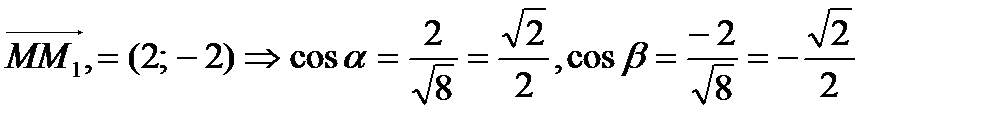
Находим частные производные функции их значения в точке М(1; 2)
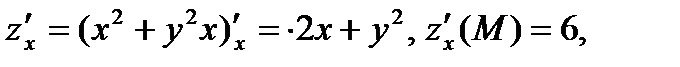
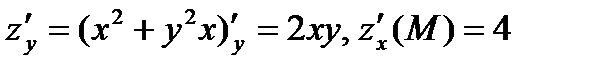
Применяем формулу (5) 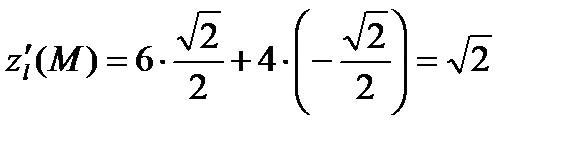
Опр. 2. Градиентом функции 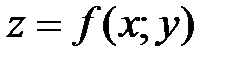 называется вектор с координатами
называется вектор с координатами 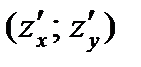 .
.
Обозначают вектор градиента одним из следующих способов 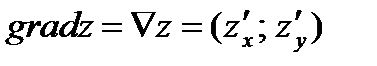 .
.
Рассмотрим физический смысл вектора градиента. Найдем скалярное произведение вектора 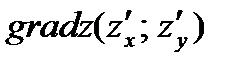 и единичного вектора
и единичного вектора 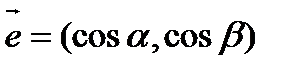 направления l .
направления l .
Получим: 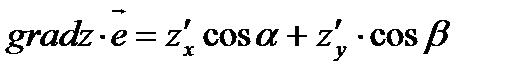 Сравнив полученное равенство с равенством (5) получим, что
Сравнив полученное равенство с равенством (5) получим, что 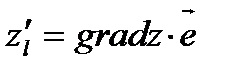 Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Таким образом, из всех направлений на плоскости в данной точке в направлении вектора градиента функция растет быстрее всего и имеет место формула
Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Таким образом, из всех направлений на плоскости в данной точке в направлении вектора градиента функция растет быстрее всего и имеет место формула
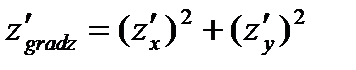
Пример 2. Найти градиент функции 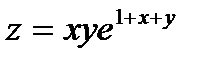 , его модуль и производную в направлении градиента в точке М(0; -1).
, его модуль и производную в направлении градиента в точке М(0; -1).
Решение. Находим частные производные функции и их значения в точке М.
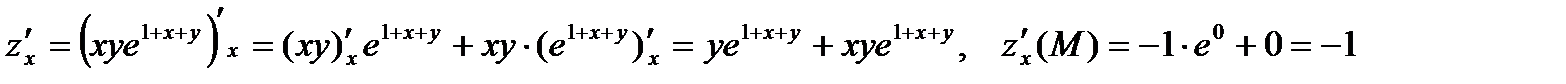
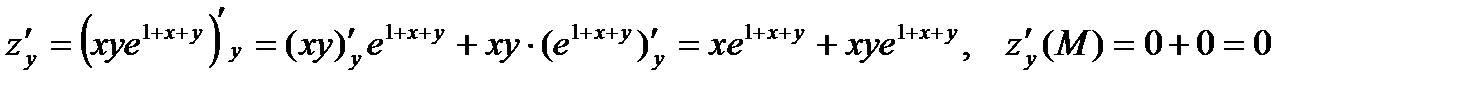
Тогда градиент функции равен 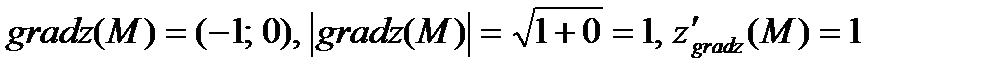 .
.
Дата добавления: 2021-02-19; просмотров: 544;











