Наибольшее и наименьшее значения функции

Пусть функция 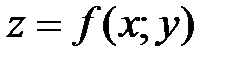определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках области D своего наибольшего и наименьшего значений (глобальные экстремумы). Эти значения достигаются функцией в точках, расположенных внутри области D. Или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области D.функции .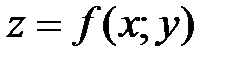

1) Найти критические точки функции, принадлежащие области D и вычислить значение функции в них.

2) Найти наибольшее и наименьшее значения функции на границах области D.

3) Сравнить все найденные значения и выбрать из них наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значение функции 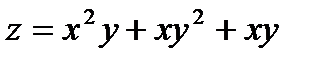в замкнутой области, ограниченной линиями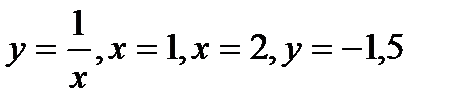

1) Изображаем область D.

2) Находим критические точки функции, решая систему

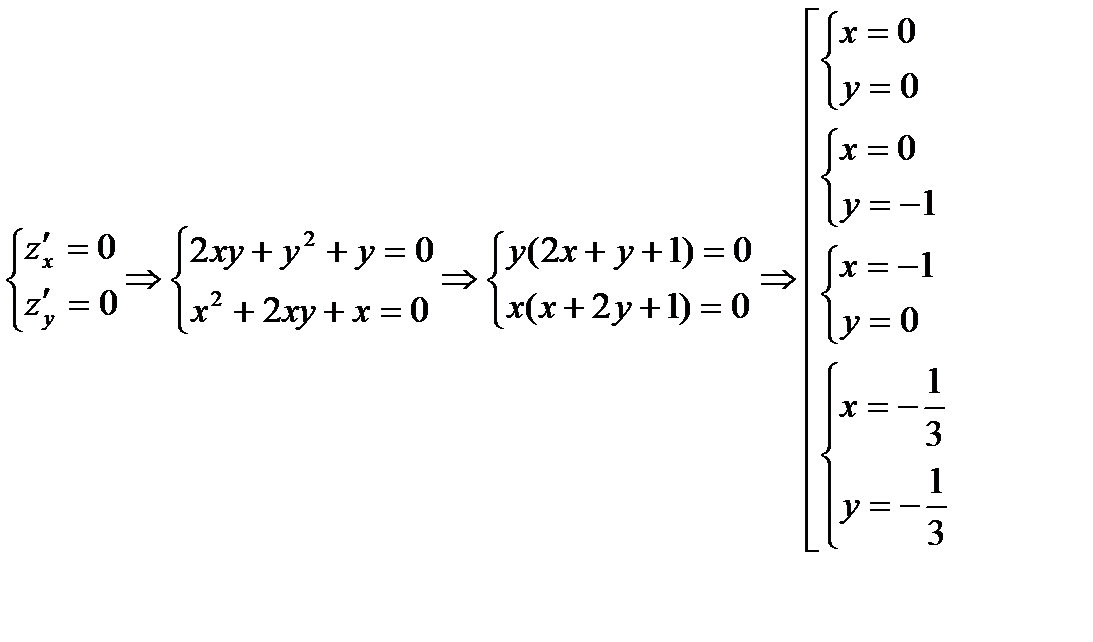
Из четырех полученных точек ни одна не принадлежит области D.

3) Исследуем функцию на границах области D.

АВ: 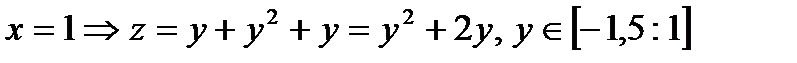Исследуем полученную функцию на наибольшее и наименьшее значения:

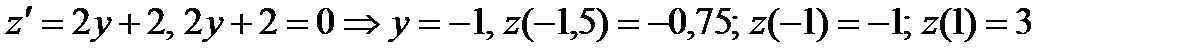
ВС: 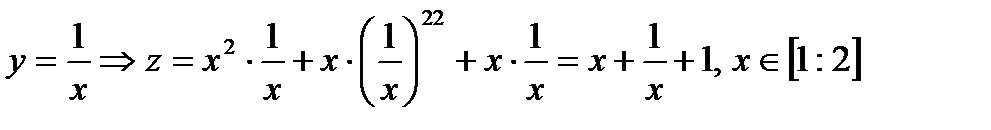Исследуем полученную функцию на наибольшее и наименьшее значения:

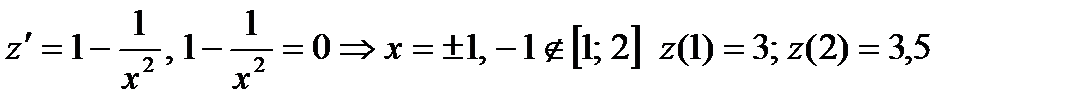
СЕ: 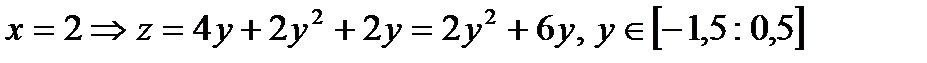Исследуем полученную функцию на наибольшее и наименьшее значения

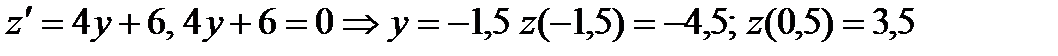
АЕ: 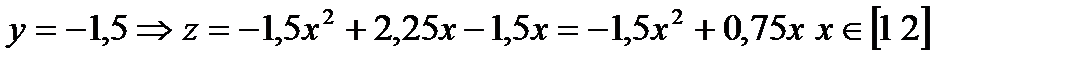Исследуем полученную функцию на наибольшее и наименьшее значения:

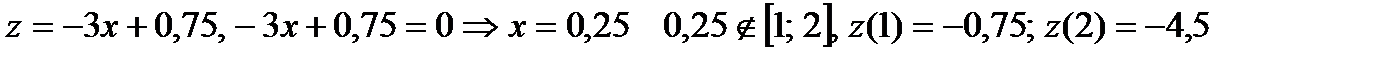
Сравнивая полученные результаты, получаем:

Наименьшее значение функции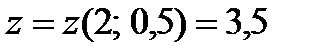

Наибольшее значение функции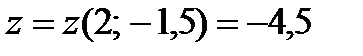

Ответ: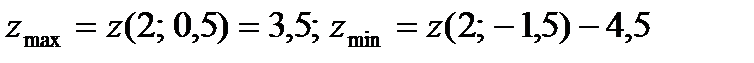

Литература:

1) Д. Письменный «Конспект лекций по высшей математике», глава 9, параграф 44, 46, п. 44.3, 44.5, параграф 45.

2) Н.Ш. Кремер «Высшая математика для экономистов», глава 15 п. 15.4, 15.5,15.6-15.8