Таким образом, в идеально твердом теле напряжение пропорционально не скорости развития деформации (как в жидком), а собственно деформации

Закон Гука также справедлив для деформации сдвига и для всестороннего (гидростатического) сжатия. В первом случае материал характеризуется модулем упругости при сдвиге G; во втором случае – объёмным модулем сжимаемости B. Обе эти величины не равны модулю Юнга.

Если известна пара констант: модуль E и коэффициент Пуассона μ , то можно определить две другие константы G= E/2(1+ μ) или B= E/2(1+ μ).

Решение уравнения (1) относительно динамической вязкости η дает:

η= 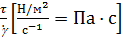(8)

Единица динамической вязкости η называется “паскаль • секунда” (Па·с). Также часто используется единица “миллипаскаль• секунда” (мПа·с).

1 Па • с = 1000 мПа • с.

Ранее употребляемая единица “сантипуаз” (сПз) для динамической вязкости) взаимозаменяема с мПа • с:

1 мПа • с = 1 сПз.

Кинематическая вязкость

При измерении вязкости ньютоновской жидкости в капиллярных вискозиметрах типа Уббелоде определяется ее кинематическая вязкость n. В данном случае образец жидкости течет через капилляр под действием силы тяжести.

Кинематическая вязкость nсвязана с динамической вязкостью ηсоотношением через плотность жидкости р:

v= 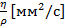(9)

Ранее в качестве единицы размерности кинематической вязкости ис­пользовали “Стокс” (Ст) или “сантиСтокс” (сСт); 1 Ст = 100 сСт, 1 мм²/с = 1 сСт.

Кривые течения и вязкости

Соотношение между напряжением сдвига и скоростью сдвига, характеризующее поведение жидкости при течении, графически изображается в виде кривой, на которой по оси ординат откладывают значения τ, а по оси абсцисс – 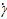. Такой график называют “кривой течения”.

Наиболее простой тип кривой течения приведен на рис. 3. При этом вязкость полагают постоянной и не зависящей от скорости сдвига.

Другой широко используемой диаграммой является зависимость вязкости от скорости или напряжения сдвига. Такая диаграмма называется “кривой вязкости”.

Кривая вязкости, представленная на рис. 4, соответствует кривой течения на рис. 3. Измерение вязкости прежде всего приводит к получению кривой течения. Затем эти результаты могут быть математически пересчитаны, чтобы получить соответствующую кривую вязкости.

Рис. 3. Кривая течения ньютоновской жидкости

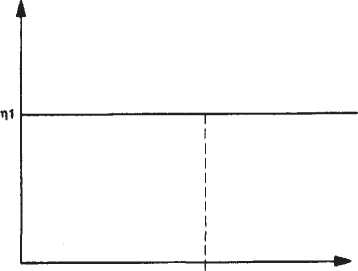Рис. 4. Кривая вязкости ньютоновской жидкости.

Измерения вязкости требуют соблюдения следующих условий:

1) Приложенный сдвиг должен приводить только к ламинарному, установившемуся во времени течению.

2) Приложенное напряжение сдвига должно быть передано от движущейся плоскости через граничный слой жидкости в ее объем т.е. не должно наблюдаться проскальзывания жидкости. В случае, если сцепления между движущейся плоскостью и жидкостью недостаточно для передачи напряжения сдвига и движущаяся плоскость скользит над неподвижным жидким образцом, результаты измерения будут бессмысленны.

3) Образцы должны быть «гомогенны». Смысл этого требования заключается в том, что испытуемый образец должен реагировать на сдвиг одинаково по всему объему. Если образцы являются дисперсиями или суспензиями, то все ингредиенты, капли или пузырьки должны быть очень малы по сравнению с толщиной слоя жидкости, подвергаемой сдвигу.

4) В процессе испытания в образце не должно происходить физических или химических изменений. Изменения испытуемого образца вследствие таких химических процессов, как затвердевание или разложение полимеров, или вследствие физических превращений, например взаимодействия между частицами и пластификаторами в ПВХ- пластизолях, оказывают вторичное влияние на вязкость. При обычной реометрии их следует избегать, за исключением тех случаев, когда именно эти влияния являются главной целью исследования.

5) Отсутствие упругости.Образцы жидкости должны быть чисто вязкими для того, чтобы к ним можно было применить простой закон вискрзиметрии. Суммарная энергия, переданная образцу, должна привести к истинному течению и в итоге – к полному превращению энергии сдвига в теплоту.

Хорошо известно, что в жидкостях могут наблюдаться следующие явления (см. рис. 5). Две различные жидкости, например вода и раствор каучука, не могут быть оптически различимы в состоянии покоя. Но при быстром перемешивании ротором они реагируют по-разному: вода отбрасывается центробежной силой, создаваемой вращением ротора, наружу и вверх по стенке сосуда, тогда как в другой, упругой жидкости, появляются нормальные напряжения, превышающие напряжения сдвига, которые заставляют жидкость подниматься по валу ротора.

Очень много таких образцов, как расплавы или растворы полимеров, а также очень много дисперсий под воздействием напряжения или скорости сдвига проявляют как вязкую, так и упругую реакцию, причем соотношение между первой реакцией и второй изменяется с изменением скорости сдвига. В то время как при очень низких скоростях сдвига все жидкости можно рассматривать как преимущественно вязкие и упругой компонентой при их течении можно пренебречь, то при высоких скоростях сдвига ситуация становится обратной.

Исследование вязкоупругого поведения в полном объеме преду­сматривает применение реометров, технически значительно усовер­шенствованных по сравнению с простыми вискозиметрами.

Свойство упругости в вязкоупругих жидкостях не может быть со­вершенно исключено, но можно найти такие условия испытания на вискозиметрах, особенно при достаточно низких скоростях сдвига, когда упругая реакция на сдвиг становится незначительной.

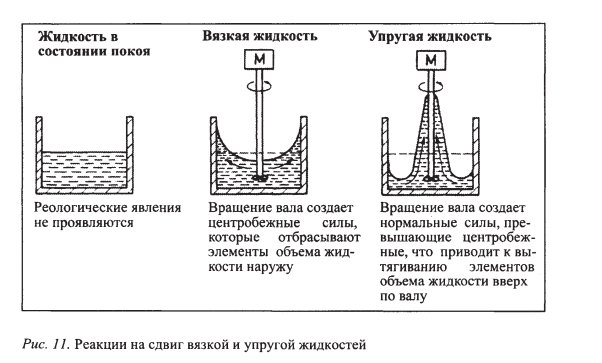
Рис.5. Реакции на сдвиг вязкой и упругой жидкости.