Понятие о жидких и твердых телах. Законы Ньютона и Гука. Кривые течения и вязкости.

В 1929 году профессор Юджин Бингам – физикохимик, работающий в колледже Лафайета в Пенсильвании, решил, что исследования деформации и потока вещества достаточно важны, чтобы иметь своё собственное название. По совету профессора античной литературы, он составил слово «реология» на основе греческого ρεω (рео), означающего поток. Однако дисциплина реология намного старше, чем слово. Первое формальное научное описание феномена реологии встречается в работе Исаака Ньютона «Начала математики», опубликованной в 1687 году, где он высказал мнение, что «сопротивление, возникающее от недостатка скользкости частиц какой-либо жидкости, при прочих равных условиях, пропорционально скорости, с которой частицы жидкости отделяются одна от другой». Сегодня мы могли бы сказать, что напряжение сдвига пропорционально скорости сдвига, и мы могли бы назвать коэффициент пропорциональности – вязкость жидкости.

Изучение упругости шло параллельно с изучением вязкости. Первая научная ссылка на упругость была сделана Робертом Гуком соперником Ньютона, состоявшим с ним в переписке, который опубликовал свою знаменитую анаграмму «CEIINOSSITTUV» в 1676 году, расшифрованную как «ut tensio sic vis» (каково удлинение, такова сила) в 1679 году. Закон Гука, как он стал называться, был обоснован экспериментальными наблюдениями, но лишь работа Юнга в начале девятнадцатого столетия показала, что этот закон может применяться к свойствам материала, а не просто к свойствам образца при растяжении. В современных терминах мы можем резюмировать открытия Юнга, сказав, что напряжение пропорционально нагрузке, и можем называть «коэффициент пропорциональности» «модулем материала».

Итак, реология – это наука о деформации и текучести веществ. Основной задачей реологии является изучение закономерностей поведения различных материалов под действием деформирующих усилий. При этом рассматриваются процессы, связанные с необратимыми остаточными деформациями и течением разнообразных вязких и пластичных материалов (неньютоновских жидкостей, дисперсных систем и др.), а также явления релаксации напряжений, упругого последействия и т.д.

Большинство материалов (твердых и жидких), используемых в промышленности, являются дисперсными системами. Изучение реологических свойств этих материалов входит в круг задач специального раздела общей реологии – реологии дисперсных систем, которая является также одним из разделов коллоидной химии – науки о дисперсных системах и поверхностных (межфазных) явлениях. Реологические параметры дисперсной системы позволяют судить о фундаментальном свойстве дисперсных частиц – о величине сил, действующих между частицами, о структуре системы. Справедливо и обратное: корректная оценка реологических параметров дисперсной системы возможна только на основе знания ее коллоидно-химических свойств. Можно смело утверждать, что переработка различных материалов таких как пищевые, строительные, фармацевтические и др. сопровождается сложнымифизико-химическими, биологическими и механическими процессами, изучение которых позволяет организовать эффективный и объективный контроль и управление технологическими циклами производства. Именно реологические исследования позволяют глубже познать физику явления, происходящего при обработке таких материалов.

Реологические свойства могут быть использованы в расчётах процессов, которые необходимо производить при создании новых конструкций машин и реконструкции существующих, а также для выбора наиболее рациональных режимов работы оборудования и оптимальных технологических схем производства, использовать в качестве контролируемых параметров при создании автоматизированных систем управления машинами, агрегатами, производственными участками, при автоматизированном контроле качества продукции. Реология позволяет управлять структурой и качеством продуктов путем внесения добавок, изменения режимов и способов механической и технологической обработки.

Введем некоторые понятия, которые будем в дальнейшем использовать.

Деформация – это изменение формы и (или) линейных размеров тела под действием внешних сил, при изменении влажности, температуры и др., при котором частицы или молекулы смещаются одна относительно другой без нарушения сплошности тела. Величина и характер деформации зависят от способа приложения внешних сил, свойств материала тела и его формы.

Деформацию делят на два вида: а) обратимую (упругую), которая исчезает после прекращения действия силы; б) пластическую (вязкую), которая не исчезает после снятия нагрузки. Кроме того, существует и другое деление. Например, различают деформацию сдвига (g), растяжения и сжатия (e).

Если деформации изменяются во времени t, то учитывают скорость деформации (градиент скорости) – 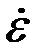[с^–1] при растяжении – сжатии и 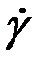[с^–1], при сдвиге:

;

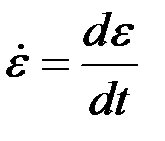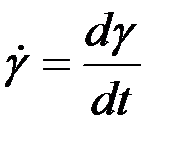
Напряжение – мера внутренних сил F [Н], возникающих в теле под влиянием внешних воздействий, отнесенная к единице площади А [м²],:

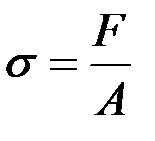, Па.

Если уменьшить площадь, то можно перейти к пределу, который даёт более строгое определение напряжения, поскольку оно относится к некоторой конкретной точке s= dF/ dS.

Полное описание напряжения как физического объекта требует идентификации двух векторов: вектора силы и вектора нормали к поверхности, по которой действует эта сила. Физические объекты, определяемые с помощью двух векторов, называют тензорами. Следовательно, напряжение – это тензорная величина. Различают сдвиговые или касательные напряжения (τ), направленные вдоль поверхности и нормальные напряжения (σ). Нормальные напряжения максимальны в таких направлениях, в которых касательные напряжения отсутствуют. Всегда существуют такие направления ориентации осей координат, в которых либо нормальные, либо касательные напряжения максимальны. Это обстоятельство интересно тем, что различные материалы по-разному сопротивляются действию растягивающих (нормальных) сил и сдвигу (тангенциальных, касательных сил). Например, трудно сжать воду или нефть, но сравнительно просто осуществить сдвиг одного слоя этих жидкостей относительно другого слоя внутри их объёма. Другой случай – тонкостенная труба под действием внутреннего давления разрушается вследствие приложения нормальных напряжений, в то время как касательные напряжения в этом отсутствуют.

Представляется очевидным, что только нормальные напряжения могут вызвать изменения объёма тела, в то время как действие касательных напряжений не приводит к изменению объёма тела, они могут только изменить форму тела. Изменение формы – это, в сущности, изменение расстояния между различными точками в объёме тела. Именно такой феномен называется деформацией. Деформацию как изменение расстояния между двумя точками можно описать, рассматривая перемещение в пространстве двух соседних точек. При этом важна не абсолютная величина изменения расстояния между точками, а относительное изменение расстояния. При одноосном растяжении любой образец претерпевает изменения и в поперечном направлении. Количественная связь между изменениями размеров деформируемого образца в продольном и поперечном направлениях определяется коэффициентом Пуассона m.

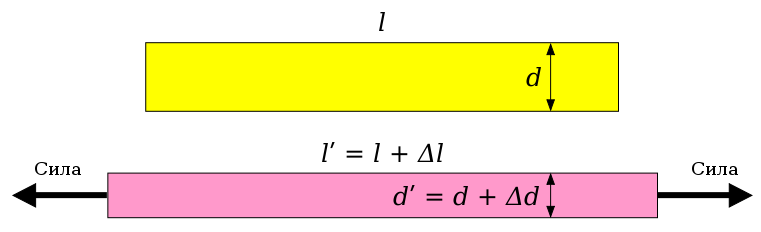
Пусть l и d длина и поперечный размер образца до деформации, а l¢ и d¢ – длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l¢–l), а поперечным сжатием – величину, равную (d¢–d). Если (l¢–l) обозначить как Δl, а (d¢–d) как Δd, то относительное продольное удлинение будет равно величине Δl/l, а относительное продольное сжатие – Δd/d. Тогда в принятых обозначениях коэффициента Пуассона имеет вид: μ= –Δd/d ˣ l/Δl.

Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых – 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, т.е. объем стального тела увеличивается при растяжении. Для резины (эластомеров) он равен приблизительно 0,5, т.е. изменения в объеме практически не происходит.

Вязкость – мера сопротивления течению. Она является основным свойством для жидких тел, а также для пластичных тел после превышения предела текучести.

Упругость – способность тела после деформирования полностью восстанавливать свою первоначальную форму или объем, т.е. работа деформирования равна работе восстановления. Упругость тел при растяжении – сжатии характеризуется модулем упругости первого рода (модуль Юнга) Е [Па], а при сдвиге – второго рода (модуль сдвига) G [Па].

Пластичность – способность тела под действием внешних сил необратимо деформироваться без нарушения сплошности. В реологии в этом смысле при деформациях существует понятие «предельное напряжение сдвига» (ПНС). Это напряжение, при превышении которого в материале появляются пластические деформации.

Прочностью называют сопротивление тела действию внешних сил, которые приводят к разрушению. У гуковских (упругих) тел скорость деформации не влияет на предел прочности, так что различий в статической и динамической прочности не существует. У негуковских тел (к которым принадлежат, например, почти все твердые пищевые продукты), которые обладают как упругими, так и пластичными (вязкими) свойствами, прочность зависит от скорости деформирования.

Каждый материал обладает всем комплексом реологических свойств, хотя и в различной степени. У одного и того же материала в зависимости от его состояния и условий нагружения, могут проявляться, в большей или меньшей степени, различные реологические свойства.

Итак, реология описывает деформацию тела под действием напряжения и с этой точки зрения позволяет разделить тела на твердые (упругие) и жидкообразные(текучие).

Идеально твердое тело деформируется упруго. Энергия, необходимая для этой деформации, полностью возвращается при снятии напряжения.

Идеально текучие системы, такие как жидкости или газы, де­формируются необратимо – они текут. Энергия, необходимая для их деформации, переходит в теплоту, рассеивается и не может быть возвращена простым снятием напряжения. В то время как твердые тела и жидкости деформируются под действием напряжения различным образом, между жидкостью и газом в принципе не наблюдается различий в их реологическом поведении. Различие между жидкостью и газом проявляется лишь в том, что при повышении температуры вязкость жидкости падает, а вязкость газа - растет.

Но, реальные тела, с которыми мы обычно встречаемся, никогда не являются ни идеально твердыми, ни идеально жидкими. Например, реальные твердые тела под действием силы достаточной величины также могут деформироваться необратимо, они “ползут” или “текут”. Так сталь, типичное твердое тело, можно заставить “течь”, например, в процессе прессования стального листа при производстве деталей автомобильных кузовов.

Только очень немногие жидкости, имеющие практическое значение, близки по своему поведению к идеальным. Подавляющее большинство жидкостей по их реологическому поведению можно отнести к промежуточной области между жидкостью и твердым телом: они проявляют как вязкие, так и упругие свойства, и поэтому могут быть названы “вязкоупругими”.

Деление материалов по их реакции на приложенные напряжения на твердые и жидкообразные должна быть расширена введением шкалы времени для любого процесса деформации.

С одной стороны, для всех материалов может быть определен характеристический фактор времени (так называемое время релаксации), определяющий реакцию материала на прикладываемое напряжение, который является бесконечной величиной для идеально упругого твердого тела и почти равен нулю для жидкостей, подобных воде ( λ =10^-12 с).

С другой стороны, деформационные процессы протекают в течение определенного времени t.Отношение этих двух времен (так называемое число Деборы D=(λ/t)также определяет будет ли тело считаться твердым или жидким. Высокое значение числа D характерно для твердых тел, а низкое – для жидкообразных.

Чтобы лучше это понять, рассмотрим два примера.

1. Если воду подавать из сопла с очень большой скоростью, ее капли, ударяясь о твердую стенку, будут сплющиваться. Затем эти капли упруго отскакивают и их сферическая форма мгновенно восстанавливается. При этих экстремально быстрых процессах t,будучи очень малым, определяет очень высокое число Деборы. Это означает, что даже вода может реагировать на деформации как упругое тело.

2. Знаменитые стеклянные окна Шартрского кафедрального собора во Франции имеют “подтеки”, так как они были сделаны около 600 лет тому назад. В средние века оконные стекла имели вверху и внизу одинаковую толщину, но к нашему времени молекулы стекла под влиянием силы тяжести “стекли” вниз. Поэтому сейчас толщина стекла в верхней части близка к толщине бумаги, в то время как в нижней она увеличилась более чем в два раза. В результате очень длительного периода времени t процесса течения число Деборы стало малым. Таким образом, можно утверждать, что твердое стекло, несмотря на высокое значение λ при комнатной температу­ре, в условиях, описанных выше, можно отнести к жидкостям... если ждать достаточно долго!

Из концепции числа Деборы вытекает важный вывод: такие вещества, как вода или стекло, не могут быть безоговорочно отнесены к жидкостям или твердым телам. При определенных напряжениях и в зависимости от периода времени воздействия этих факторов они ведут себя либо как жидкие, либо как твердые тела.

Приборы, которые измеряют вязкоупругие характеристики твердых тел, твердообразных систем и жидкостей, называют “реометрами”. Приборы, применение которых ограничено исследованиями вязкого течения жидкостей, обычно называют “вискозиметрами”.

Основной закон вискозиметрии, описывающий течение идеальной жидкости, впервые сформулировал Исаак Ньютон:

τ=η 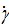(1)

где τ- напряжение сдвига; η- вязкость; - скорость сдвига.

Вязкостьпредставляет собой коэффициент пропорциональности между напряжением и скоростью сдвига, физический смысл которой - сопротивление жидкости любому необратимому изменению положения элементов ее объема. Чтобы поддерживать течение жидкости, необходимо постоянно затрачивать энергию.

Сдвиг, вызывающий течение жидкости, можно описать четырьмя модельными случаями.

Течение между двумя плоскопараллельными пластинами осуществляется в том случае, когда одна пластина движется, а другая неподвижна. Это вызывает ламинарное течение слоев, подобное смещению отдельных карт в колоде.

Течение в кольцевом зазоре между двумя концентрическими цилиндрами, из которых один неподвижен, а другой вращается. В этом случае течение может быть представлено как перемещение концентрических слоев, размещенных таким образом, что каждый последующий слой находится внутри предыдущего.

Течение в трубопроводах, трубках или капиллярах. Течение жидкости через капилляр реализуется вследствие разности давлений на входе в капилляр и на выходе из него. При этом имеет место параболическое распределение скоростей слоев в радиальном направлении внутри потока жидкости.

Течение между двумя параллельными плоскостями или между конусом и плоскостью. В этом случае одна из рабочих поверхностей неподвижна, а другая вращается. Такое течение может моделироваться вращающейся цилиндрической стопкой монет, в которой каждая последующая монета смещена на малый угол относительно предыдущей.

Давайте разберемся с определением напряжения и скорости сдвига с помощью модели параллельных пластин (рис. 1).

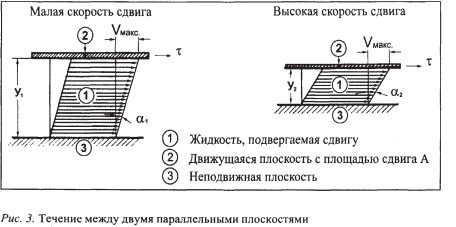Рис.1.Течение между двумя параллельными плоскостями.

Напряжение сдвига

Сила F,приложенная к площади А, находящейся на границе раздела верхней плоскости и жидкости под ней, вызывает течение в слое жидкости. Индуцируемое напряжение сдвига определяется как

τ= 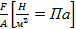(2)

Единица “паскаль” введена вместо единицы “дин/см²”, которую применяли раньше, особенно в научной литературе, как размерность напряжения. Соотношение между этими единицами следующее:

1 Па = 10 дин/см².

Скорость сдвига

Напряжение сдвига t вызывает характерную картину послойного распределения скоростей в слое жидкости. Максимальная скорость течения V_макс наблюдается у границы раздела жидкости с движущейся плоскостью.

По мере удаления от подвижной плоскости скорость течения снижается, и на расстоянии у от нее, на границе с неподвижной плоскостью, V_макс= 0.

Ламинарное течение означает, что слои жидкости бесконечно малой толщины скользят один по другому подобно отдельным картам в колоде. Один ламинарный слой смещается по отношению к другому на некоторую часть общего сдвига всего слоя жидкости между обеими плоскостями. Градиент скорости поперек зазора называют “скоростью сдвига”, которая математически выражается в виде дифференциала:

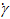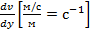= (3)

В случае двух параллельных плоскостей с линейным градиентом скорости поперек зазора дифференциал в этом уравнении приводится к виду

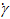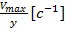= (4)

Точка над g указывает на то, что скорость сдвига есть производная по времени от деформации, обусловленной напряжением сдвига, воздействующим на тонкий ламинарный слой жидкости:

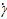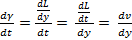= (5)

т. е. уравнения (3) и (5) идентичны. Уравнение (1) может быть переписано с использованием уравнения (5):

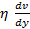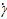τ= = η (6)

Итак, сдвиговое напряжение в жидком теле пропорционально скорости развития деформации. Это и означает, что жидкие тела текут.

Идеально твердые тела деформируются под воздействием сдвиговых напряжений (рис. 2) в соответствии с законом Гука:

τ=G 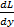= Gtgy≈Gγ ,(7)

где t - напряжение сдвига = сила/площадь, [Н/м² = Па]; G- модуль упругости, который связан с жесткостью твердого тела, [Н/м²], γ-относительнаядеформация (безразмерная величина); у - высота твердого тела, [м]; ∆L- абсолютная деформация тела в результате воздействия сдвигового напряжения, [м].

Модуль упругости в этом уравнении является корреляционным коэф­фициентом, характеризующим жесткость, который связан главным образом, с физико-химической природой данного твердого тела. Он определяет сопротивление твердого тела деформации.

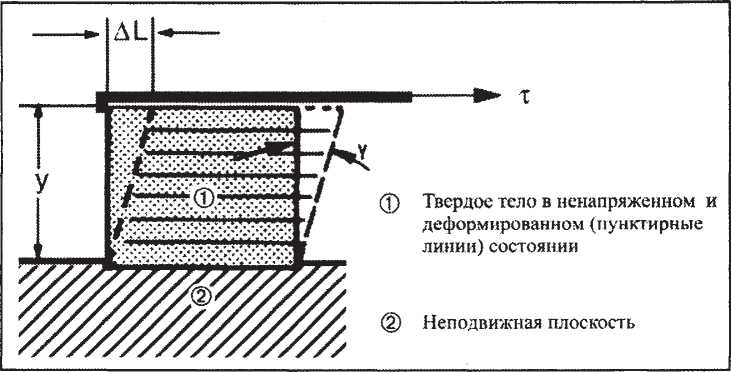Рис. 2. Деформация твердого тела.