Техника построения контрольных карт

1. Построение контрольных карт по количественному признаку. К этому типу карт относятся: Х-карта, 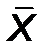-карта, R-карта, S-карта и совмещенные их комбинации. Построение контрольных карт этого типа осуществляется по общепринятому алгоритму. Изложим его на примере построения контрольной 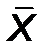-карты. Исходные данные: измеряемые величины по каждой выборке i, i=1,…,N, обозначенные как 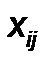.Для построения контрольной 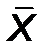– карты потребуется осуществить следующие расчетные и графические процедуры.

Шаг 1. Построить гистограмму распределения переменной ( 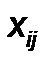) и определить статистический закон распределения. В зависимости от вида закона распределения случайной переменной используются соответствующие ему формулы для расчета верхнего и нижнего контрольного предела [9,12,19].

Шаг 2. Рассчитать по каждой выборке i=1,2,…,N среднее значение по количеству измерений одной выборки (M), а именно,

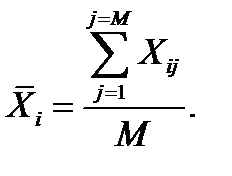(13.2)

Шаг 3. Построить линейный график средних значений 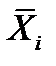и в последующем использовать его для построения контрольной карты (рис. 8.2).

Шаг 4. Рассчитать среднее значение средних по выборке величин 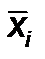как

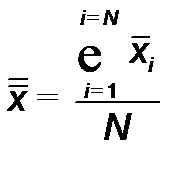, (13.3)

и принять полученную величину 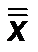как координату ЦЛ контрольной карты.

Шаг 5. Выполнить расчет координат ВКП и НКП по вариантам и нанести их на график. Если гистограммой подтверждается гипотеза о нормальном законе распределения измеряемой случайной величины, то величину ВКП и НКП следует определять по формуле

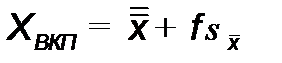,(13.4)

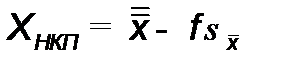, (13.5)

где 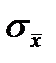– среднеквадратичное отклонение 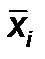, i =1,2,….N; f – коэффициент жесткости границ.

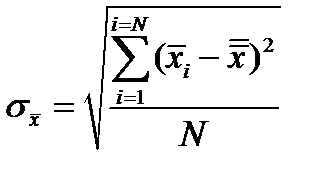. (13.6)

На практике коэффициент жесткости допустимых колебаний измеряемой величины f принимается равным числам1, 2 или 3,и в результате образуются стандартные зоны допустимых колебаний показателей:

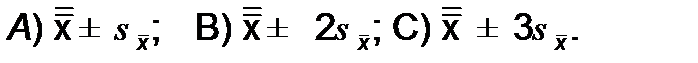(13.7)

Шаг 6. Нанести на линейный график ЦЛ = 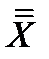и линии ВКП = X_ВКП и НКП = X_НКП в соответствии со значениями f, завершить построение контрольной 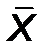- карты и перейти к анализу и оценке качества продукции.

Важным дополнением к контрольной 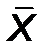-карте является построение карты размаха измеренных величин в выборке, т.е. R-карты. Эта карты, как правило, совмещается с контрольной 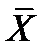-картой, раскрывая уровень разброса величин, составляющих некоторую среднюю величину. Размах значений R_i определяется как разность между максимальным и минимальным значениями отклонения j – ой случайной величины по выборке i:

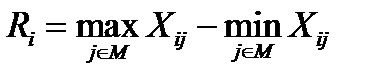(13.8)

Алгоритм построения контрольной R-карты включает аналогичные процедуры, составляющие алгоритм построения 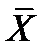- карты. В качестве исходной переменной величины используется величина размаха R_i , i, i=1,…,N. Для удобства последующего анализа качества продукции и процессов контрольные 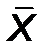- карту и R-карту совмещают, строят одна под другой с одинаковым масштабом горизонтальных осей (рис. 13.7).

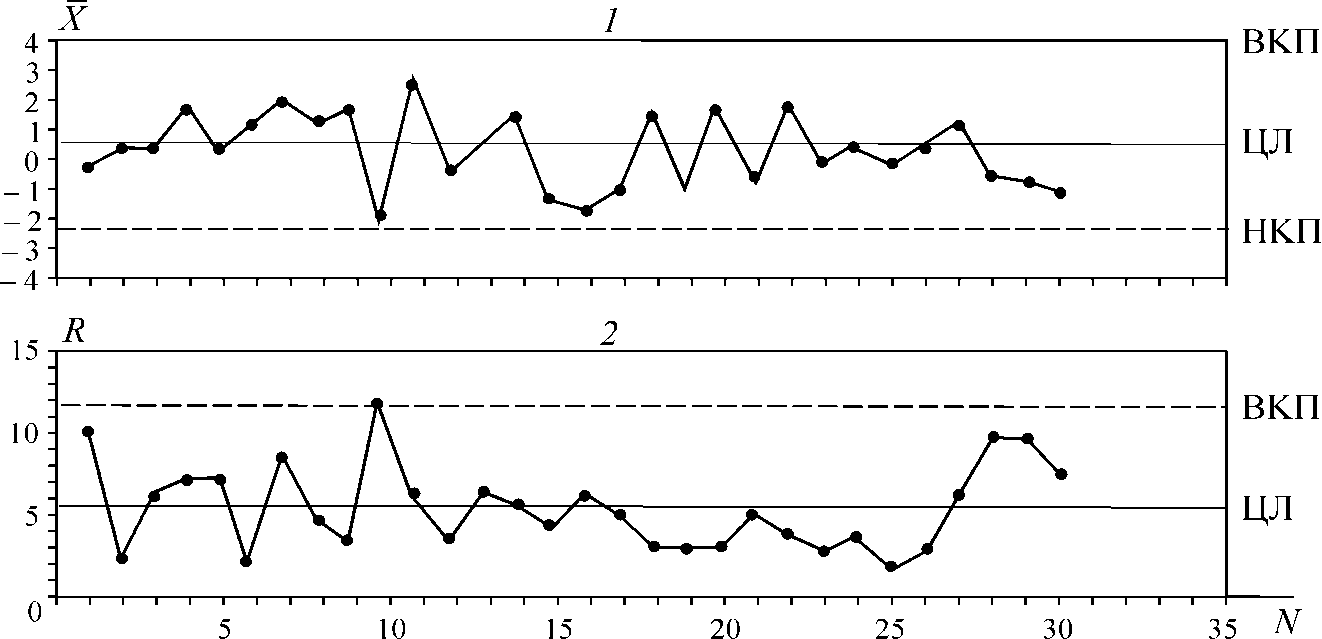
Рис. 13.7. Фрагмент 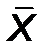– карты (1) и R– карты (2) и их совмещение

2. Построение контрольных карт по альтернативному признаку.

К этому типу карт относят: C-карта, U-карта np –карта и р – карта. Исходные данные: регистрируемое количество дефектов в партии продукции i, i=1,…,N, или в количестве продукции, произведенной в день, на один станок или 100 единиц оборудования.Основная особенность исходной информации – равные объемы выборок данных.

Построения контрольной С-карты ведется по алгоритму близкому по последовательности и содержанию шагов, как и при построении 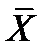– карты. Центральная линия определяется значением средней арифметической величины числа дефектов по каждой выборке :

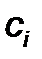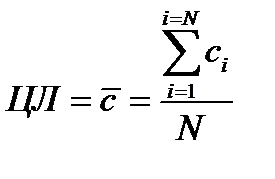(13.9)

Особенность проявляется при расчете среднеквадратичного отклонения (шаг 5).Гистограмма числа дефектов по выборкам описывается распределением Пуассона, то среднеквадратичное отклонение 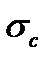определяется по формуле:

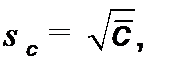(13.10)

Верхний и нижний контрольные пределы по зонам уровня качества определяются как:

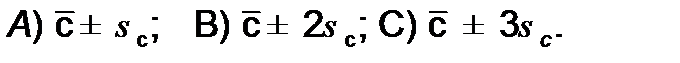(13.11)

Графическое отображение С-карты подобное как на рис. 13.7.

Контрольная U-карта служит для отображения изменения среднего числа дефектов

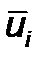, приходящихся на единицу продукции по выборке (партии) n_i, i=1,…,N при условии неравенства объемов выборок ( n₁ ≠ n₂ ) . Переменная ( 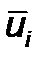) по каждой выборке ( n_i), рассчитываемое по формуле:

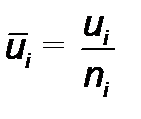, (13.12)

Центральная линия определяется по формуле:

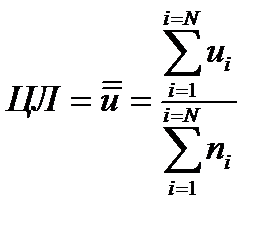.(13.13)

В связи с принятой гипотезой о законе распределения переменной 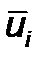аналогичной, что и для количества дефектов по выборкам, то среднеквадратичное отклонение определяется по формуле вида (13.10), а допустимые пределы колебания анализируемой величины по формуле (13.11).

Контрольная np-карта служит для отображения изменения числа дефектов 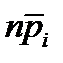по выборкам (партиям) i, i=1,…,N, при условии равенства объемов выборок, большом количестве дефектов (более 5%) и биномиальном распределении переменной величины.

Центральная линия, определяющая среднее число дефектных изделий ( 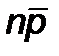) для N-го количества выборок, и пределы допустимых колебани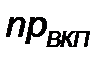й и 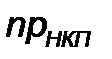рассчитываются по формулам, аналогичным (13.9) и (13.11). Особенность проявляется при расчете среднеквадратичного отклонения в связи с изменением характера распределения анализируемой случайной величины. Гистограмма распределения числа дефектов по выборкам описывается биномиальным законом, и среднеквадратичное отклонение 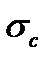определяется по формуле вида:

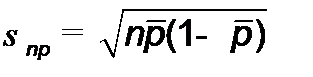, (13.14)

где 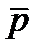- средняя доля дефектных (бракованных) изделий.

Контрольная р-карта служит для установления характера изменения доли дефектов р_i в выборке (партии) i, i=1,…,N при условии меняющегося объема выборок. Для выборок с большой долей дефектов для обработки данных используется биномиальное распределение, с малой долей дефектов – распределение Пуассона. Расчет параметров р – карта осуществляется по тому же алгоритму, что и параметров U-карты и np –карта.

Вопросы для контроля знаний

1. Какие отличительные особенности характерны для статистического управления качеством?

2. Какие методы включены в элементарные методы статистического контроля качества?

3. В чем заключается сущность метода «расслоения» при анализе и оценке качества продукции?

4. Какое правило положено в основу построения диаграммы Парето?

5. Какие правила положены в основу построения причинно-следственной диаграммы?

6. Какие условия определяют применение метода «разброса» для оценки качества?

7. Какой природы регрессионные зависимости наблюдаются между характеристиками качества продукции?

8. Какова цель построения гистограмм при анализе качества продукции?

9. Какие модели гистограмм используются для анализа и оценки качества?

10. Как изменяется положение кривой нормального распределения при изменении параметров 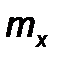и s ?

11. Какие элементы отличают контрольную карту от линейного графика?

12. Каким образом связано определение ординаты контрольных пределов карты с законами распределения вероятностей измеряемой величины или фиксируемого события?

13. Какие признаки положены в основу типизации контрольных карт?

14. Какие контрольные карты используются для анализа качества по измеряемой характеристики качества?

15. Какие основные контрольные карты используются для анализа качества по альтернативному признаку?