Аппроксимация на основе специальных рядов
| Математика, подобно жернову, перемалывает то, что под нее засыпают, и, засыпав лебеду, вы не получите пшеничной муки, так, исписав целые страницы формулами, вы не получите истины из ложных посылок. Т. Гексли. |
Типовые ряды, известные из математического анализа (ряды Тейлора, Фурье), не подходят для описания функций распределений, так как не обладают свойствами, присущими этому виду функций. Для подобного описания предложены специальные функции, например, основанные на полиномах Чебышева – Эрмита. К числу таких функций относится ряд Грама – Шарлье
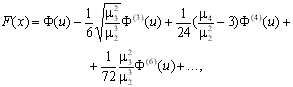
| (5.1) |
где Ф(u) – функция нормального распределения центрированной и нормированной случайной величины u=(х–m1)/m20,5, Ф(k)(u) – k-я производная от функции нормального распределения.
Вычисление Ф(u) не требует численного интегрирования, так как имеются ее приближения на основе полиномов, а производные представимы элементарными функциями:
| Ф(3)(u)=(u2–1) fн(u), Ф(4)(u)=(– u3+3u) fн(u), Ф(6)(u)=(–u5+10u3–5u) fн( u ), fн(u)= (2p)–0,5 exp(–u2/2). | (5.2) |
Ряд Грама – Шарлье целесообразно использовать для описания распределений, близких к нормальному. В других случаях начинают проявляться серьезные недостатки: ряд может вести себя нерегулярно (увеличение количества членов ряда иногда снижает точность аппроксимации); ошибки аппроксимации возрастают с удалением от центра распределения; сумма конечного числа членов ряда при большой асимметрии распределения приводит к отрицательным значениям функций, особенно на краях распределений. Этот ряд применяют только при весьма умеренном коэффициенте асимметрии, не превышающем 0,7. Следовательно, применение рядов тоже не обеспечивает необходимой общности решения задач аппроксимации.
Пример 5.1.Оценить качество аппроксимации ЭД, табл. 2.4, на основе ряда Грама – Шарлье. Проверку согласованности провести с использованием критерия хи-квадрат при уровне значимости a = 0,05.
Решение. В примере 2.3 были вычислены значения оценок моментов:
m1 =27,508, m2 = 0,913, m3 = 0,132, m4 =1,819.
На основе табл. 2.4 построим табл. 5.3.
Таблица 5.3
| i | ||||||
| ni | ||||||
| Верхняя граница, xi | 26,37 | 26,95 | 27,53 | 28,11 | 28,69 | бесконечность |
| F(xi) | 0,127 | 0,303 | 0,517 | 0,721 | 0,877 | |
| DFi | 0,127 | 0,176 | 0,214 | 0,204 | 0,156 | 0,123 |
| Fi | 5,588 | 7,744 | 9,416 | 9,976 | 6,864 | 5,412 |
| ( ni–Fi)2/Fi | 0,062 | 0,204 | 0,036 | 0,000 | 0,506 | 0,063 |
В таблице значения функции распределения F(xi) для верхней границы интервала и теоретическое значение оценки вероятности DFi попадания случайной величины в i-й интервал вычислены на основе ряда Грама – Шарлье. Обозначения оценки частоты попадания Fi=DFin случайной величины в i-й интервал, вероятности DFi попадания случайной величины в интервал xi – xi–1, взвешенного квадрата отклонения (ni–Fi)2/Fi аналогичны табл. 3.2. Сумма взвешенных квадратов отклонения c2=0,872 (критическое значение составляет 7,815).
Выборка имеет слабо выраженную асимметрию. По сравнению с аналогичным значением c2=1,318 при аппроксимации ЭД нормальным распределением, ряд Грама – Шарлье дает более "точное" описание данных
Дата добавления: 2017-10-04; просмотров: 1536;











