Свободная энергия (потенциал) Гельмгольца

F = U – TS; после дифференцирования получим:

dF = dU – TdS – SdT; вспоминая, что TdS= dU+ dA +ε,

получим: dF=dA–SdT=–SdT–pdV–ε.(24)

Если T, V = const и ε → 0,

Стремление функции «свободная энергия Гельмгольца» к минимальному значению указывает на приближение системы к равновесию. Условие равновесия: ΔF = 0 (25)

Свободная энергия (потенциал) Гиббса

G = U–TS + pV = H–TS;

dG = dU – TdS – SdT + pdV + Vdp. Выполнив аналогичное преобразование,

получим: dG = –SdT + Vdр– ε. приT, р= const и ε → 0(26)

Стремление функции «свободная энергия Гельмгольца» к

минимальному значению указывает на приближение системы к равновесию. Условие равновесия: ΔG = 0 (27)

Произведение TS характеризует связанную с частицами свободную энергию, т.е. ту часть полной энергии системы, которая рассеивается в окружающую среду в виде теплоты; это – «потерянная работа».

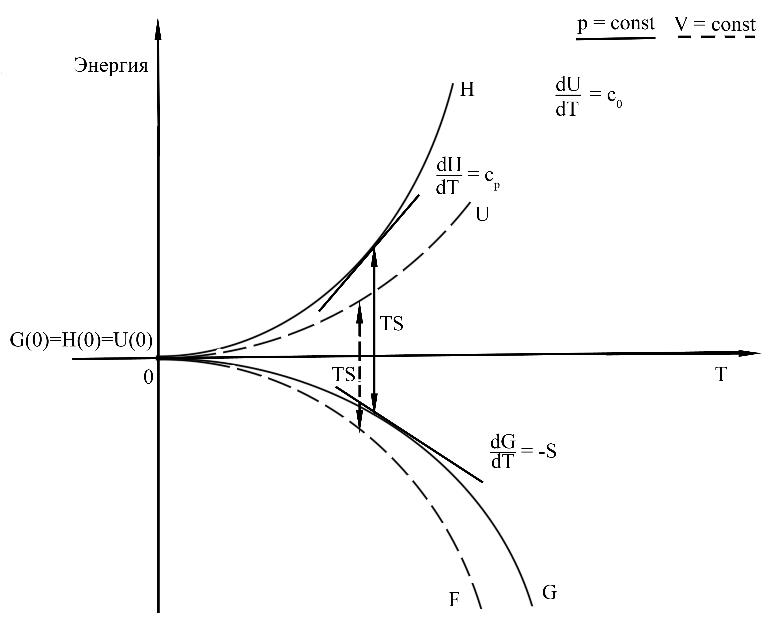
Диаграмма Кирдеева

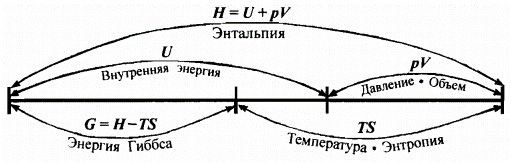
Следовательно, энергия Гиббса и энергия Гельмгольца характеризуют ту часть полной энергии системы, которая может быть превращена в работу в изобарно-изотермическом или изохорно-изотермическом процессах соответственно (так называемая полезная работа, совершаемая системой). В этом состоит физический смысл величин G и F. Энергия Гиббса и энергия Гельмгольца – функции состояния системы, их абсолютные значения не поддаются вычислению. Для одного моля чистого вещества потенциал Гиббса равен химическому потенциалу вещества:

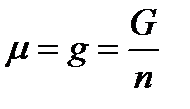(28)

Подобно другим термодинамическим параметрам и функциям, характеризующим состояние системы, изменение энергии Гиббса в результате любого процессаопределяется только начальным и конечным состоянием системы, независимо от пути процесса.

DG =G_кон-G_нач (29)

Для полной энергетической характеристики вещества при стандартных условиях используют стандартную энергию Гиббса образования вещества ΔG˚, значение которой дано в справочной литературе. Для простых веществ в термодинамически устойчивой форме стандартная энергия Гиббса их образования условно принята равной нулю.

Термодинамический критерий равновесия

Если G=G_min , (энергия Гиббса имеет минимальное значение) и DG = 0система находится в состоянии термодинамического равновесия.

Применение этой функции к решению практически важных вопросов расчета равновесия, как предельно достижимого состояния реагирующих систем, требует некоторого дополнительного исследования термодинамического потенциала и его вычисления.

Для обратимых процессов или условия равновесия можно определить значения частных производных термодинамического потенциала:

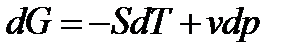
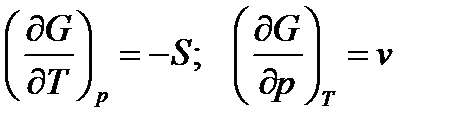или

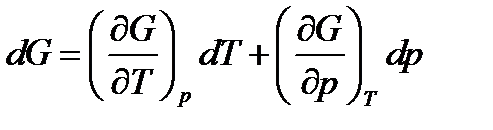. (30)

Таким образом, термодинамический потенциал может быть рассчитан для 1 моля вещества, так же как и энтропия, так как частная производная от термодинамического потенциала по давлению, при условии постоянной температуры, равна молярному объему.

Термодинамический потенциал системы, состоящей из ряда компонентов, будет суммироваться по всем компонентам с учетом их взаимного влияния (концентрация или активность). Поэтому полный дифференциал термодинамического потенциала системы можно записать следующим образом:

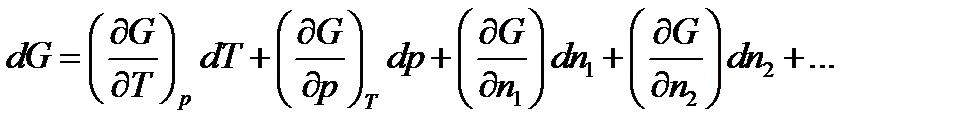(31)

где n₁, n₂ и т.д. – числа молей компонентов системы.

В общем случае при наличии в системе необратимых процессов на основании уравнения (26) этот же полный дифференциал равен:

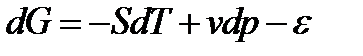
Сопоставляя уравнения между, можно установить условия равновесия в системе при T = constи p = const:

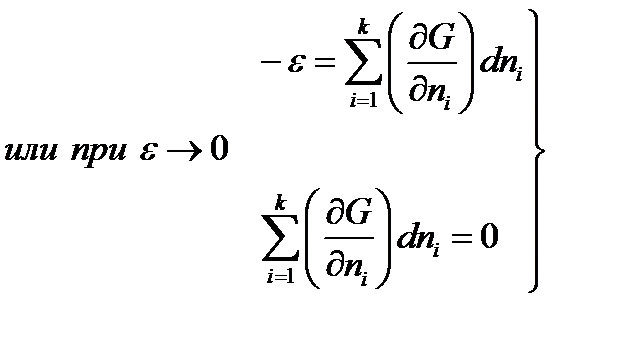(32)

Таким образом, при условии p, T = const необратимость системы зависит от изменения числа молей компонентов в химически реагирующей системе, а в момент равновесия изменения числа молей непроисходит.

Изменение энергии Гиббса в результате химической реакции при стандартных условиях вычисляют по уравнению:

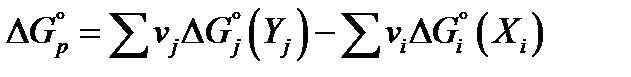(33)

где 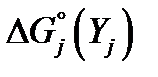, 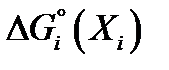– стандартные энергии Гиббса продуктов реакции Y_j и исходных веществ X_i; v_j и v_i– соответствующие стехиометрические коэффициенты в уравнении химической реакции.

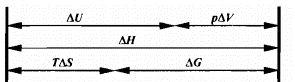
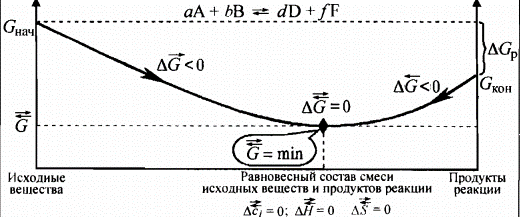
Проводя аналогию с диаграммой Кирдеева при T, р = const, получим

DG_р= G_кон -G_нач = DH-TDS (34)

В закрытой системе знак изменения энергии Гиббса является критерием направленности самопроизвольного процесса при проведении его в изобарно-изотермических условиях:

- при DG_р = 0 (G=G_min ,энергия Гиббса имеет минимальное значение) система находится в состоянии термодинамического равновесия;

- приDG_р< 0 (G>G_кон , энергия Гиббса убывает) процесс самопроизвольно протекает в прямом направлении, т.е. термодинамически возможен; критерий ничего не говорит о скорости процесса и необходимых условиях для его начала;

- при G_р> 0 (G<G_кон), энергия Гиббса возрастает) самопроизвольно протекает только обратный процесс, прямой процесс термодинамически невозможен

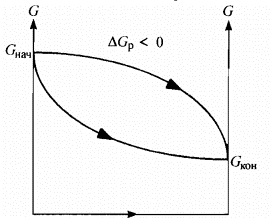возможна прямая реакция, идущая до конца

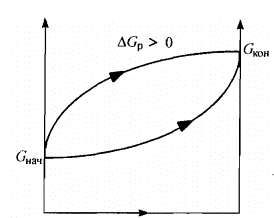прямая реакция невозможна

В системе при р = const, T = соnst самопроизвольно могут совершаться только такие процессы, в результате которых G уменьшается, DG < 0(Еще одна формулировка 2-го закона термодинамики).

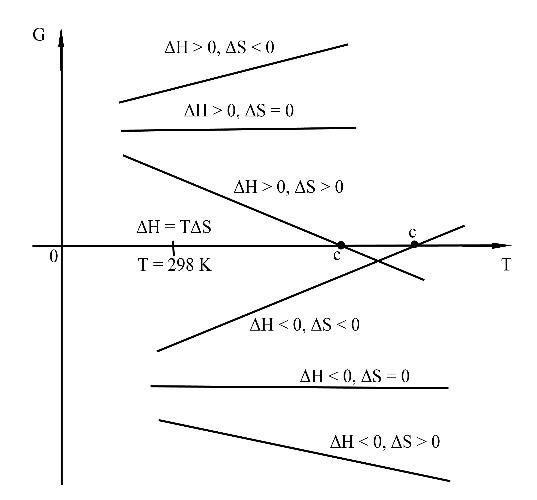
Ситуация изменится, если Т = var.

Cистема находится в равновесии (ΔG = 0) при любой температуре, если ΔН= TΔS. Запрещенные процессы – выше оси температур, разрешенные располагаются ниже оси.

DG

.

…………………………………………………………..

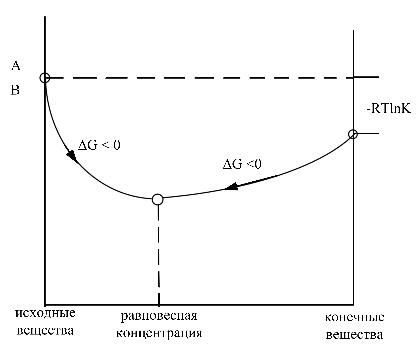
Продолжение следует!!!!!

В закрытой системе знак изменения энергии Гиббса является критерием направленности самопроизвольного процесса при проведении его в изобарно-изотермических условиях:

- при DG = 0 (G = G_min ,энергия Гиббса имеет минимальное значение) система находится в состоянии термодинамического равновесия;

- при DG < 0 (G < G_min , энергия Гиббса убывает) процесс самопроизвольно протекает в прямом направлении, т.е. термодинамически возможен; критерий ничего не говорит о скорости процесса и необходимых условиях для его начала;

- при G > 0 (G > G_min, энергия Гиббса возрастает) самопроизвольно протекает только обратный процесс, прямой процесс термодинамически невозможен.

Чем больше значение энергии Гиббса в начальном состоянии по сравнению с конечным, тем больше химическое сродство между реагентами в рассматриваемой системе. Если при заданных условиях реакция не идет до конца, равновесный состав системы определяется константой равновесия.

Композиционные материалы – это многокомпонентные гетерогенные термодинамические системы с развитой сетью границ, в которых микроскопические параметры, порождающие поверхностные явления, начинают значительно влиять на энергетику макропроцессов.