Внутренняя энергия газа

Под термином внутренняя энергия понимают особую форму энергии, обусловленную тепловым движением молекул. Внутренняя энергия тела равна сумме потенциальной и кинетической энергии его молекул (энергию связи ядер атомов к внутренней не относят).

В случае идеального газа потенциальная энергия, обусловленная взаимодействием между молекулами, равна нулю и поэтому внутренняя энергия идеального газа равна сумме кинетических энергий поступательного и вращательного движений его отдельных молекул.

Молекулы реальных газов взаимодействуют между собой, поэтому внутренняя энергия реального газа, кроме суммы кинетических энергий поступательного и вращательного движений отдельных молекул, включает в себя и потенциальную энергию взаимодействия молекул между собой.

Для оценки средней кинетической энергии 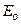отдельных молекул идеального газа Больцман ввёл понятие числа степеней свободы ( 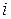) отдельной молекулы. Оно равно числу независимых (невыражаемых друг через друга) координат, характеризующих движение молекулы в пространстве. Поступательное движение молекул характеризуют тремя степенями свободы (х, у, z), вращательное движение - также тремя степенями свободы (вращение молекулы вокруг осей 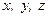, выходящих из её центра масс); кроме того, молекулы имеют ещё колебательные степени свободы, обусловленные колебаниями атомов внутри молекулы. Число колебательных степеней свободы может быть очень велико, но, при нормальных условиях, эти степени свободы можно не учитывать.

Момент инерции шара

Для одноатомных молекул число степеней свободы i =3, так как энергия их вращательного движения 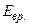пренебрежимо мала по сравнению с энергией их поступательного движения 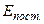. Действительно:

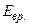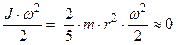= (так как ).

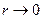Для двухатомных молекул 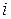=3+2=5 (три поступательные и две вращательные степени свободы, так как энергия вращательного движения вокруг третьей оси, соединяющей атомы, пренебрежимо мала из-за того, что ).

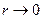Для трёхатомных и более сложных молекул 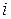=3+3=6 (три поступательные и три вращательные степени свободы).

Теорема Больцмана: ввиду полной хаотичности теплового движения молекул все виды их поступательного и вращательного движений равновероятны, поэтому на каждую степень свободы молекулы приходится в среднем одинаковая энергия.

Согласно этой теореме и уравнению Больцмана, на одну степень свободы молекулы одноатомного газа в среднем приходится энергия:

.

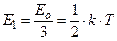Поэтому, полная средняя кинетическая энергия молекулы газа, имеющей i степеней свободы:

= .

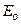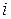
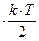Тогда внутренняя энергия любой массы m идеального газа:

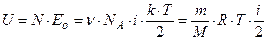(так как ).

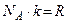Итак: = .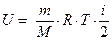

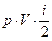Так ли уж велика внутренняя энергия тела? Рассмотрим это на примере. Рассчитаем внутреннюю энергию 1 м³ воздуха (для которого 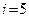, так как основные компоненты воздуха – газы 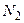и 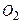) при нормальных условиях:

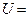
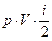
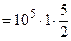
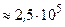Дж.

Много ли это? Рассчитаем, на какую высоту h надо поднять бетонную плиту массой m = 1т = 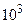кг, чтобы она обладала такой же энергией:

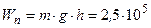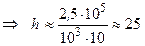Дж м.

Теплоёмкость

Это количество теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1 градус. Такое же количество тепла тело отдаёт при остывании на 1^o. Теплоёмкость единицы массы вещества называется удельной, а теплоёмкость 1моля - молярной теплоёмкостью этого вещества. Согласно определению, выражение для расчёта теплоёмкости имеет вид: .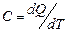

Теплоёмкости различных веществ сильно отличаются друг от друга. Так, удельная теплоёмкость воды при 20^о С составляет 4200, дерева - 1700, воздуха - 1010, алюминия - 880, железа - 460, меди - 385, свинца - 130 Дж/кг×К. Удельная теплоёмкость слабо растёт с температурой (при 90^о С теплоёмкость воды составляет 4220 Дж/кг×К) и сильно меняется при фазовых превращениях вещества (т.е. при изменении его агрегатного состояния): теплоёмкость льда при 0^оС в два раза меньше, чем воды; теплоёмкость водяного пара при 100^оС около 1500 Дж/кг×К.

В соответствии с законом сохранения энергии, теплота 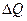, передаваемая телу (газу), расходуется на увеличение его внутренней энергии 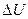и на совершение телом (газом) работы A (первое начало термодинамики):

DQ=DU + A ,

где работа газовой системы (тела) .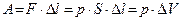

Теплоёмкость зависит от условий, в которых происходит изменение температуры тела. Для изохорического процесса имеем: DV = 0 Þ А = 0. Тогда молярная теплоёмкость (n= 1 моль) при постоянном объёме равна:

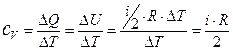Þ . (*)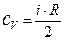

При нагревании же газа при постоянном давлении (p=const) объём газа изменяется, поэтому подводимое тепло расходуется не только на увеличение внутренней энергии газа, но и на совершение им работы. Тогда молярная теплоёмкость при постоянном давлении равна:

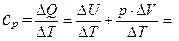
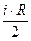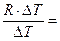
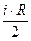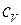+ +R= +RÞ

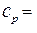
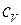+ R(Уравнение Майера) (**)

Из уравнения (**)следует, что физический смыслуниверсальной газовой постоянной Rсостоит в том, что она равна работе, совершаемой 1молем идеального газа при его изобарическом нагревании на 1 градус.

Отношение 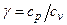представляет собой величину, характерную для каждого газа и определяемую только числом степеней свободы 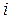молекул газа:

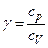
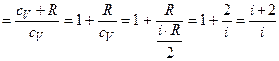Þ .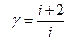

Таким образом, измерение теплоёмкости тела позволяет определить число степеней свободы - микроскопической характеристики молекул тела.

Однако при низких и высоких температурах экспериментальные значения 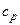и с_V существенно отличаются от их теоретических значений, рассчитанных по формулам, учитывающим не только поступательные и вращательные, нои колебательные степени свободы: при низких Т получили 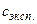<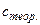; при высоких Т- 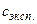>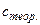. Это происходит вследствие того, что при низких Т имеет место "вымораживание" степеней свободы (колебательных), а при высоких Т - "возбуждение" новых (колебательных) степеней свободы.