Стремление энтропии системы к максимальному значению (условие экстремума) указывает на приближение системы к равновесию.

Следовательно, в изолированной системе знак изменения энтропии является критерием направленности самопроизвольного процесса:

Если ΔS=0, то S=S_max; система находится в состоянии термодинамического равновесия (параметры состояния во времени не изменяются)

Если ΔS>0, тоS→S_max, (энтропия растет)- процесс самопроизвольно протекает в прямом направлении, т.е. термодинамически возможен.

Если ΔS<0, то S→S_min, (энтропия убывает)– самопроизвольно может развиваться только обратный процесс, прямой процесс т/д невозможен.

Только возрастанием энтропии можно объяснить самопроизвольное протекание в изолированных системах таких процессов, как передача теплоты от более нагретого тела к менее нагретому, или взаимная диффузия (смешение) двух или нескольких химически не взаимодействующих газов.

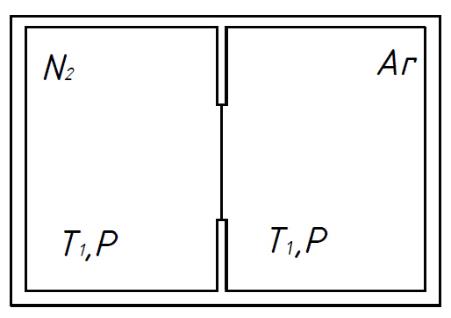
Объединим две различные изолированные системы в одну (состояние 1). Пусть р, Т, U, V = const, но нашелся «волшебник», который проник внутрь изолированной системы и разрушил перегородку.

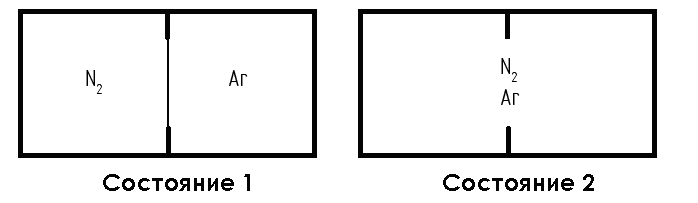Схема смешения двух химически не взаимодействующих газов, процесс 1→2

«Самопроизвольным, или спонтанным, является про­цесс, который совершается в системе без затраты ра­боты извне и который уменьшает работоспособность системы после своего завершения»

Химическая термодинамика изучает системы, состоящие из большого числа частиц, неизбежно вступающие во взимодействие– макросистемы. В подобных системх различают так называемые макро- и микропараметры. Для каждой индивидуальной частицы характерно микросостояние, которое описывается микропараметрами (координаты в пространсте, векторы скорости, энергия). Совокупность микропараметров каждой частицы называется микросостоянием частицы.

К макрохарактеристикам относятся независимые переменные, свойственные системе в целом (давление (р), объем (V), температура (T), концентрации веществ (c_i), которые определяются экспериментально или рассчитываются теоретически.

Для описания системы на таком уровне потребовалась новая характеристика – термодинамическая вероятность состояния частицы.

Термодинамическое вероятностное состояние – число микросостояний, посредством которых реализуется данное макросостояние системы. В отличие от математической вероятности, которая может принимать значения от нуля до единицы, термодинамическое вероятность представляет собой очень большую величину, дополнительно зависящую от числа частиц в системе: для системы из 10-ти частиц она имеет порядок 10⁴. Она обозначается буквойWи изменяется в диапазоне [1; +∞). Связь энтропии с термодинамической вероятностью установил Л. Больцман, представив ее в виде уравнения, названного его именем:

S=k*lnW , (13)

где k= R / N_А – константа Больцмана, равная 1,38*10^-23Дж/К.

Всякая изолированная система самопроизвольно стремиться принять состояние, характеризующееся максимальной термодинамической вероятностью– наиболее общая формулировка второго начала термодинамики.

На основании уравнения Больцмана можно показать, что любой необратимый процесс, самопроизвольно протекающий в изолированной системе, характеризуется увеличением энтропии. Рассмотрим процесс 1→2, смешение двух химически не взаимодействующих газов в условиях, представленных на рисунке. В состоянии 1 термодинамическая вероятность системы равна W₁. При удалении перегородки газы начнут самопроизвольно диффундировать друг в друга (смешиваться) до тех пор, пока молекулы каждого газа равномерно не распределятся по всему объему. В конечном состоянии 2 термодинамическая вероятность системы равна W_2. Система самопроизвольно перешла из менее вероятного состояния в более вероятное (W₂>W₁) при отсутствии энергетического обмена с окружающей средой. Единственной причиной протекания этого процесса является изменение энтропии:

ΔS=S₂-S₁=k*lnW₂- k*lnW₁= k*ln(W₂/W₁);

Но W₂>W₁, W₂/W₁> 1, ln(W₂/W₁)>0, следовательно, ΔS>0;

На этой основе сформулирован второй закон термодинамики для изолированных систем:

В изолированных системах самопроизвольно могут совершаться только такие необратимые процессы, в которых энтропия возрастает, т.е. ΔS>0.

Значение энтропии является мерой неупорядоченности процесса, зависит от агрегатного состояния, T, P и сложности системы, природы вещества. При прочих равных условиях:

S_г>S_ж>S_тв

Энтропия простых веществ зависит от их аллотропной формы:

S _{(Сграфит)} >S_{(Салмаз)} илиS (o₂) <S (o₃).

При повышении температуры энтропия возрастает:

если Т₁>T₂, тоS₁>S₂.

Энтропия системы при повышении давления уменьшается, так как снижается неупорядоченность движения частиц:

Если р₁>р₂ , тоS₁<S₂.

Энтропия системы при увеличении ее сложности повышается, т.к. вариантов расположения частиц становится больше.

Для энергетических характеристик вещества при стандартных условиях наряду со стандартной энтальпией Н⁰ используется стандартная энтропия S⁰вещества.

В отличие от стандартной энтальпии, стандартная энтропияпростых веществ не равна нулю. Энтропия всех веществ всегда больше нуля.

Все процессы, сопровождающиеся увеличением молекулярного беспорядка, в системе ведут к увеличению энтропии (ΔS>0):

- плавление и сублимация твердых веществ;

- испарение жидкостей;

-расширение газов;

- растворение кристаллов;

- химические реакции, сопровождающиеся увеличением количества вещества.

В процессах, связанных с затвердеванием жидкостей, кристаллизацией веществ из растворов, конденсацией паров и сжатием газов, степень молекулярного беспорядка уменьшается и энтропия системы убывает (∆S < 0).

Все перечисленные процессы мы обнаруживаем в разнообразных технологических цепочках, используемых при производстве композитов. Учет изменения энтропии системы в используемых процессах – необходимый элемент их научного обоснования.

Вычисление энтропии в различных процессах(обозначениеD_прS):

Пример 1. Фазовоепревращение чистого вещества.

При фазовых переходах первого рода энтропия и объем системы изменяются скачком, а температура остается постоянной (примеры: ). На практике эти переходы осуществляются обратимо в изобарно-изотермических условиях (p, T = const )по следующей схеме:

Фаза 1 ↔ Фаза 2; DН _пр=

Изменение энтропии при фазовых переходах первого рода вычисляют, интегрируя уравнение (4) при p, T = const (Q = Q_p):

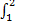dS= 1 / T 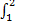dQ_р

D_прS = S₂ – S₁ = Q_p /T = DН_пр /T, (14)

где DН _пр, Дж/моль - это молярное изменение энтальпии (молярнаятеплота фазового перехода), Т – температура фазового перехода, К.

Пример 2. Изменение энтропии одного моля идеального газа в различных равновесных процессах:

Изменение энтропии одного моля идеального газа в различных равновесных процессах:

а) изохорный (V = const, dV = 0) нагрев от T₁ до T₂. Неравенство (9) для равновесного изохорного процесса превратится в уравнение

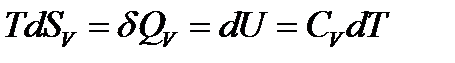
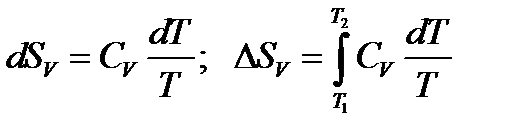
Если принять C_V = const в интервале температур T₁‑T₂, то

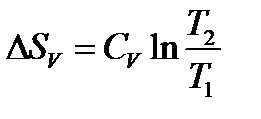(15)

б) изобарный (p = const) нагрев от T₁доT₂:

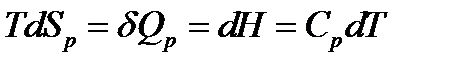
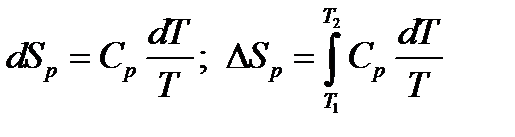
Принимая C_p = constв интервале температур T₁‑T₂, получаем

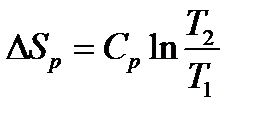(16)

Поскольку зависимости внутренней энергии U = C_VT (C_V = f(T)) и энтальпии H = C_pT (C_p = f(T)) от температуры справедливы для любого агрегатного состояния вещества, уравнения (15) и (16) можно использовать для расчета изменений энтропии в процессах изохорного и изобарного нагрева (и охлаждения) конденсированных веществ;

в) изотермическое (T = const) расширение объема от V₁ до V₂ (напомним, что для идеального газа при T = const, U = const, dU = 0):

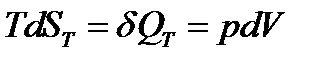
но для одного моля идеального газа 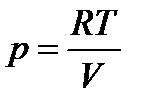, тогда

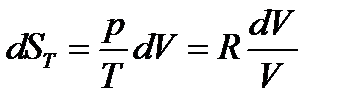
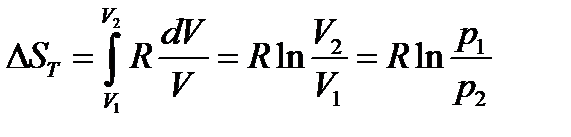(17)

так как, согласно закону Бойля – Мариотта, (pV)_T = const.

По формулам (14) – (17) вычисляются молярные изменения энтропий веществ в процессах (Дж/(моль·К)). Если количество вещества в системе равно n моль, то при умножении соответствующих молярных значений ΔS на n получают изменение энтропии системы в Дж/К.

Третий закон термодинамики

В отличие от абсолютных значений внутренней энергии (U) и энтальпии (Н), которые невозможно вычислить, абсолютные значения энтропии (S)поддаются определению как для сложных, так и для простых веществ из-за наличия у них начальной точки в шкале отсчета, установленной третьим законом термодинамики. Третье начало, называемое также постулатом Планка, звучит так: при температуре абсолютного нуля (Т=0К) энтропия идеальных кристаллов любого простого вещества или соединения равна нулю:limS_{Т → 0} = 0, или S₀ = 0.Предполагается, что в чистом, не имеющем дефектов кристалле вещества существует абсолютный порядок в расположении частиц , приТ = 0 К возможно единственное состояние системы, при котором частицы«застывают» в узлах кристаллической решетки, термодинамическая вероятность равна минимальному значению (W=1), поэтому для одного моля вещества S₀ = RlnW = Rln1 = 0.

Для неидеальных кристаллов, смесей, твердых растворов, стекол всегда S₀ >0, а W>1, т.е. у таких веществ существует так называемая нулевая энтропия, связанная с дефектами кристаллической решетки и др. причинами.

Стандартное значение энтропии обозначается символом S₂₉₈⁰, Дж/(моль· К). Стандартные значения энтропий S₂₉₈⁰различных веществ приводятся в таблицах термодинамических величин; это всегда положительная величина. Изменения энтропии в процессах (DS) могут быть положительными, отрицательными или равными нулю.

Схема расчета стандартных энтропий S₂₉₈⁰

Вблизи абсолютного нуля все вещества находятся в твердом состоянии. Если при стандартных термодинамических условиях вещество находится в кристаллическом состоянии, то в интервале температур 0 – 298 К энтропия изменяется только за счет повышения температуры, следовательно в соответствии с (16) при постоянном давлении

dS = dQ_р /T= dН / T = C_рdT /T,

или 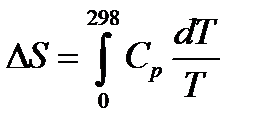,значит 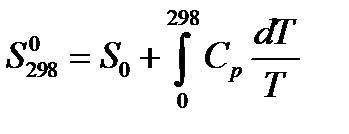, ноS₀ = 0в соответствии с третьим началом, таким образом,

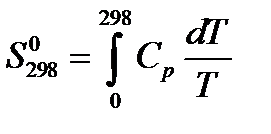
Если при Т =298 К вещество является газом, надо учесть изменения энтропии, связанные с фазовыми переходами (плавление, испарение):

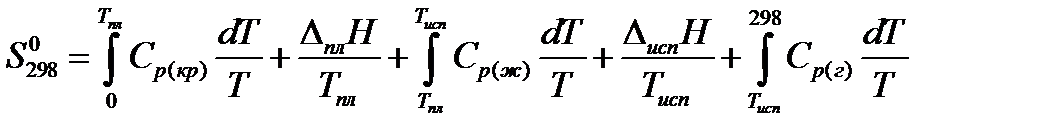(21)

Если при T = 298К вещество находится в жидком состоянии, при расчете стандартного значения энтропии в формуле (21) ограничиваются тремя первыми слагаемыми. Уравнение (21) является общим математическим выражением для расчета стандартных значений энтропий.

Так как энтропия является функцией состояния системы, то стандартное изменение энтропии в результате осуществления химической реакции (стандартная энтропия реакции) вычисляется как разность между суммой стандартных энтропий продуктов реакции и суммой стандартных энтропий исходных веществ с учетом стехиометрии процесса:

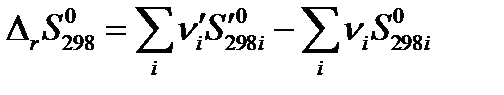(22)

т.е.

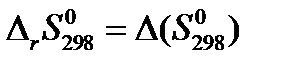(23)

где Δ в правой части уравнения (23) – знак оператора.

Лекция. Изменение энергии Гиббса и Гельмгольца – критерии направленности самопроизвольного процесса в закрытой системе

Реальные процессы проводятся, как правило, в закрытых системах в изобарно-изотермических (р, Т = соnst) или изохорно-изотермических (V, Т = соnst) условиях.

Для неизолированных систем нужно учитывать не только изменение энтропии, но и изменение энергии. Поэтому необходимо рассматривать две тенденции, определяющие направление самопроизвольно протекающих процессов:

1) стремление системы к достижению минимума энергии;

2) стремление системы к максимуму энтропии, т.е. к неупорядоченности.

Все процессы, при которых энергия в системе уменьшается, а энтропия возрастает, протекают самопроизвольно. Самопроизвольность других процессов зависит от того, какая из этих двух тенденций – энергетическая или энтропийная – окажется более эффективной, какая из этих противоборствующих тенденций получит перевес над другой. В этом проявляется противоречивость материального мира.

Для однозначной формулировки условия протекания самопроизвольных процессов в любых системах оказалось необходимым ввести еще две термодинамические функции, которые характеризовали бы одновременно и энергетику, и неупорядоченность данных систем. Впервые такую термодинамическую функцию ввел Д.У. Гиббс, и в память об этом выдающемся американском ученом ее назвали энергией Гиббса.

Критерием направленности самопроизвольного процесса в этих случаях является не знак изменения энтропии (ΔS), а знак изменения энергии Гиббса (ΔG) или энергии Гельмгольца (ΔF) в системе.

За энергию Гиббса (изобарно-изотермический потенциал) и энергию Гельмгольца (изохорно-изотермический потенциал) по рекомендации Международного союза теоретической и прикладной химии (IUPAC) принимаются следующие выражения: