Простые и сложные вещества

Для упрощения расчетов условно принято:

1) Стандартная разность энтальпий простых веществ в состоянии, устойчивом при стандартных условиях,принимается равнойнулю.

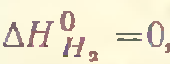
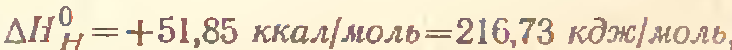
2) Стандартная разность энтальпий сложных веществ равна взятому с обратным знаком теплому эффекту образования моля данного соединения из простых веществ, взятых в состояниях, устойчивых при стандартных условиях.

Простые и сложные вещества при стандартных условиях:

-простые твердые

-простые жидкие

-простые газообразные

Наиболее т/д стабильная форма кристалла чистого вещества при стандартных условиях.

4 аллотропные модификации:

С-алмаз – нестабильный при стандартных условиях
-графит;

-фуллерен;

-графен.

Железо:

-Fe_α (т/д стабильно);

-Fe_β;

-Fe_γ;

-Fe_δ.

Простое жидкое вещество:

-Hg;

-Br.

Простое газообразное вещество:

H₂, O₂, Cl₂…

Сложным называется вещество, которое можно гипотетически или реально синтезировать из соответствувющих количеств простых веществ в стандартных термодинамических условиях.

В этом случае тепловой эффект образования сложного вещества:

С_{(графит)}+О_2(г) ->CO_2(г)Δ_р H⁰₂₉₈=-393.5 кДж (1)

С_{(графит)}+Н_2(г) ->CO_2(г) Δ_р H⁰₂₉₈=-49 кДж (2)

2К+2Cr+3.5O₂->K₂Cr₂O₇ Δ_р H⁰₂₉₈=-2067 кДж (3)

Тепловые эффекты (1)-(3) являются стандартным изменением энтальпий реакций. А форма записи уравнений т/д формой.

С_{(алмаз)+}О₂->CO_{2(г) )}Δ_р H⁰₂₉₈=-393.5 кДж (4)

СО(г)+0,5О₂->СО_{2(г) )}Δ_р H⁰₂₉₈=-283.5 кДж (5)

Изменение энтальпии в реакциях (4)-(5) не является реакциями образования диоксида углерода. Так как в (4) случае не находятся в стандартном состоянии, а в (5) сложное вещество-одно из исходных веществ не является простым веществом.

Гипотетически продукт может находиться в разных фазовых состояниях.

Образование воды: H_2(г)+0,5О_2(г)->Н₂О_(ж)Δ_р H⁰₂₉₈=-285,8кДж (6)

Образование пара: H_2(г)+0,5О_2(г)->Н₂О_(г)Δ_р H⁰₂₉₈=-241,8кДж (7)

Энтальпию реакции обозначают ∆Н_р, стандартную энтальпию реакции обозначают ∆Н⁰_р , кДж/моль. Иногда используется индексы f(от англ. formation - образование) и с(от англ. сombustion - горение).

По определению стандартная энтальпия образования любого простого вещества в т/д стабильном состоянии равно 0 при любой температуре.

Δ _fH⁰_T=0;

Термохимия и термохимические расчеты.

Существуют следующие законы термохимии:

1 закон термохимии - закон Лавуазье-Лапласа:

Тепловой эффект реакции разложения какого-либо вещества в точности равен и обратен по знаку тепловому эффекту образования этого вещества.

(Следствие 1 закона термодинамики)

2 закон термохимии - закон Гесса.

Тепловой эффект данной химической реакции не зависит от характера и от последовательности отдельных ее стадий, а зависит от начальных и конечных веществ и их физического состояния.

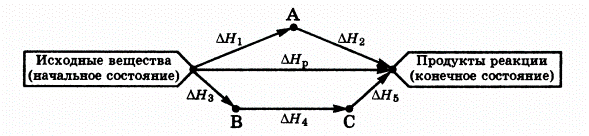
Энтальпия реакции зависит только от природы и состояния исходных веществ конечных продуктов и не зависит от пути, по которому протекает реакция.

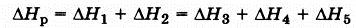
Закон Гесса позволяет рассчитывать тепловые эффекты химических реакций, которые невозможно или трудно определить экспериментально.

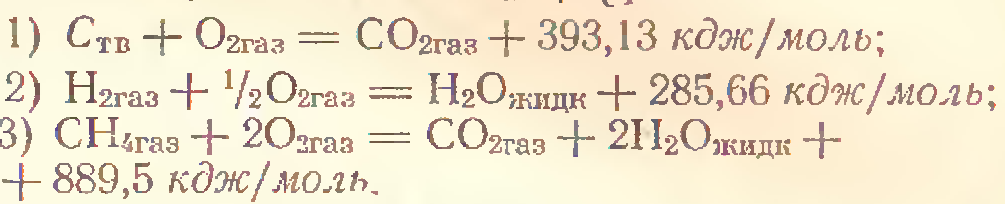
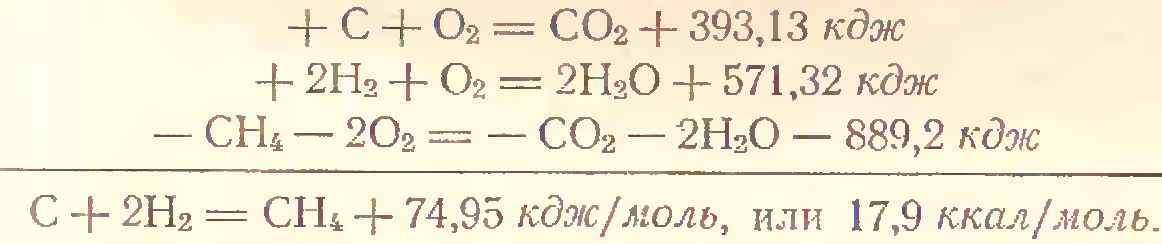
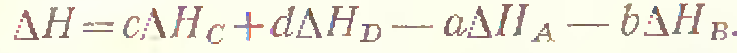
Если задача решается при температуре Т, отличной от стандартной, то при вычислении посл. суммы, то значение энтальпий должно быть представлено в следующей форме:

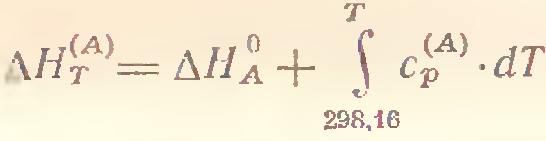
Закон Гесса широко используются для расчета энтальпий веществ, определить которые непосредственным экспериментом невозможно.

Энергетические расчеты, связанные с химическими реакциями, в настоящее время ведутся с использованием справочных данных по значениям стандартных разностей и их зависимостей от температуры (теплоемкости, теплоты превращений).

Порядок расчета разности энтальпий химической реакции рассмотрим на примере обобщенного процесса:

,

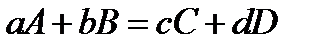гдеA, B, C, D – символы веществ;

a, b, c, d – коэффициенты уравнений реакций.

Разность энтальпий системы, в которой произошла реакция, определяется по выражению

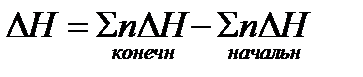
где ΔH – разность энтальпий системы в результате прошедшей химической реакции (для сокращения будем называть ее просто разностью энтальпий реакции; разности энтальпий продуктов реакции будем называть энтальпии);

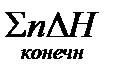‑ сумма энтальпий продуктов в конечной системе, равная ;

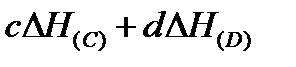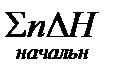‑ сумма энтальпий веществ в начальной системе, равная .

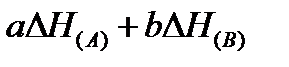Следовательно,

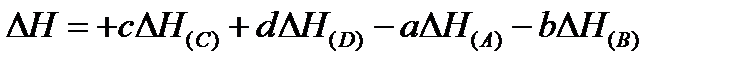
Практически справочные данные по разностям энтальпий подписывают прямо под уравнением химической реакции, соблюдая соответствующие знаки:

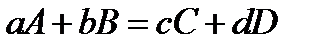
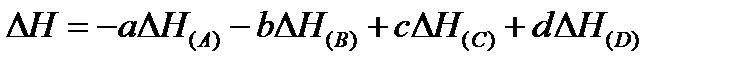
Если задача решается при стандартных условиях, то разности энтальпий имеют нуль сверху ( 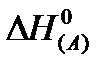), если при других температурах, то вводят индекс T внизу, а индекс вещества переводят вверх ( ).

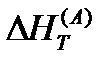Зависимости разности энтальпий реакции от температуры можно найти легко, зная зависимости от температуры энтальпий отдельных веществ.

Рассмотрим в качестве примера принятый ранее обобщенный процесс, полагая для простоты, что все вещества находятся в газообразном состоянии:

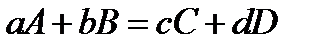
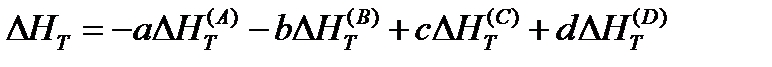
Значение энтальпий каждого вещества может быть представлено уравнением вида:

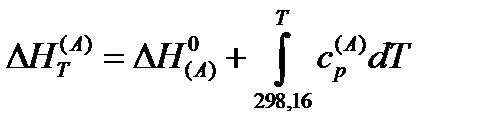
Подставляя значения энтальпий отдельных веществ в предыдущие выражения, получаем:

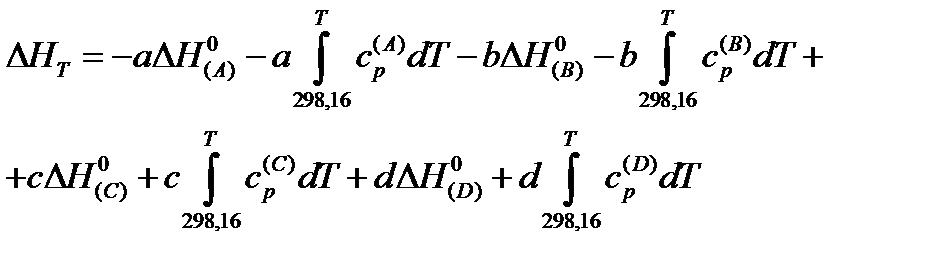
Члены выражения, не содержащие интегралов, группируясь, дадут разность энтальпий химической реакции при стандартных условиях 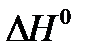, а члены, содержащие интегралы, можно объединить общим выражением:

,

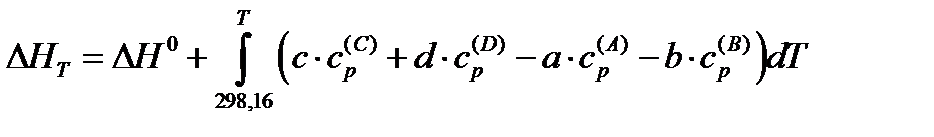или

,

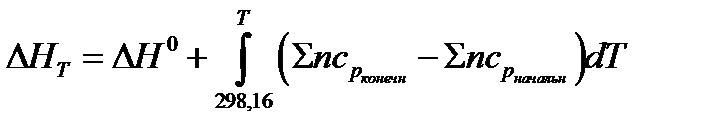или можно условно записать еще короче:

.

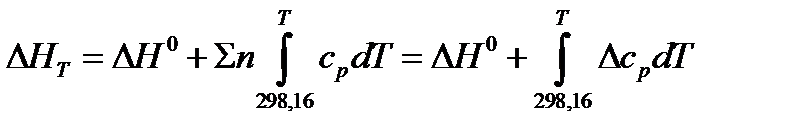В последнем случае нужно помнить, каким образом суммируются интегралы для начальных и конечных веществ. Значения уже взятых интегралов 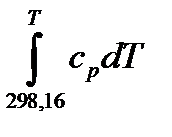можно для некоторых веществ и различных значений T найти в таблицах.

Так как разность энтальпий реакции находится через интегралы в пределах, то, для обобщения задачи, можно, подставив уравнения зависимости теплоемкости от температуры, преобразовать решение и получить его в виде непрерывной температурной функции, удобной для исследования.

При практических расчетах применяют различные степени приближения:

1) пренебрегают температурной зависимостью теплового эффекта реакции по уравнению Киргхофа и считают

Δ_rН_T⁰ ~ Δ_rН₂₉₈⁰= const;

или

2) принимают для рассматриваемой реакции

Δс_р ~Δс_р⁰₂₉₈= const

ВеличинаΔс_р⁰₂₉₈вычисляется по стандартным значениям теплоемкостей.

Формула Киргофа:

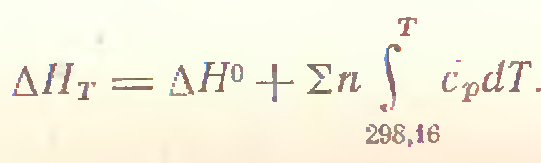[1]

Продолжение

Первый закон термодинамики не дает ответа на вопрос, в каком направлении пойдет исследуемый процесс, пойдет ли он вообще и как полно завершится. Для описания движения материи при протекании процессов в системе необходимо знать энергию и энтропию частиц системы. Энергия и энтропия -две функции состояния системы, характеризующие движение частиц, образующих систему. К этим двум величинам часто в современных моделях добавляется третья - информация.

Энтропия (S)- термодинамическая функция, характеризующая меру неупорядоченности системы, т.е. неоднородности расположения и движения ее частиц. Изменение энтропии системы выступает в качестве меры необратимости в любом процессе, протекающем в ТС.

Конструируя композиты, мы стемимся внести в систему определенную упорядоченность.

Информация (I) - мераорганизованности системы, т.е. упорядоченности расположения и движения ее частиц.

В самоорганизующихся системах действует закон сохранения:

I + S = const

Физический смысл этого закона: за полученную информацию система платит уменьшением своей энтропии. Как следствие, появился термин «структурно-информационные свойства систем».