Применение теоремы Остроградского - Гаусса для расчета электростатического поля бесконечного заряженного цилиндра

Пусть бесконечный цилиндр радиуса R равномерно заряжен с линейной плотностью заряда t > 0, что соответствует положительно заряженному цилиндру. Силовые линии электрического поля направлены в любой точке вне цилиндра по радиальным линиям (рис. 12.4). Найдем напряженность поля вне цилиндра, на расстоянии r > R от его оси. Проведем вспомогательную цилиндрическую поверхность 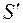длиной l и радиусом r, которая охватывает цилиндрический проводник. В любой точке поверхности 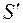вектор Eнаправлен вдоль вектора 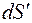. Рассмотрим элемент проводника длиной dl. Заряд, заключенный на поверхности элементарного цилиндра радиуса R:

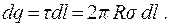(12.15)

Найдем поток вектора Eчерез боковую поверхность вспомогательного цилиндра S':

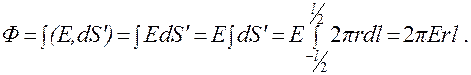(12.16)

Согласно теореме Остроградского - Гаусса

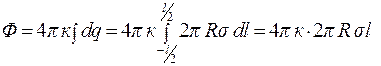(12.17)

следовательно 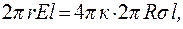отсюда находим напряженность электрического поля вне цилиндра:

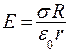(12.18)

Выразим напряженность поля через линейную плотность заряда t:

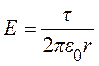(12.19)

Внутри цилиндра напряженность поля E = 0, т.к. заряды равномерно распределяются по поверхности. Вне цилиндра напряженность электрического поля изменяется обратно пропорционально r и совпадает по величине с напряженностью поля бесконечной заряженной нити, расположенной вдоль оси цилиндра.

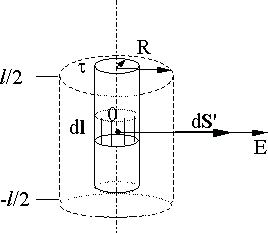
Рис. 12.4.

ГЛАВА 13. РАБОТА ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПОТЕНЦИАЛ.