Потенциал заряженной сферы, плоскости, цилиндра

Найдем потенциал, создаваемый проводящей заряженной сферой радиуса R. Как известно, внутри сферы (при r < R) E = 0; вне сферы (при r > R) 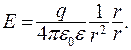С учетом формулы (13.18), связывающей напряженность и потенциал, находим:

1. 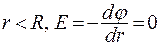, отсюда j = const;

2. 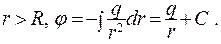(13.21)

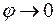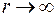Постоянную C выберем из условия, что при , отсюда C = 0. Потенциал внутри проводящей сферы имеет одинаковое значение во всех точках внутри сферы и равен потенциалу на поверхности:

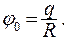(13.22)

Потенциал вне заряженной сферы равен потенциалу точечного заряда, помещенного в центр сферы.

На рис. 13.6 приведен график зависимости потенциала j от расстояния до центра сферы r.

Для проводящего шара получим тот же результат, что и для сферы.

Найдем теперь потенциал заряженной бесконечной плоскости с поверхностной плотностью заряда s (рис. 13.7).

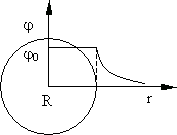
Рис. 13.6.

Напряженность электрического поля плоскости: 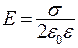. Потенциал j получим в виде

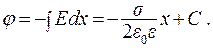(13.23)

Выберем начало отсчета потенциала так, чтобы при x = 0, потенциал был равен 0, тогда C = 0.

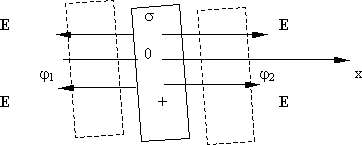
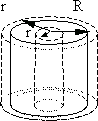
Рис. 13.7. Рис. 13.8.

Потенциал электрического поля заряженной плоскости:

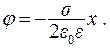(13.24)

Разность потенциалов между двумя точками поля

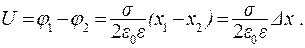(13.25)

Потенциал электрического поля заряженного цилиндра:

Потенциал заряженного бесконечного цилиндра с линейной плотностью t найдем из соотношения:

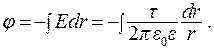(13.26)

Потенциал поля внутри цилиндра (рис. 13.8) является постоянной величиной при r < R и равен потенциалу на поверхности цилиндра, т.к. E = 0 внутри цилиндра. Потенциал вне заряженного цилиндра (r > R): 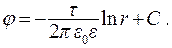Если принять, что потенциал j на поверхности цилиндра (при r = R) равен нулю, тогда постоянная 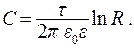Потенциал вне цилиндра имеет такую же величину, как и потенциал заряженной нити, помещенной на оси цилиндра

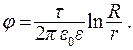(13.27)