Применение теоремы Остроградского - Гаусса для расчета электростатического поля бесконечной заряженной плоскости

Найдем напряженность электрического поля бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда s. Пусть s > 0, т.е. плоскость заряжена положительно. Силовые линии напряженности электрического поля направлены симметрично в обе стороны от плоскости, перпендикулярно к ней (рис. 12.3). Проведем замкнутую цилиндрическую поверхность перпендикулярную плоскости так, чтобы цилиндр вырезал круг площадью S. Основания цилиндра параллельны плоскости и имеют площадь S. В любой точке основания цилиндра вектор dS направлен перпендикулярно к основанию и совпадает по направлению с вектором E. В любой точке боковой поверхности вектор dS перпендикулярен к вектору E. Полный поток через замкнутую поверхность состоит из потока 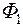через два основания и потока через боковую поверхность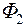

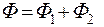(12.12)

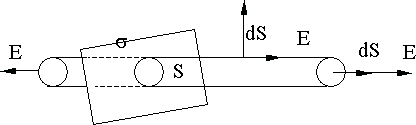
Рис. 12.3.

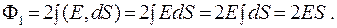(12.13)

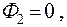Поток через боковую поверхность т.к. вектор E перпендикулярен вектору dS, поэтому полный поток Ф_E = Ф₁ = 2ES. Из теоремы Остроградского - Гаусса находим: 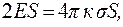поскольку заряд на поверхности S, вырезанной цилиндром: 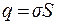. Найдем напряженность бесконечной плоскости:

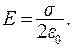(12.14)

Поле бесконечной заряженной плоскости является однородным, оно одинаково во всех точках пространства и не зависит от расстояния до плоскости.