Применение теоремы Остроградского - Гаусса для расчета электростатического поля равномерно заряженного сферического проводника

Найдем поле сферического проводника радиуса R, на поверхности которого распределен заряд q > 0. Для того чтобы найти напряженность электрического поля E в любой точке на расстоянии r > R от центра, проведем вспомогательную сферическую поверхность радиуса r (рис. 12.1).

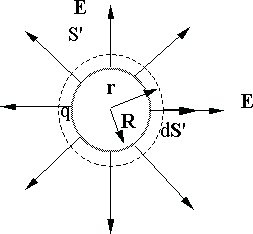
Рис. 12.1.

Найдем поток вектора E через сферу поверхностью 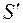. Вектор 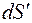в любой точке сферической поверхности направлен по внешней нормали к этой поверхности, его направление совпадает с направлением вектора E в любой точке поверхности сферы.

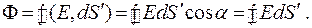(12.9)

Вследствие симметрии модуль вектора E имеет постоянное значение во всех точках вспомогательной поверхности, поэтому можно вынести E из-под знака интеграла:

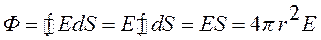(12.10)

Из теоремы Остроградского - Гаусса следует, что 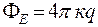, таким образом находим 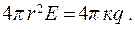Отсюда следует, что напряженность электрического поля вне сферического проводника:

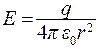(12.11)

Напряженность электрического поля в любой точке внутри сферы найдем, проведя вспомогательную сферическую поверхность S' радиусом r < R. Поскольку заряд q распределен по поверхности, то внутри проводника 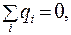следовательно,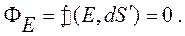

Отсюда следует, что внутри сферы E = 0

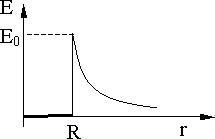
Рис. 12.2.

На рис. 12.2 представлен график зависимости напряженности электрического поля E сферического проводника от расстояния r до центра сферы. Напряженность электрического поля скачком изменяется на границе сферы от E = 0 до 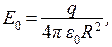и спадает пропорционально 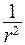вне сферы. Напряженность заряженного шара совпадает с напряженностью сферического проводника, т.е. в проводнике заряд переходит на поверхность и равномерно распределяется по ней. Напряженность поля вне сферического проводника имеет такой же вид, как и напряженность точечного заряда q, помещенного в центр сферы.