Электрический потенциал

Потенциал j определяется как электрическая потенциальная энергия единичного положительного заряда, помещенного в данную точку поля:

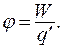(13.13)

Потенциал поля, создаваемого зарядом q, не зависит от величины пробного заряда q', помещенного в это поле:

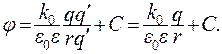(13.14)

Потенциал, также, как и энергия, определяется неоднозначно и зависит от выбора постоянной C.

Электрический потенциал численно равен работе, которую необходимо совершить, чтобы перенести единичный заряд q' из бесконечности на расстояние r от точечного заряда q.

Пусть при 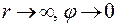, тогда положим С = 0.

Потенциал точечного заряда будет иметь вид:

(13.15)

На рис. 13.2 показана зависимость потенциала точечного заряда j от расстояния r до заряда. Единица измерения потенциала

Вольт, [j] = В, 1В = 1Дж/1Кл.

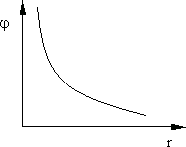
Рис. 13.2.

Напряжением U называется разность потенциалов между двумя точками, численно равная работе, которую необходимо затратить для перемещения единичного заряда из точки 1 в точку 2:

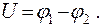(13.16)

Единица измерения напряжения – Вольт, [U] = В.

Вольта Алессандро (1745 – 1827), итальянский физик, химик и физиолог, родился в Комо. Учился в школе ордена иезуитов. Сконструировал первый источник электрического тока – вольтов столб. Открыл взаимную электризацию разнородных металлов при их контакте. Построил электроскоп, конденсатор.

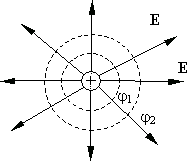
Рис. 13.3.

Если каждой точке поля сопоставить вектор напряженности E, то получим векторное поле, если же в каждой точке пространства задать определенное число j, то образуется скалярное поле. В скалярном поле можно провести поверхности, которые называются эквипотенциальными. В каждой точке эквипотенциальной поверхности потенциал имеет постоянную величину, j = const. Поверхности эти проводят так, чтобы разность потенциалов на соседних поверхностях составляла: .

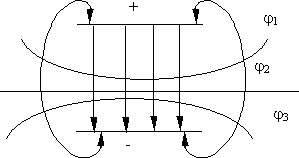
Рис. 13.4.

На рис. 13.3 изображены силовые линии положительного точечного заряда и перпендикулярные к ним эквипотенциальные сферические поверхности с потенциалами 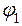, 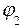. На рис. 13.4 изображены силовые линии и эквипотенциальные поверхности электрического поля, создаваемого двумя разноименно заряженными плоскостями.

Поверхность заряженного проводника имеет одинаковый потенциал во всех его точках, поэтому эквипотенциальные поверхности повторяют форму проводника (рис. 13.5).

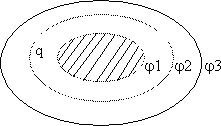
Рис. 13.5.

Потенциал j изменяется от точки к точке пространства. Это изменение можно характеризовать с помощью векторной величины, называемой градиентом потенциала. В декартовой системе координат

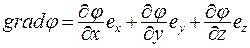
где - частные производные от потенциала по координатам x, y, z;

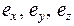- единичные векторы вдоль осей координат х, y, z.

Если потенциал зависит только от одной координаты, например, от радиуса r, тогда

Зная распределение потенциала в пространстве, можно определить напряженность электрического поля:

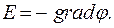(13.18)

В случае однородного поля напряженность связана с напряжением соотношением:

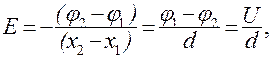(13.19)

где U – напряжение;

d - расстояние между двумя точками в пространстве.

Электрическое поле между обкладками плоского конденсатора является однородным, также как и поле в проводниках. Если напряженность зависит только от одной координаты x , то связь между напряженностью и потенциалом имеет вид:

(13.20)

Знак минус в формуле указывает, что электрическое поле направлено в сторону уменьшения потенциала.