Теорема Остроградского-Гаусса для электростатического поля в вакууме

Потоком вектора напряженности электрическогополя Ечерез малый участок поверхности площадью dS называется скалярное произведение вектора напряженностина вектор dS:

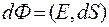(12.1)

где Е– вектор напряженности электрического поля;

dS=dSn –вектор, направленный по нормали n к площадке dS.

Поток вектора Е через поверхность S:

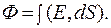(12.2)

Найдем поток вектора напряженности электрического поля, создаваемого системой точечных зарядов 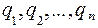, через замкнутую поверхность:

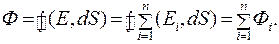(12.3)

Полный поток равен алгебраической сумме потоков, создаваемых отдельными зарядами.

В случае непрерывного распределения заряда по поверхности тела принцип суперпозиции не позволяет определить напряженность электрического поля, создаваемого телом. Одним из методов решения задач электростатики является применение теоремы Остроградского - Гаусса.

Поток вектора напряженности электрического поля через любую замкнутую поверхность численно равен алгебраической сумме зарядов, находящихся внутри этой поверхности, умноженной на 4pk.

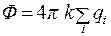(12.4)

где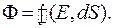

Теорему Остроградского – Гаусса запишем в интегральной форме:

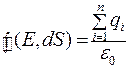(12.5)

Применяя теорему Остроградского – Гаусса, можно рассчитать поле, создаваемое заряженными телами произвольной формы. Если заряды непрерывно распределены по объему, то теорему Остроградского - Гаусса можно написать в виде

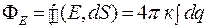(12.6)

или в виде

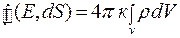(12.7)

где r - объемная плотность заряда.

В дифференциальной форме теорема Остроградского – Гаусса:

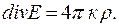(12.8)

Остроградский Михаил Васильевич (1801 – 1862), отечественный математик и механик, родился в Пашеновке Полтавской обл. Учился в Харьковском ун-те.

Известны его работы в области математического анализа, математической физики, теоретической механики. Решил ряд задач гидродинамики, теории теплоты, упругости, баллистики. В 1828 г. доказал теорему о преобразовании интегралов.

Гаусс Карл Фридрих (1777 – 1855), немецкий математик, астроном и физик, родился в Брауншвейге. Учился в Геттингенском ун-те. Работы посвящены теории поля, электростатике, магнетизму.