Особенности силового анализа ременных передач

Исходными данными для силового анализа ременных передач, как и передач зацеплением, является номинальная нагрузка (T₁, T₂) и геометрические параметры (d₁; d₂; α₁ и т.п.). В задачу данного расчета входит определение сил, действующих на элементы передачи и в первую очередь на ее очевидный слабый элемент - ремень. В ремне, как констатировано при обсуждении принципа работы передачи, выделяют окружную силу F_t, силы натяжения ремня - предварительного F_o, набегающей F₁ и сбегающей F₂ ветвей. Кроме того на массу ремня, совершающую криволинейное движение при огибании шкивов, действует центробежная сила, вызывающая соответствующие натяжения ремня F_ц. В силовом расчете также устанавливают нагрузку на валы, опоры и корпусные детали.

Силовой анализ ременной передачи, как и вообще первичный силовой расчет механизмов, выполняется для установившегося движения, и основу расчетных моделей составляют условия равновесия элементов передач. Величина окружной силы может быть установлена из равновесия ведущего шкива под действием движущего момента T₁ и момента сил трения шкива о ремень, препятствующего его движению, а ведомого - моментов сил трения и сопротивления Т_2(С) (рис.10.3б)

; ;

; .

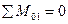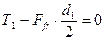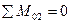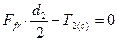Учитывая, что F_t = F_fr можно записать

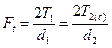. (10.12)

Условия равновесия ремня на шкивах ( 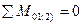) позволяют установить зависимость между F_t, F₁ и F₂. В соответствии с рис.10.3б это условие имеет следующий вид

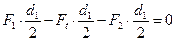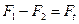или . (10.13)

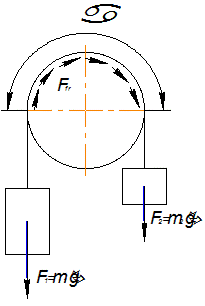Рис.10.9. К оценке силы тре ния между цилиндрической поверхностью и гибкой не- весомой нитью.

Соотношение между натяжением ремня в ненагруженном и нагруженном моментом T₁ состо-

яниях устанавливает зависимость Понселе:

F₁+F₂=2F₀ . (10.14) . Левая часть уравнения (10.14) является суммарным натяжением ветвей ремня в нагруженном состоянии, а правая – суммарным натяжением ветвей при T₁= Т_{2( С)} = 0.

Поскольку расстояние между шкивами, а, следова- тельно, и суммарная деформация ремня в обоих состояниях не изменяется, то в соответствии с за- коном Гука между ними поставлен знак равенства.

Система уравнений (10.13 - 10.14) содержит три неизвестных (F_o, F₁ и F₂) и не замк-нутой. В качестве замыкающего уравнения при анализе дополнительно используют формулу Эйлера: 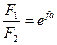, (10.14)

где е - основание натурального логарифма; f – ко- эффициент трения: α - угол обхвата. Зависимость (10.15) устанавливает предельное соотношение между натяжениями ветвей гибкой невесомой нити, при которых разность сил тяжести грузиков уравновешивается на цилиндре силой трения (рис 10.9). Как отмечалось выше, правомерность использования зависимостей классической механики в расчете реальных элементов машин требует установление адекватности условий их работы и тех условий, для которых зависимости получены. В этой связи следует заметить, что ремень в отличие от гибкой невесомой нити обладает массой и жесткостью. Наличие массы ремня в случае его движения по криволинейной траектории при огибании шкивов приводит к возникновению центробежной силы F_ин, которая оттягивает ремень от шкива, естественно снижая силу трения, т.е. изменяет параметр, оцениваемый формулой Эйлера. Жесткость ремня существенно влияет на угол обхвата, входящий в показатель степени (10.15) и также существенно определяет силу трения. Таким образом, условия получения зависимости (10.15) не соответствует условиям работы ременной передачи. Однако формула Эйлера успешно применяется для их силового расчета. При этом влияние центробежной сила учитывается в дальнейших расчетах, а в качестве угла обхвата используют угол скольжения α = α_ск, определяемый с учетом жесткости ремня. Зависимость (10.15) с учетом (10.13) можно записать так

,

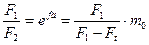где т₀ =e^fa. Из этой зависимости максимальное натяжение ремня можно выразить через

практически задаваемую силу F_t

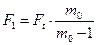. (10.16)

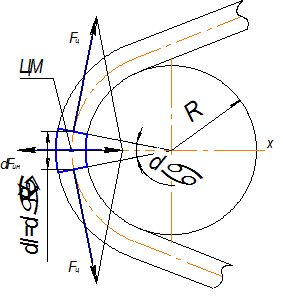
Рис.10.9. К оценке силы ремня центробежной силой.

Расчетная схема для оценки силы натяжения от центробежной силы показана на рис.10.10. Если вырезать на угле обхвата углом dα элементарный участок ремня массой dm движущийся со скоростью υ, то он будет находиться в равновесии под действием инерционной силы dF_ин и натяжений ремня F_u, инерциируемых этой силой. В качестве уравнения равновесия очевидно использова- ние суммы проекций на ось X (∑X=0) 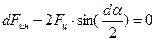. (10.16).Учитывая, что 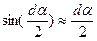, а центробежная сила dF_ин = dm × υ² / R (R- радиус траектории центра масс (ЦМ) выделенного участка), можно записать

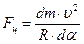
За радиус траектории R без заметной погрешности расчетов принимают радиус шкива (R = d / 2), а массу участка ремня вычисляют по произведению длины участка dl = da× R и погонной массы ремня (массы единицы длины) q, приводимой для серийных ремней в справочных таблицах. После подстановки указанных параметров в (10.16) окончательно получаем

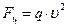. (10.17)

Нагрузка на валы, опоры и корпусные детали в ременной передаче прежде всего обусловливается силами натяжения ремня. Для оценки этой нагрузки необходимо, при-

вести силы F₁ и F₂ к валу, используя правило параллель­ного переноса сил (рис.10.11). В случае расчета тихоходных передач (υ<(1 - 2)m/c) центро­бежную силу можно во внима­ние не принимать. Тогда, оче­видно из рис.10.11 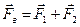,а модуль этой силы

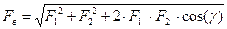. (10.18)

В быстроходных передачах необходимо учитывать, что центробежная сила оттягивает ремень от шкива и уменьшает нагрузку валов

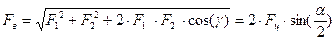. (10.19)

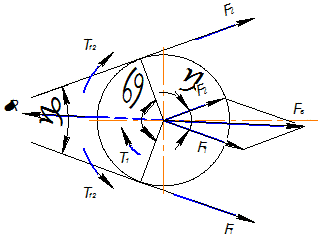
Рис.10.11. Расчётная схема определения нагрузки на валы в ременных передачах.

на расчетной схеме и в зависимостях (10.17 - 10.19), γ- угол между ветвями ремня, α - угол обхвата. Как следует из рис.10.11, вектор F_в несколько отклоняется от линии, соединяющей оси шкивов в сторону большего вектора F₁, однако при расчете валов и осей без большой погрешности его можно направлять по этой линии. Нагрузка на вал F_в уравновешивается суммарной реакцией опор ∑R, показанной на расчетной схеме пунктиром, которая далее нагружает опоры, корпусные и крепежные детали.

Практическое занятие №3.

Информационные материалы к курсовому проектированию

”Выбор материалов зубчатых колес и определение допускаемых напряжений”

Цель занятия - закрепление методики расчетов ДМ на прочность в части определения допускаемых напряжений на примере частной задачи проектирования зубчатых передач.

Задачи занятия:

1. знакомство с материалами и их термической, химико – термической обработкой, используемых в машиностроении для производства деталей зубчатых механизмов, и особенностями назначения материалов для шестерен и зубчатых колес;

2. освоение методов определения допускаемых напряжений при расчётах ЗП на контактную, изгибную выносливость и квазистатическую прочность контактную и изгибную; знакомство с алгоритмом обсуждаемого этапа проектирования ЗП.

1. Материалы зубчатых колёс и их термическая и химико-термическая обработки

Для производства зубчатых колёс используют разнообразные стали, чугуны и пластмассы. В машиностроении главным образом применяются стальные ЗК. Стали для производства ЗК принято разделять на три группы.

К первой группе относят стали, обеспечивающие при соответствующей термической или иной обработке твердость рабочих поверхностей зубьев шестерен и колес Н_1,2 > 350НВ и имеющие неоднородную структуру материала в зоне зубьев. Эта группа обладает наиболее высокими прочностными свойствами, обеспечивающих минимальные размеры и стоимость передач и узлов, в состав которых они входят. Высокая твёрдость поверхностей зубьев практически исключает возможность их формообразование после получения требуемой твёрдости. Термическая или иная обработка после нарезки зубьев приводит к их короблению, что обусловливает необходимость дополнительной обработки с целью получения требуемой точности зацепления. Дополнительная обработка усложняет технологию изготовления ЗК однако их большая нагрузочная способность и меньшая стоимость делают эту группу наиболее перспективной и распространенной. Существует устойчивая тенденция к расширению использования этой группы сталей при мощности Р>(1,5…2) кВт. Ограничение в применении зубьев с твердостью Н>350 НВ касается лишь передач малой мощности P<(1.5…2) кВт, в которых их использование

приводит к получению малых межосевых расстояний, что усложняет условия обеспечения работоспособности валов и опор. Кроме того усложнение технологии изготовления ЗК таких передач не компенсируется снижением их размеров, массы и стоимости.

При выборе марок стали этой группы для шестерни и колес обычно стремятся к максимальному удовлетворению условию равнопрочности их зубьев. Известно, что с позиции условий работы в более сложных условиях находятся зубья шестерен, получающие большее число циклов напряжений N_∑, а так же зубья промежуточных колес, в которых изгибные напряжения изменяются по знакопеременному циклу. По этой причине для них целесообразно назначить материал, обладающий повышенными прочностными свойствами. Однако на этапе проектных расчетов, какое либо осознанное решение принять практически невозможно. По этой причине продуктивнее при проектных расчётах принять одинаковые марки сталей, корректируя их на этапе проверочных расчетов. На стадии проектных изысканий можно также опираться на накопленный опыт в сочетании марок сталей и их термической и других обработок, работающих в условиях, аналогичных проектируемым объектам. Эффективно также опираться на опыт производителей, которые планируют изготовление проектируемых передач.

Ко второй группе относят стали с термическими обработками, обеспечивающими однородную структуру сплава по всему объему зубчатого колеса с твёрдостью Н_1,2<=350НВ. Подобное достигается с помощью отжига, нормализации или улучшения. Прочностные параметры материала шестерен, промежуточных колес по приведенным ранее соображениям берутся более высокой твердости поверхности их зубьев

НВ_1,пр= НВ₂ + (20 … 40)НВ,

где НВ_1(пр)=(НВ_{1,(пр)мах} + НВ_1,(пр)min )* 0,5 – расчетная средняя твердость зубьев шестерен (промежуточных колес);

НВ₂ – расчетная средняя твердость зубьев колеса.

Формообразование зубьев и их окончательная обработка при твёрдости H<350HB, производится после названной термической обработки. Это обстоятельство упрощает и удешевляет технологию изготовления зубчатых колес. ЗК обсуждаемой группы сталей обладают хорошей прирабатываемостью и потому менее требовательны к точности изготовления передачи и жесткости валов. Однако эти достоинства второй группы сталей не компенсируют их низкую нагрузочную способность, высокую материалоемкость и стоимость. В соответствии с последним использование сталей второй группы целесообразно главным образом при малых передаваемых мощностях – Р<=(1,5 … 3)кВт.

В третьей комбинированной группе сталей для шестерен, а также промежуточных колес, сателлитов, выбирают материалы, термическую и иную обработку такими, которые обеспечивают твердость активных поверхностей зубьев Н_1(пр) >350НВ, а для колес – Н₂<=350НВ. Такое сочетание твердостей существенно упрощает технологию нарезки зубьев значительных по размерам зубчатых колёс (формообразования зубьев, как и в сталях второй группы, производиться после термической обработки). Кроме того в обсуждаемом случае значительно активнее происходит процесс приработки зубьев и контактное выкрашивание не носит прогрессирующего характера. Особенно эффективно приработка происходит в косозубых зубчатых колесах. При использовании сталей третьей группы обычно рекомендуют принимать разницу в твердости рабочих поверхностей зубьев шестерни и колес до 70НВ

НВ₁=НВ₂+70НВ.