Формирование расчетной модели
Работоспособность по критерию контактной выносливости рабочих поверхностей зубьев будет обеспечена при выполнении условия σн ≤ [σн].
1.1.2.1. В основе расчетной модели определения допускаемых напряжений лежит универсальная зависимость(1.6)
[σ] = 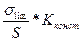 .
.
а) Предельные напряжения σlim как известно зависят от параметров ФМС материалов, характера нагрузки, суммарного числа циклов напряжений в случае циклической нагрузки и конструктивных факторов. Поскольку материалы зубчатых колес, их термическая и другие обработки, параметры физико-механических свойств в проверочном расчете известны, а также очевидным является циклическая нагрузка знакопостоянного пульсирующего цикла на активные поверхности зубьев (по аналогии с поверхностью фрикционных катков, рассмотренных в лекции №3), то в качестве σlim следует принять предел выносливости при указанном цикле и соответствующем суммарном числе циклов напряжений. Суммарное число циклов контактных напряжений, физически равное количеству контактов сопряженных поверхностей за весь период эксплуатации, определяется по очевидной зависимости:
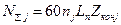 , (2.10)
, (2.10)
где nj – частота вращения j элемента передачи – шестерни n1, колеса n2, промежуточного (паразитного) колеса nпр (рис 2.8),
Zконj – число контактов зуба j элемента одной его стороной.
Методика оценки последнего параметра очевидна из рассмотрения рис.2.8. В однопоточной передаче (рис.2.1,а) число контактов для шестерни и колеса Zкон1= Zкон2=1, а для двухпоточной (с приводом от одной шестерни двух колёс (рис 2.8б)) – Zкон1=2, Zкон2 =1. Характерно, что для зубьев передачи с паразитным (промежуточным) колесом (рис 2.8в) Zкон1= Zкон2 = Zкон3=1. Zкон3=1 в силу того, что зубья паразитного колеса контактируют с шестерней одной стороной зуба, а с колесом − противоположной.
а) б) в)
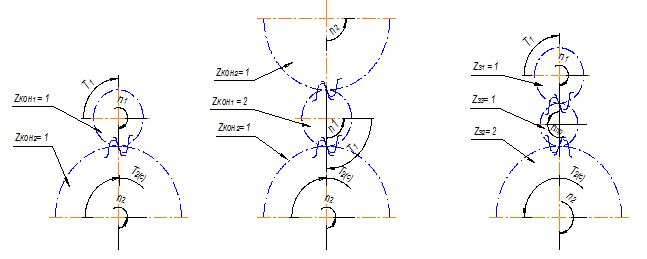
Рис 2.8. Определение числа контактов Zконj одной стороны зуба за один оборот для зубчатых механизмов: а) однопоточного, б) двухпоточного, в) с промежуточным (паразитным) колесом
Поскольку предельные напряжения зависят от суммарного числа циклов напряжений, их следует определять для всех элементов передачи (шестерни, колеса, промежуточного колеса при наличии последнего). Значения σlim во второй и третьей зонах кривой усталости с учетом ограничений коэффициента долговечности можно определять по универсальной зависимости (1.13)
σlimj = σ0j КLj = σoHlimb KHLj . (2.11)
σoHlimb – международное обозначение длительного предела контактной выносливости при знакопостоянном пульсирующем цикле, величина которого зависит, главным образом, от твердости рабочих поверхностей зубьев. Например, для нормализованных и улучшенных зубчатых колес − σoHlimb = 1.8HB+65. Более подробно о предельных контактных напряжениях см. практ. занятие №3. Коэффициент долговечности по контактным напряжениям в соответствии с (1.14):
KHLj = 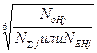 (2.12)
(2.12)
Значения базового числа циклов напряжений контактной кривой усталости NOHj лежит в диапазоне 107 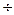 1.2*108 при изменении твердости рабочих поверхностей HB в диапазоне 350НВ…630НВ. В промежутке между указанными значениями твердости база испытаний NOHj = 30*HBj2.4. При вычислении КНLj значение суммарного числа циклов N∑j подставляется в случае постоянной нагрузки передачи, а эквивалентное – NEHj при переменной (см. лекцию №3).
1.2*108 при изменении твердости рабочих поверхностей HB в диапазоне 350НВ…630НВ. В промежутке между указанными значениями твердости база испытаний NOHj = 30*HBj2.4. При вычислении КНLj значение суммарного числа циклов N∑j подставляется в случае постоянной нагрузки передачи, а эквивалентное – NEHj при переменной (см. лекцию №3).
б) Допустимый коэффициент запаса по контактным напряжениям
[SH ], общие соображения по назначению которого изложены в л. №3, нормирован ГОСТ 21354-87. Его значения изменяются в зависимости от материалов зубчатых колес, их термической обработки, степени опасности отказа, точности назначения нагрузки и назначаются в соответствии с рекомендациями указанного стандарта.
в) Коэффициент, учитывающий конструктивно-технологические особенности проектируемой детали от образца, на котором получают опытные значения σ0Hlimb, в зубчатых передачах определяется следующим образом
КК-Т.Нj = ZRjZvZxjZсм , (2.13)
где ZRj - коэффициент, учитывающий шероховатость рабочей поверхности, который назначают по шероховатости j элемента передачи;
Zv – коэффициент, учитывающий окружную скорость;
Zxj – коэффициент масштабного фактора j элемента передачи;
Zсм – коэффициент, учитывающий влияние смазки.
Числовые значения указанных коэффициентов назначаются по рекомендациям стандарта (см. практическое занятии № 3). Таким образом,
[σн]j = 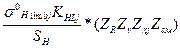 . (2.14)
. (2.14)
1.1.2.2. В расчетной модели оценки рабочих напряжений σн прежде всего отметим то обстоятельство, что эти напряжения возникают в определённый период зацепления по любой линии контакта зубьев, лежащей в пределах активной (рабочей) их поверхности. Однако практический интерес имеют напряжения σн в той зоне, где происходит контактное выкрашивание. Напомним, что выкрашивание наблюдается на ножке зуба вблизи полюсной линии. С целью упрощения расчетов σн определяют при зацеплении в полюсе.
Контактные напряжения в зубьях передачи, взаимодействующих силой Fn, моделируют сжатием двух цилиндров радиусами кривизны эвольвент в полюсе зацепления R1=ρ1 и R2=ρ2 (рис 2.9). С геометрических позиций контакт реальных зубьев и цилиндров объединяет начальный контакт по линии. Тем обстоятельством, что эвольвентные цилиндрические поверхности имеют переменные радиусы кривизны в отличие от круговых, можно пренебречь в силу малости размера hкон (рис 6.2) и плавности изменения радиуса кривизны ρ эвольвент. Далее рассмотрим возможность использования классической формулы Герца (1.23) для описания рабочих контактных напряжений с физических позиций. В этих целях сравним условия, для которых получена зависимость классической механики, с условиями работы зубчатых передач.
1.В задаче Герца цилиндры нагружены статическими сжимающими силами Fn. Поверхности зубьев, имеющих относительное перемещение, как отмечалось выше, нагружены циклически действующими силами Fn, касательной силой трения Ffr и дополнительной внутренней динамической нагрузкой, связанной с неравномерностью вращения ведомого колеса.
 Рис. 2.9. Моделирование контактных напряжений в зубьях с помощью сжатия круговых цилиндров
Рис. 2.9. Моделирование контактных напряжений в зубьях с помощью сжатия круговых цилиндров
2. Разделительная среда между сжимаемыми цилиндрами в классической задаче не предполагалась. Зубчатые колеса в большинстве случаев работают со смазкой и между зубьями возникает разделительная масляная плёнка, существенно влияющая на процесс усталостного выкрашивания.
3.Образующие сжимаемых круговых цилиндрических поверхностей принимались параллельными, а на рабочих поверхностей зубьев реальной зубчатой передачи они имеют перекос относительно друг друга из-за неточностей изготовления, перекоса и деформации валов, износа и т. п.
В общем случае для ответа на вопрос о возможности использования зависимостей классической механики или вообще зависимостей, полученных в родственных задачах, необходимо установить сколь значительно влияют на результат обнаруженные различия и при заметном влиянии найти механизмы компенсации подобных явлений. Как выше отмечено, замена сжатия двух эвольвентных цилиндрических поверхностей круговыми не вызывает серьезных изменений геометрии контакта и подобную замену принимают. Возможность перекоса образующих поверхностей контакта, а также дополнительная динамическая нагрузка могут значительно изменить величину фактических напряжений. Для компенсации этого влияния в формулу Герца вводятся коэффициенты, учитывающие неравномерность распределения нагрузки по линии контакта КНβ и дополнительную внутреннюю динамическую нагрузку Кнv. Что касается силы трения, циклического нагружения зубьев, разделительной масляной пленки, оказывающих заметное воздействия на процесс контактного выкрашивания, то их влияние учитывают при назначении допускаемых напряжений [σн]. Подобная возможность связана с тем, что предельные напряжения σ0Hlimв определяются в опыте, который проводят непосредственно на зубчатых передачах или на фрикционных катках, испытываемых с воздействием всех вышеперечисленных факторов.
Таким образом, для оценки рабочих контактных напряжений можно использовать формулу Герца для начального контакта по линии (1.23):
σн = 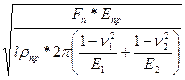
Дата добавления: 2016-10-26; просмотров: 1656;











