Силовой расчёт подшипников качения

В разделе, посвященном проектированию валов и осей, были установлены реакции в их опорах, которые и являются нагрузкой на подшипники. Задача силового расчёта подшипников качения – установление нагрузки на отдельные тела качения F₁ и закономерности их изменения во времени. Рассмотрим отмеченные вопросы для трёх случаев:

1. Подшипник упорный. Нагрузка на подшипник осевая 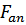(равная сумме всех внешних осевых сил 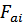, действующих на вал и, естественно, осевой реакции 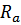, т.е. 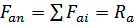) – рис 16.1a;

2. Подшипник радиально-упорный. Нагрузка – осевая 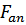– рис. 16.1б;

3. Подшипник радиальный. Нагрузка – радиальная 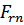(суммарная радиальная реакция в опоре ).

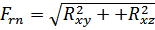1. Анализ рис. 16.1а показывает, что все тела качения упорного подшипника в случае строгого расположения силы 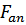по геометрической оси, отсутствии перекоса колец и искажения размеров тел качения и колец находятся в одинаковых условиях и, следовательно, сила 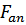в этом случае равномерно распределяется между всеми Z телами качения. Из условия равновесия всех элементов подшипника ( 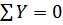) и вала очевидно

,

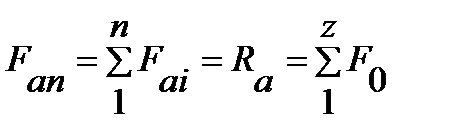где n – число элементов на валу, в которых имеют место осевые силы;

R_a – осевая реакция в опоре;

F₀ – нагрузка на одно тело качения.

Однако реальные возможности в точности изготовления элементов подшипников и опоры в целом, деформации валов и осей приводят к неравномерному нагружению тел качения, которое при повышенных требованиях к точности подшипниковых узлов, не превышает 10-20%. При вычислении силы на отдельные тела качения – F₀ этот факт можно учесть коэффициентом неравномерности распределения нагрузки – К_н=1,1…1,2

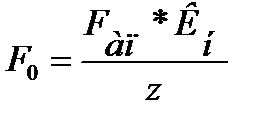. (16.1)

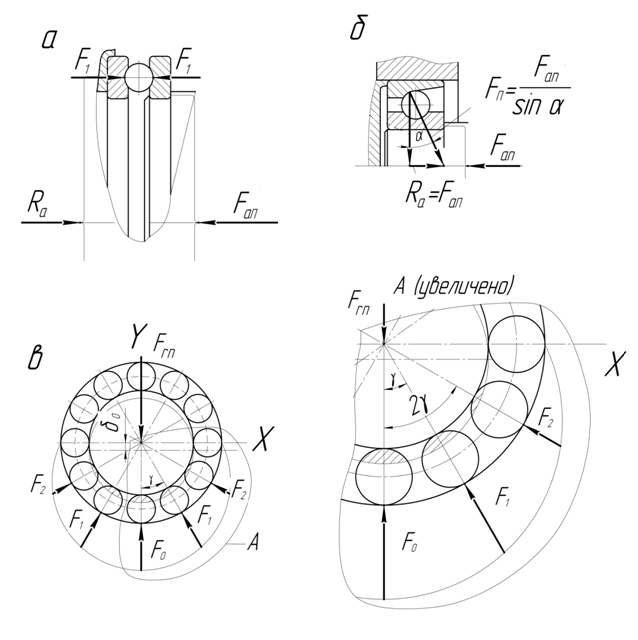
Рис 16.1. Распределение нагрузки на опору между телами качения: а – осевой F_aп – в упорном; б – осевой F_aп – в радиально-упорном; в – радиальной F_rп – в радиальном подшипниках

2. Нагрузка отдельного тела качения в радиально-упорном подшипнике при нагружении его осевой силой 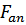определяется силой взаимодействия тела качения с кольцами, которая в случае пренебрежения силами трения, направлена по нормали к площадке контакта – F_n (рис. 16.1б). Как известно (см. лаб. раб. № 5) положение нормали в радиально-упорных подшипниках определяется углом контакта 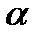. Из силового треугольника, построенного для суммарной силы F_n всех тел качения, нагрузку на один из них по аналогии с предыдущим случаем можно записать так

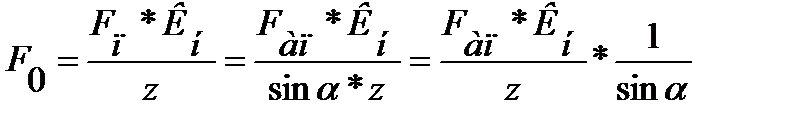. (16.2)

Известно, что для конструктивных исполнений шариковых радиально-упорных подшипников, показанных на рис.16.1б, 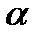=12⁰; 26⁰ и 36⁰. Тогда соответственно

F₀ 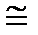(5,6; 2,3; 2,0) .

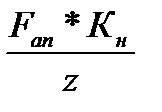Коэффициент К_н зависит от тех же факторов, что и в предыдущем случае и принимает такие же значения (К_н=1,1 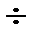1,2).

Из сравнения двух рассмотренных случаев при равной осевой силе 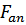нагрузка отдельных тел качения при использовании шариковых радиально-упорных подшипников в (5,6…2,0) раза выше, чем для упорных. Особо аккуратно следует отнестись к применению в данном случае радиальных подшипников, способных воспринимать незначительные двухсторонние осевые нагрузки. В них угол 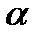<12⁰, а нагрузка отдельного шарика F₀, будет существенно превышать максимальное значение 5,6 для подшипника радиально-упорного.

3. Сила F₀ на отдельное тело качения при нагружении радиальных, а также радиально-упорных и упорно-радиальных подшипников радиальной нагрузкой F_rп (рис.16в) определяется в соответствии со следующими положениями:

Сила F_rп вполне очевидно нагружает лишь нижнюю (на рис.16.1в) половину тел качения и распределяется между 0,5Z нагруженными телами неравномерно. Неравномерность распределения нагрузки, прежде всего, определяется соотношением деформаций тел качения. При установлении закона изменения деформаций предполагают, что радиальные зазоры между телами качения и кольцами отсутствуют, а изгибные деформации колец, а также допуски на размеры силовых элементов подшипников равны нулю. С учётом этих допущений при нагружении подшипника силой F_rп ось его внутреннего кольца сместится относительно оси наружного на величину суммарной деформации 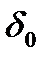колец и тела качения, находящегося в плоскости действия силы F_rп (рис 16.2а)

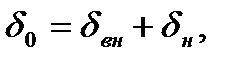
где 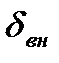и 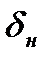– суммарные деформации колец и тела качения в месте контакта соответственно с внутренним и наружным кольцами (на рис.16.2а кольца схематично представлены окружностями дорожек качения).

Как следует из рис. 16.2б при опускании внутреннего кольца на величину 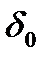тела качения, расположенные под углом 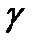, 2 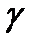, ..., n 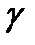по отношению к плоскости F_rп, деформируются в направлении нормали соответственно на величину:

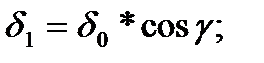
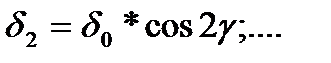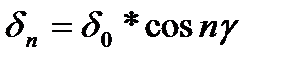; , (16.3)

где n 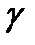- угол отклонения «n» тела качения от плоскости действия F_rп.

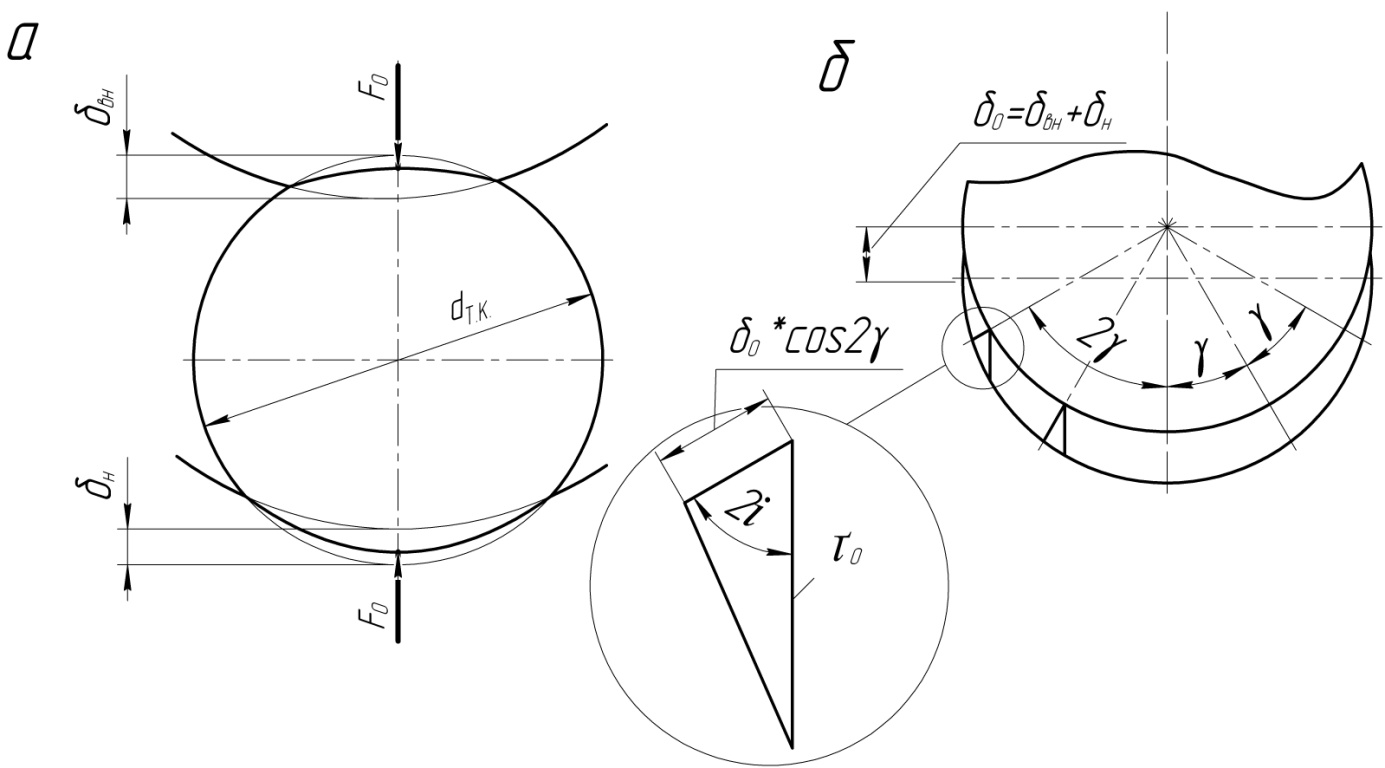
Рис 16.2 Схема деформирования колец и тел качения: a – для тела, находящегося в плоскости действия F_rп; б – для тел качения в зависимости от их положения относительно этой плоскости

Таким образом, сформулирована физическая модель закона распределения деформаций отдельных нагруженных тел качения в радиальном подшипнике, а, следовательно, в соответствии с законом Гука о пропорциональности деформации нагрузке, и закона распределения сил F₀, F₁, F₂ и т.д. Для количественной оценки отмеченных сил составим уравнения равновесия элементов подшипника. Очевидно, что в решаемой задаче возможно составить лишь одно из них – ΣZ = 0, поскольку остальные условия не имеют смысла, т.к. относительно оси Х внешняя нагрузка в рассматриваемой задаче отсутствует, а плечи сил F₀, F₁, F₂ и т.д. (относительно оси) равны нулю

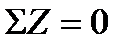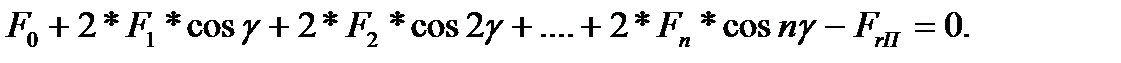; (16.4)

В единственном записанном уравнении значения F₀, F₁, F₂ и т.д. неизвестны и, следовательно, задача их определения относится к статически неопределимым. При решении подобных задач уравнения равновесия дополняют уравнениями совместности перемещений или деформаций тел качения в конкретной решаемой задаче. Уравнения совместности деформации сформулированы ранее при установлении физической модели закономерности распределения нагрузки между телами качения и имеют вид (16.3). Зависимость между силой и деформацией шарика и колец в месте контакта шарикового однорядного радиального подшипника определяется так

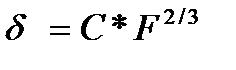, (16.5)

где С – коэффициент пропорциональности. С учетом этой зависимости уравнения (16.3) можно записать так

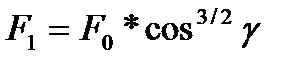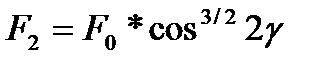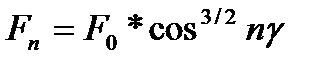, , … , (16.6)

После подстановки (16-6) в уравнения равновесия (16.4) получим

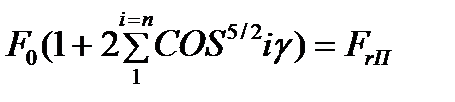(16.7)

Для получения универсальной формулы оценки F₀ в различных подшипниках домножим обе части уравнения на число тел качения z и решим уравнения относительно искомой величины F₀

,

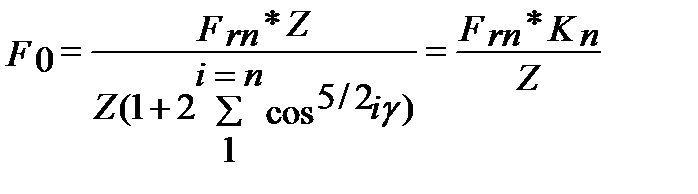где 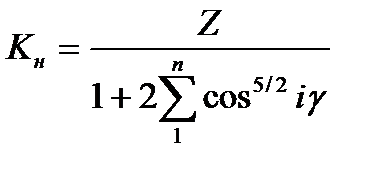. (16.8)

Значения коэффициента неравномерности распределения нагрузки между телами качения для радиальных шарикоподшипников с Z=10 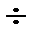20, вычисленные по (16.8), составляет 4.37 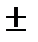0,01. С учетом зазоров между кольцами и телами качения, а также изгибных деформаций наружного кольца, устанавливаемого в посадочное отверстие с зазором, в практических расчетах принимают К_н =5.0. Аналогично решаемая задача применительно однорядных роликовых радиальных подшипников дает теоретическое значение К_н =4.0, которое в практических расчетах по названным причинам увеличивают до 4,6.