Формирование расчетных моделей валов и осей

Построение моделей включает следующие операции (рис. 3.1):

1. Рассматривают валы и оси, вращающиеся в подшипниках, как шарнирные балки (полагая размер их по длине существенно большим

диаметра), а закрепленные в корпусных деталях оси – как жестко защемленные.

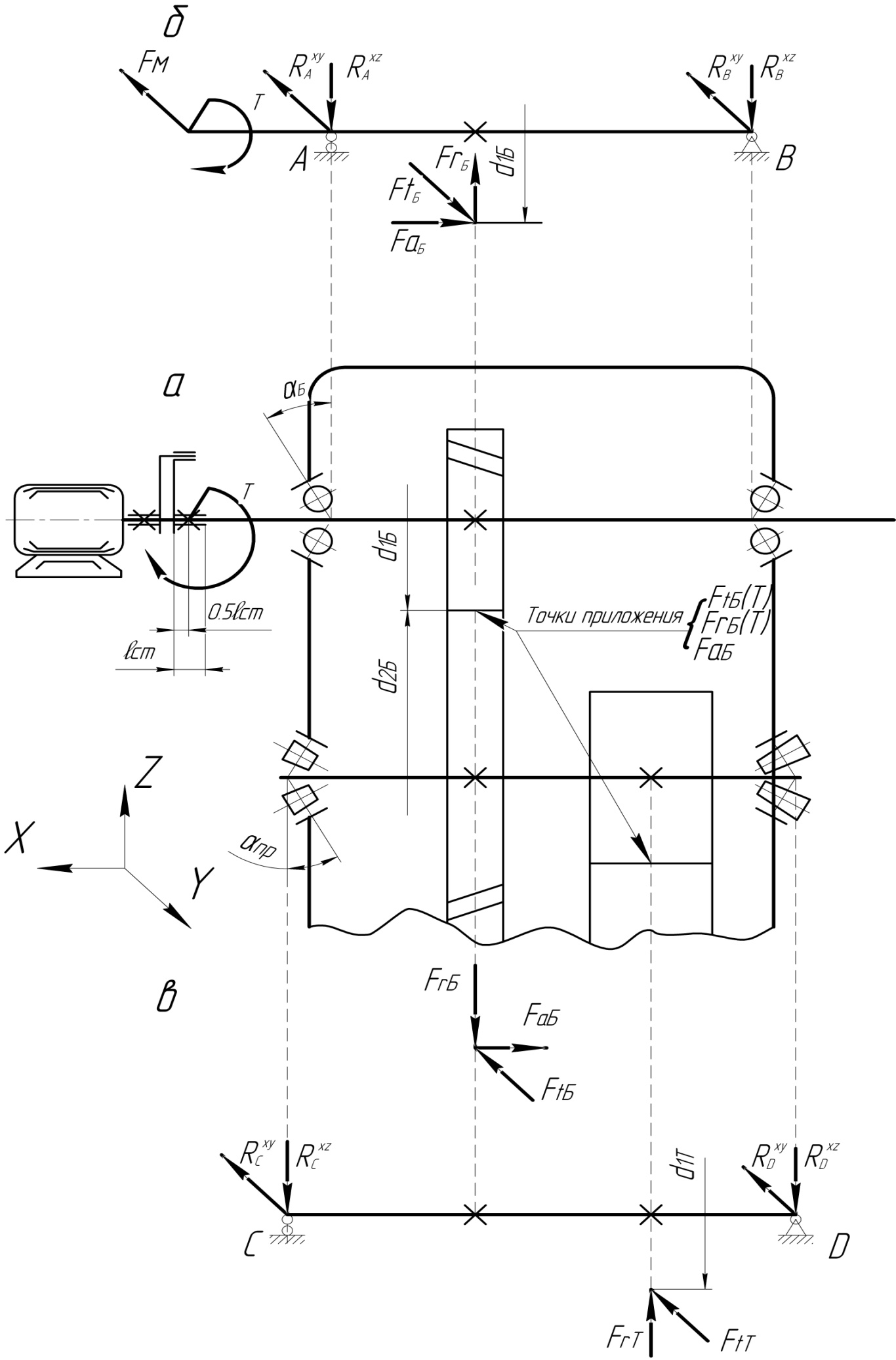Рис 3.1. Формирование расчетной модели валов: а – конструктивная схема фрагмента передаточного механизма; б – расчетная схема быстроходного вала; в – расчетная схема промежуточного вала

2. Определяют место расположения осей шарниров на балке. При решении этой задачи руководствуются следующими соображениями. Для радиальных подшипников в силу симметричности расположения тел качения в желобе колец сила их взаимодействия F (равнодействующая сил давления) проходит через ось шарика или середину ролика и ориентирована перпендикулярно оси балки (рис 3.2а). По этой причине ось шарнира располагают посередине тела качения. В радиально упорных подшипниках сила взаимодействия F наклонна к оси вала под углом контакта α и положение оси шарнира определяется точкой пересечения вектора F с осью балки (рис. 3.2б). В конструктивной схеме (рис. 3.1а) применены именно радиально-упорные подшипники и в соответствии с изложенным определено положение осей шарниров. В случае использования в опоре сдвоенных радиально-упорных подшипников обычно располагают ось шарнира в середине между подшипниками (рис. 3.2в).

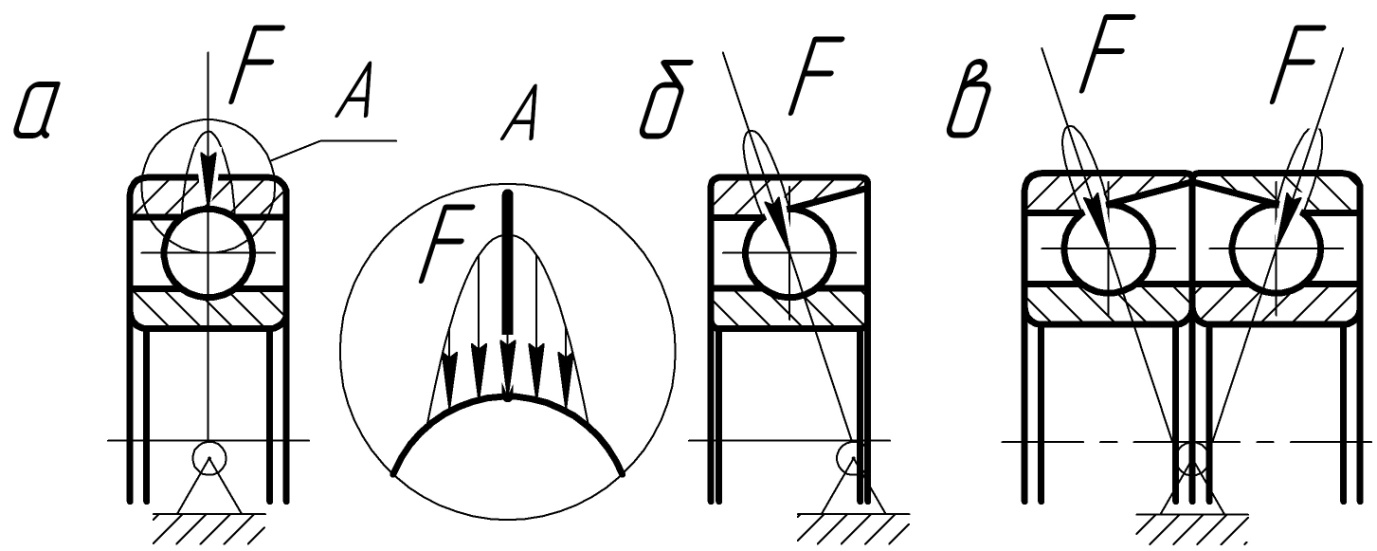
Рис. 3.2. К определению положения точек расположения осей шарниров на балке: а– в радиальных подшипниках; б – в радиально-упорных; в – в радиально-упорных сдвоенных

3. Расставляют внешние нагрузки на валы и оси и определяют реакции опор. Внешние нагрузки на вал имеют место в точках взаимодействия деталей, расположенных на валу, с контактирующими с ними деталями муфт, различных передач, кулачков и т.п. В примере на рис. 3.1. внешними силовыми элементами для быстроходного вала являются полумуфта и цилиндрическое косозубое колесо, а для промежуточного вала – зубчатые колеса.

Внешние нагрузки вала в муфтах – крутящий момент Т и радиальная сила Fм. При этом передача крутящего момента – непосредственная функция муфты, а радиальная сила является сопутствующей нагрузкой. В простейшем случае при использовании одного силового элемента, представляемого на рис. 3.3а в виде жестко закрепленного в ведущей полумуфте пальца, момент Тдв = Т передается на ведомую полумуфту посредством давления на нее этого пальца. Тангенциальная сила давления пальца на полумуфту Ft может быть определена из условия равновесия полумуфты – ΣТ=0 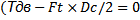). Следовательно, Ft = 2T/ Dc. Сила Ft нагружает палец и полумуфту. По отношению к валу эта сила является внецентренной и при стандартной операции приведения ее к валу она заменяется моментом и свободной радиальной силой Fм= Ft (рис.3.3а). Муфты с одним силовым элементом вследствие значительной радиальной нагрузки вала применяются сравнительно редко. В качестве примера такой муфты можно назвать предохранительную муфту со срезным штифтом. С целью снижения нагрузки на отдельные силовые элементы и радиальной нагрузки на вал используют несколько силовых элементов. Например, на рис. 3. 3б показана конструкция выше рассмотренной муфты с тремя пальцами. В подобной муфте в соответствии с уравнением равновесия окружная сила на каждый из пальцев составит

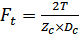. (3.2)

В случае абсолютной точности изготовления (все силовые элементы равноудалены от оси вращения, расположены на равном угловом шаге друг от друга, перекос валов и пальцев отсутствуют и т.п.) силы на каждый из пальцев Ft1 = Ft2= Ft3. При приведении Fti к оси вала силовой многоугольник является замкнутым (рис. 3.2б). В этом случае равнодействующая сил R = 0, т.е. радиальная нагрузка на вал отсутствует, а суммарный момент ТFt уравновешивает момент Тдв (рис3.2б).

Неизбежные ошибки в отмеченных выше параметрах при изготовлении и монтаже муфт приводят к тому, что приведенные к валу силы не замыкают силовой многоугольник и появляется равнодействующая R≠0 (рис.3.3в). Эта сила и нагружает вал радиальной нагрузкой Fм=R. Поскольку ошибки в изготовлении являются случайными, то и величина Fм также относится к величинам случайным. Поэтому ее рекомендуют выбирать в определенном диапазоне

Fм = (0.2 ÷ 0.5)Ft,

где меньшее значение принимают при высокой степени точности изготовления.

Далее, при корректном описании векторных величин, следует определиться с точкой приложения Т и Fм а также с направлением Fм (направление Т определено заранее). Предполагая равномерной передачу нагрузки со ступицы на вал по ее длине, можно прикладывать момент и силу посередине ступицы. Что касается направления вектора Fм, то здесь важно обратить внимание на его вращение вместе с силовыми элементами муфты. При своем вращении Fм, поворачиваясь на угол 360°, проходит положение, при котором вал находится в наиболее нагруженном состоянии. Именно это направление и следует принять для расчета вала. Определение наиболее сложного состояния вала возможно при наличии всего комплекса нагрузок вала. В связи с его отсутствием на данном этапе расчета временно не обозначаем Fм на расчетной схеме.

Влияние нагрузки на валы и оси в зубчатых и других зацеплениях определяются методами, сформулированными во втором разделе курса. Известно, что в зацеплении прямозубых колес сила взаимодействия F_n имеет тангенциальную (окружную) F_t и радиальную F_r составляющие, а в косозубых – к ним добавляется составляющая осевая F_a (см. «Силовой анализ зубчатых цилиндрических передач»). Полный комплекс составляющих (F_{t ,} F_r и F_a ) также имеют конические зубчатые, червячные и другие гиперболоидные передачи. В рассматриваемом примере (рис. 3.1.) применены цилиндрические колёса косозубые в быстроходной ступени и прямозубые – в ступени тихоходной, что и отображено в рисунке. Методы параметризации отмеченных составляющих сформулированы при изучении соответствующих типов передач. Вспомним, что модули перечисленных выше сил определяются по следующим зависимостям:

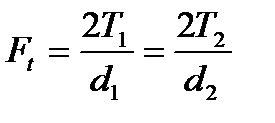, (3.3)

где – соответственно угол зацепления и угол наклона зубьев.

Точки приложения указанных сил располагают на диаметрах делительных окружностей в среднем по ширине сечениях зубчатых венцов (см. рис. 3.1). При назначении направления отмеченных сил можно руководствоваться следующими рассуждениям. Тангенциальную (окружную) составляющую F_t направляют таким образом, чтобы момент от неё создавал уравновешенное состояние вала. К примеру, на быстроходном валу передаточного механизма F_tБ является силой сопротивления движению этого вала и она направлена так, что момент 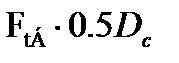уравновешивает движущий момент. На промежуточном валу F_tБ естественно будет иметь противоположное направление и на радиусе делительной окружности колеса 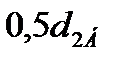будет образовывать движущий момент, приводящий промежуточный вал в движение. Окружная составляющая F_tT , приложенная к зубу шестерни тихоходной ступени, образует момент сопротивления, который уравновешивает момент движущий. Радиальные составляющие направляют по радиусу к оси вращения рассматриваемого зубчатого колеса. Для назначения направления осевых составляющих F_а проще всего использовать такое правило. Их направляют к рабочей поверхности зуба. В выделенном на быстроходной шестерне зубе при заданном направлении вращения рабочей поверхностью будет нижняя (по отношению к рисунку) грань. Именно к ней и направлена F_aБ.

После расстановки всех внешних сил на быстроходном валу следует вернуться к определению направления вектора F_М , вращающегося вместе с муфтой. Очевидно, что наиболее опасное положение вал будет иметь в случае нахождения F_М в плоскости действия максимальной из сил. В рассматриваемой задаче такой силой является F_tБ. При этом наиболее опасным для вала быстроходного будет направление F_М , противоположное силе F_tБ. При таком направлении F_М и F_tБ очевидно упругая ось вала будет наиболее деформирована и потому, в соответствии с законом Гука, будет соответствовать, наиболее нагруженному состоянию вала. Здесь важно также подчеркнуть то обстоятельство, что для опор более опасным будет направление F_М совпадающее с силой F_tБ и, следовательно, его надо принять при расчете подшипников.

Для оценки работоспособности вала также важно определить место положения шарнирно-неподвижной и подвижной опор. Как известно из лабораторной работы №5 их расположение зависит от направления осевой силы, нагружающей вал, способа установки подшипников на валу и конструкции опор. На рис. 3.1. положение опор определено в соответствии с положениями, сформулированными в лабораторной работе.

После расстановки внешних сил определяют реакции опор. Их определение проводят в соответствии с правилами, выработанными при изучении теоретической механики и сопротивления материалов. Исходными положениями для определения реакций опор являются условия равновесия вала. Для установления реакций опор удобно использовать сумму моментов относительно каждой из опор, а проверку правильности их определения проводят по суммам проекций на соответствующие оси.

Лекция № 15. Тема «Проектирование валов и осей» (продолжение)

4. Исследование загруженности вала по длине. Установление возможных опасных сечений

Основными инструментами исследования загруженности вала по длине являются эпюры нагрузки. При построении эпюр, во-первых, следует помнить о наличии в циклограммах в большинстве случаев как длительно действующих нагрузок, так и кратковременных перегрузок, во-вторых, о комплексности действующих сил и моментов, в-третьих – о действии силовых факторов в нескольких плоскостях. Построение эпюр осуществляется методами, изученными в курсе «Сопротивление материалов». С целью повторения известных положений приведем в качестве примера построение эпюр для первичного быстроходного вала, расчетная модель которого создана выше (рис.3.1).

В рассматриваемом примере фиксированные силы и изгибающие моменты нагружают вал в плоскостях XY (плоскости, перпендикулярной плоскости рисунка) и XZ (плоскости рисунка) (рис.3.3). Нефиксируемая вращающаяся сила Fм создает момент, который изгибает вал во всех сечениях вала в пределах его поворота на угол 360˚. Как отмечалось выше, из всех возможных положений изгибающего момента выбирают наиболее опасное, когда он находится в плоскости силы 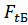. В соответствии с изложенным выше рассмотрена загруженность вала в двух плоскостях: XY и XZ.

При исследовании загруженности вала в плоскости XY, прежде всего выделим крутящий момент Т, который нагружает вал по всему поперечному сечению. Но, так как уравновешивает его момент 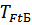, создаваемый силой 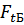, то будем рассматривать его в названной плоскости. В первую очередь изучим изменение крутящего момента по длине вала. Удобнее начинать построение эпюр вала с его торцов. К левому торцу вала с помощью шпонки (шлиц и т.д.) от ведущей полумуфты подводится момент Т. Очевидно, что с перемещением текущей координаты х от торца вправо значение Т остается неизменным. Можно так же считать величину Т неизменной при прохождении левой опоры, так как моментом трения в опоре в силу его малости обычно пренебрегают без заметной погрешности, а момент от реакции 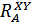= 0. Неизменным остается Т до середины шестерни. В этом сечении момент 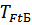полностью уравновешивает движущий момент Т (пренебрегая моментом трения в правой опоре). В периоды перегрузки вала при неустановившемся движении выделенный участок вала будет нагружен моментом 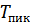, что и отражено в эпюрах крутящего момента. Величина момента 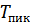как и для зубчатых передач определяется коэффициентом перегрузки –

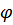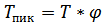
Эпюру изгибающего момента в плоскости XY также строим с левого торца вала. Очевидно, что уравнение моментов на участках: СА будет иметь вид 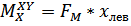; АD – 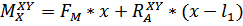, т.е. уравнений прямых линий. На участке DB это уравнение можно также представить в виде суммы моментов всех сил слева:

.

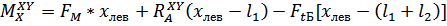Однако на этом участке проще составить уравнение в виде суммы моментов всех сил справа 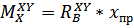. Если реакции опор определены верно, то суммы моментов сил справа и слева для любой точки должны быть равными. Исключения составляет случай приложения в данной точке сосредоточенного момента, при котором между суммой моментов сил слева и справа имеет место скачок, равный этому сосредоточенному моменту (см. эпюры М в плоскости XZ). В силу пропорциональности реакций опор и изгибающих моментов крутящему моменту Т, то ординаты эпюры 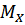при кратковременных перегрузках 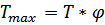в любой точке по длине вала можно определить по соотношению .

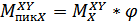В плоскости XZ (плоскости рисунка ) вал нагружают силы 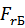и 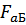с соответствующими реакциями 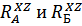. Поскольку участок СА не имеет нагрузки, то эпюра моментов начнется с опоры А. Очевидно, уравнение моментов для участка АD будет иметь вид уравнения прямой линии 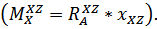В точке D осевая составляющая создает сосредоточенный момент 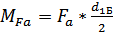. По направлению действия он совпадает с моментом от 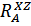, потому их следует суммировать, т.е. в точке D будет иметь место момент 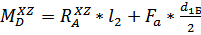. На участке DB, как и в плоскости XY более простой вид уравнения 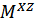будет иметь место, если рассматривать сумму моментов справа 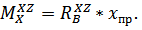Проверкой правильности определения реакций в опорах и построения эпюр будет равенство суммы моментов справа и слева для выделенного сечения. Абсолютно так же, как и в плоскости XY получим ординаты эпюры 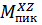при пиковой перегрузке .

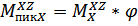Суммарный изгибающий момент в любом поперечном сечении вала получают геометрическим суммированием моментов в плоскостях действия нагрузок.

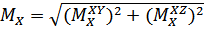; (3.4)

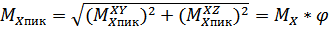(3.5)

Наконец, отметим, что участок DB подвержен сжатию силой 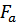и уравновешивающей ее реакцией 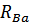. Эпюра сжимающих сил также приведена на рисунке. На заключительном этапе исследования загрузки вала по длине выделяют возможные его опасные сечения. При их назначении принимают во внимание не только эпюры нагрузки, но и геометрические параметры сечений и их конструктивные особенности. В качестве возможных опасных сечений для проверки прочности валов, если они не могут быть установлены аналитически, естественно принять: Сечения с максимальной нагрузкой;

Сечения с минимальными размерами нагруженные;

Сечения со значительной нагрузкой и концентрацией напряжений.

5. Проверочный расчет валов на прочность

В соответствии со сказанным выше и построенными эпюрами в нагрузочном спектре валов чаще имеют место как длительно действующие нагрузки, так и кратковременные перегрузки, вызывающие циклические изменения рабочих напряжений. Следовательно, валы необходимо проверить как на прочность усталостную (выносливость), так и квазистатическую. В первом разделе, посвященном общеметодическим вопросам расчетов на прочность, отмечено существование двух форм расчетов: по номинальным напряжениям (1.8) и коэффициенту запаса прочности S (1.9) В проверочных расчетах валов предпочтительнее расчет по коэффициенту S. В соответствии с (1.9)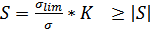

Рис.3.4. Исследование загруженности вала по длине

Из этой зависимости следует, что для оценки значения S необходимо определение предельных и рабочих 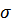напряжений. Еще раз акцентируем внимание на взаимозависимости отмеченных параметров и прежде всего, выделим зависимость от закона изменения рабочих напряжений во времени. Далее подчеркнем тот факт, что в сечениях вала действуют нормальные и касательные напряжения. В соответствии с этим сначала отдельно определяют коэффициенты запаса по нормальным и касательным напряжениям, а затем его общее значение.