Решение дифференциальных уравнений на примере RLC- цепей

Решения дифференциального уравнения на примере RL-цепи.Схема коммутации RL-цепи на источник постоянного напряжения представлена на рис. 2.40.

Рис. 2.41. Схема коммутации RL -цепи на источник постоянного напряжения

Процессы, протекающие в цепи при замыкании ключа, описываются дифференциальным уравнением 1-го порядка, составленным по второму закону Кирхгофа:

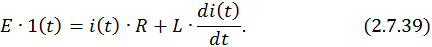
Характеристическое уравнение получается из однородного ДУ для переменной 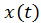путем его алгебраизации, которая заключается в замене оператора дифференцирования на переменную 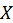. При этом степени новых переменных 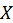равны порядку соответствующих производных. После алгебраизации переменная 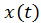выносится за скобки, а полином, находящийся в скобках, после приравнивания его к нулю будет представлять собой характеристическое уравнение.

Однородное дифференциальное уравнение –

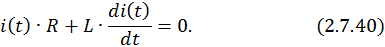
Определим корень характеристического уравнения –

Общее решение i₀(t) однородного уравнения –

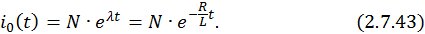
Для нахождения частного решения неоднородного ДУ подставим в исходное уравнение значение t = ∞. Тогда оно будет выглядеть следующим образом:

Общее решение неоднородного уравнения –

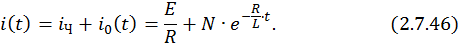
Решим задачу Коши с нулевыми начальными условиями. Для этого подставим в общее решение неоднородного ДУ значение 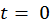. Получим

откуда постоянная интегрирования

В итоге временная зависимость тока в RL -цепи при коммутации ее на источник постоянного напряжения

Графическое решение ДУ представлено на рис. 2.42:

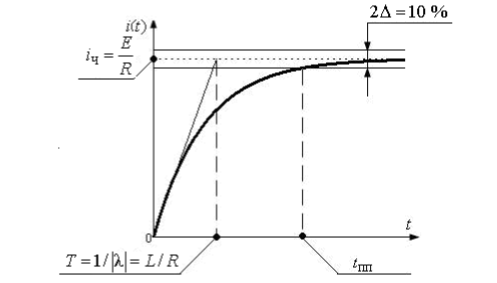
Рис. 2.42. Изменение тока в RL-цепи при коммутации на источниках постоянного напряжения

На графике обозначена также постоянная времени цепи Т, обратная модулю корня характеристического уравнения .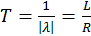

Решения дифференциального уравнения на примере RС-цепи.Схема коммутации RC-цепи на источник постоянного напряжения представлена на рис. 2.43.

Рис. 2.43. Схема коммутации RC-цепи на источник постоянного напряжения Е

Дифференциальное уравнение, составленное по второму закону Кирхгофа, описывает процессы в цепи после замыкания ключа:

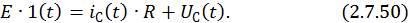
Учитывая, что 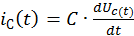,это уравнение можно записать в следующем виде:

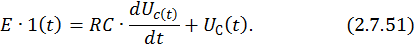
Найдем общее решение однородного уравнения:

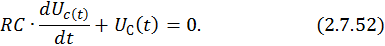
Определим корень характеристического уравнения:

Общее решение 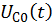однородного дифференциального уравнения:

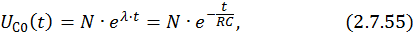
Для нахождения частного решения неоднородного ДУ подставим в исходное уравнение значение t =∞. Тогда оно будет выглядеть следующим образом:

Общее решение неоднородного уравнения –

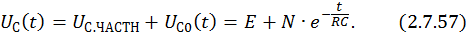
Решим задачу Коши с нулевыми начальными условиями. Для этого подставим в общее решение неоднородного ДУ значение t = 0. Получим

откуда постоянная интегрирования

В итоге временная зависимость тока в RC-цепи при коммутации ее на источник постоянного напряжения

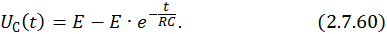
Графическая зависимость напряжения на конденсаторе от времени представлена на рис. 2.44.

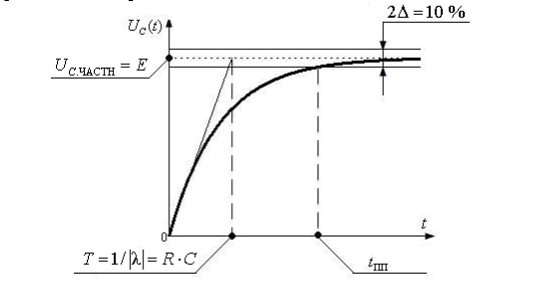
Рис. 2.44. Изменение напряжения на конденсаторе при коммутации на источник постоянного напряжения

На графике обозначена также постоянная времени цепи Т, обратная модулю корня характеристического уравнения .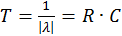

Решения системы дифференциальных уравнений на примере RLC-цепи.Коммутация RLC-цепи на источник постоянного напряжения представлена на рис. 2.45.

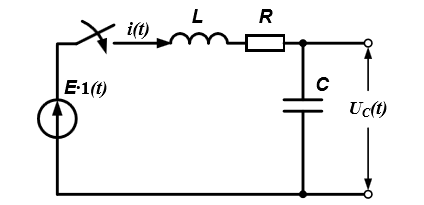
Рис. 2.45. Схема коммутации RLC-цепи на источник постоянного напряжения

Составим СДУ по первому и второму законам Кирхгофа:

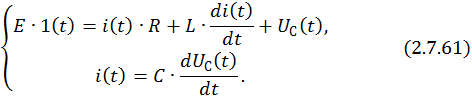
Представим СДУ в нормальной форме Коши:

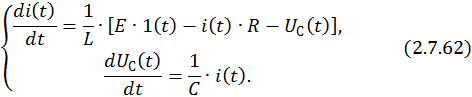
Запишем СДУ в матричной форме:

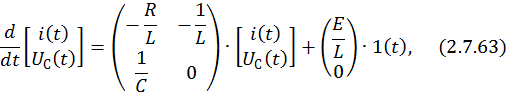
где 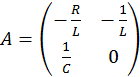- матрица коэффициентов перед переменными состояния RLC-цепи; 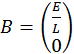– вектор свободных членов СДУ; 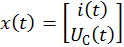–вектор переменных состояний RLC-цепи.

Однородная СДУ, соответствующая неоднородной СДУ, –

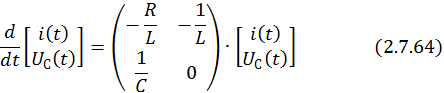
Найдем собственные значения матрицы A, составив характеристическое уравнение 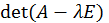=0:

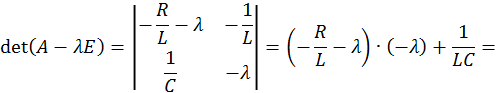
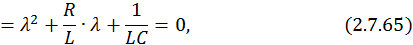
Это уравнение вида λ² + а λ + b = 0 имеет следующее решение:

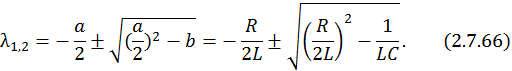
Предположим, что корни характеристического уравнения действительные, различные: λ₁ = –a, λ₂ = –b, где a и b – неотрицательные числа. Отметим также, что для устойчивости динамической системы необходимо, чтобы действительные части корней характеристического уравнения были отрицательными.

Найдем собственные вектора для каждого собственного значения матрицы A. Для значения λ₁ = –a алгебраическая система уравнений будет выглядеть следующим образом:

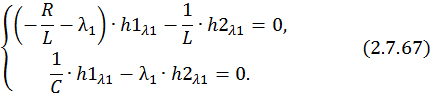
или

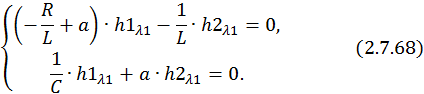
Примем значение 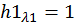и определим 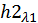из второго уравнения системы:

Собственный вектор для первого собственного значения матрицы A –

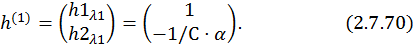
Аналогично будет находиться собственный вектор и для второго собственного значения матрицы A:

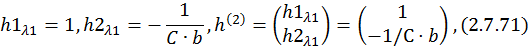
Общее решение СДУ 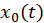запишется в виде

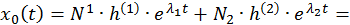
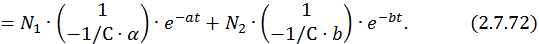
Можно записать отдельно выражения для каждой временной функции:

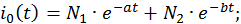
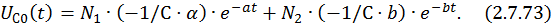
Предположим, что корни характеристического уравнения комплексно сопряженные: λ_1,2 = –α ± jβ, где α и β – неотрицательные числа. В этом случае собственный вектор ищется только для одного из этих значений.

Найдем собственный вектор для λ₁ = –α + jβ:

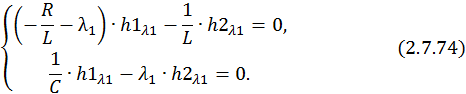
Принимаем 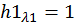и находим 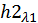из второго уравнения системы:

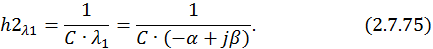
Общее решение однородной СДУ в этом случае запишется в виде

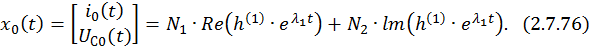
Запишем каждую компоненту общего решения отдельно:

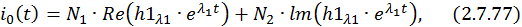
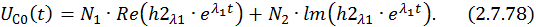
Найдем составляющие общего решения однородной СДУ. По формуле Эйлера для комплексных чисел

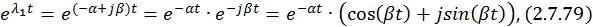
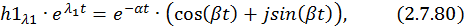
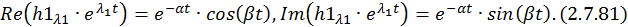
Для разделения вещественной и мнимой частей второй составляющей 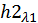собственного вектора домножим числитель и знаменатель 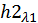на число, комплексно сопряженное знаменателю :

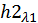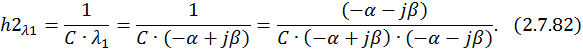
Учитывая формулу умножения комплексно сопряженных чисел друг на друга, запишем:

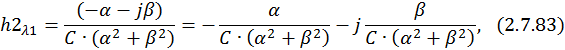
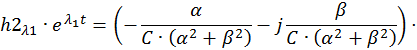
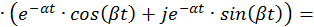
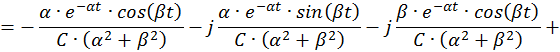
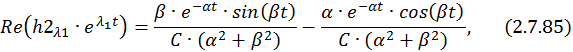
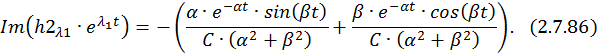
Общее решение однородной СДУ:

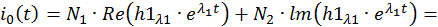
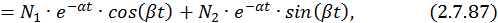
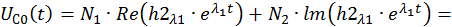
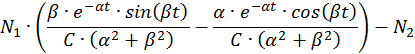
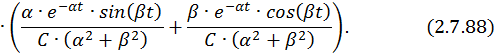
Как видно, при действительных корнях общее решение однородной СДУ включает в себя только экспоненты, а при комплексно сопряженных корнях еще и синусные и косинусные составляющие. В первом случае переходные процессы в ЭМС имеют апериодический характер, а во втором случае – затухающий колебательный.

Найдем частное решение неоднородной СДУ при подстановке в исходную СДУ значения :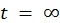

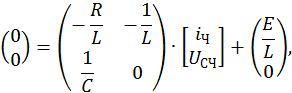
или

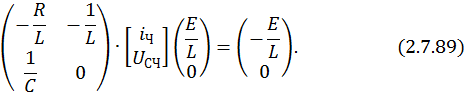
Найдем решение этой СЛАУ методом Крамера:

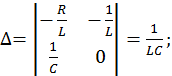
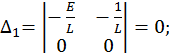
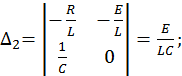
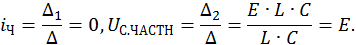
Полученное частное решение неоднородной СДУ легко объясняется физически – конденсатор заряжается до напряжения источника питания E, а ток в цепи после окончания переходного процесса становится равным нулю, так как при работе на постоянном токе конденсатор представляет собой разрыв цепи.

Следующим этапом является нахождение постоянных времени путем подстановки в общее решение неоднородной СДУ значения t = 0 и последующего решения получившейся СЛАУ. Решим задачу Коши для обоих случаев собственных значений матрицы A – действительных и комплексно-сопряженных.

Найдем постоянные интегрирования при действительных отрицательных собственных значениях матрицы A: λ₁ = –a, λ₂ = –b. Общее решение неоднородной СДУ в этом случае имеет вид

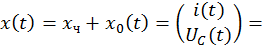
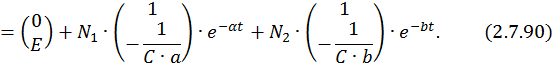
Подставим в это выражение значение времени 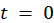. Так как начальные условия нулевые, то 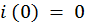, 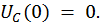Также экспоненты в нулевой степени обращаются в единицу. Запишем получившуюся СЛАУ:

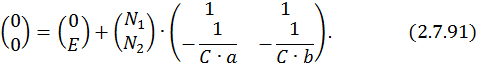
Перенесем свободные члены:

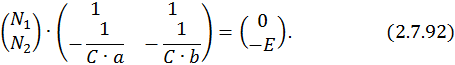
Решим эту СЛАУ методом Крамера:

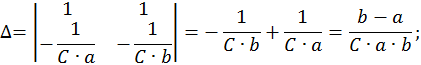
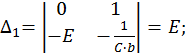
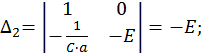
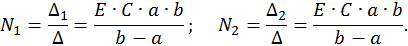
Запишем компоненты общего решения неоднородной СДУ:

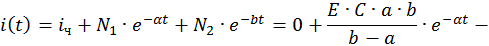
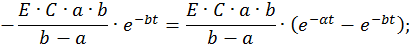
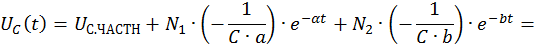
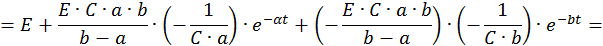
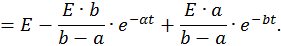
Определим постоянные интегрирования при комплексно–сопряженных корнях характеристического уравнения: λ_1,2 = –α ± jβ. Общее решение неоднородной СДУ имеет в этом случае следующий вид:

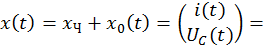
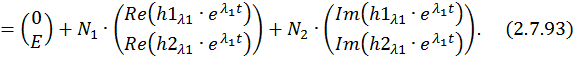
Подставим в это выражение значение времени 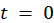. Учитывая нулевые начальные условия, запишем получившуюся СЛАУ:

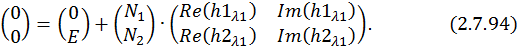
Перенесем свободные члены, а также учтем, что 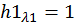и , :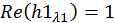

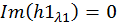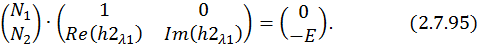
Решим эту СЛАУ методом Крамера:

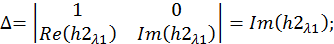
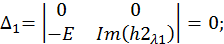
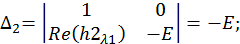
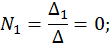
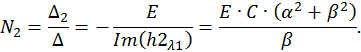
Запишем компоненты общего решения СДУ:

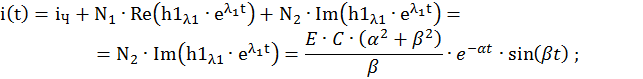
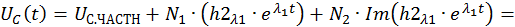
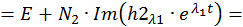
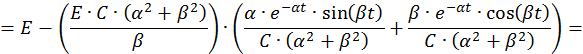
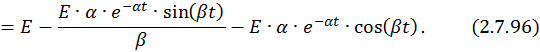
Графические решения СДУ при разных случаях корней характеристического уравнения показаны на рис. 2.46 и 2.47 соответственно.

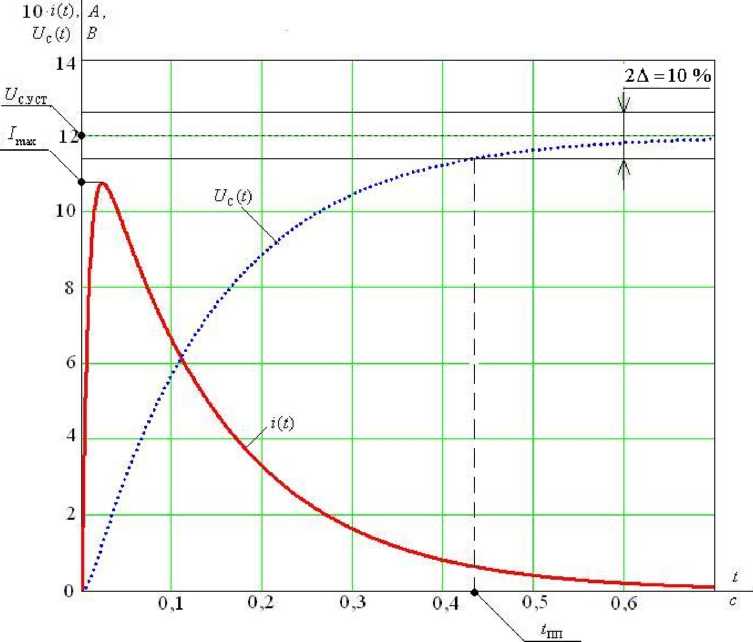
Рис. 2.46.Переходные процессы в RLC-цепи при действительных корнях характеристического уравнения

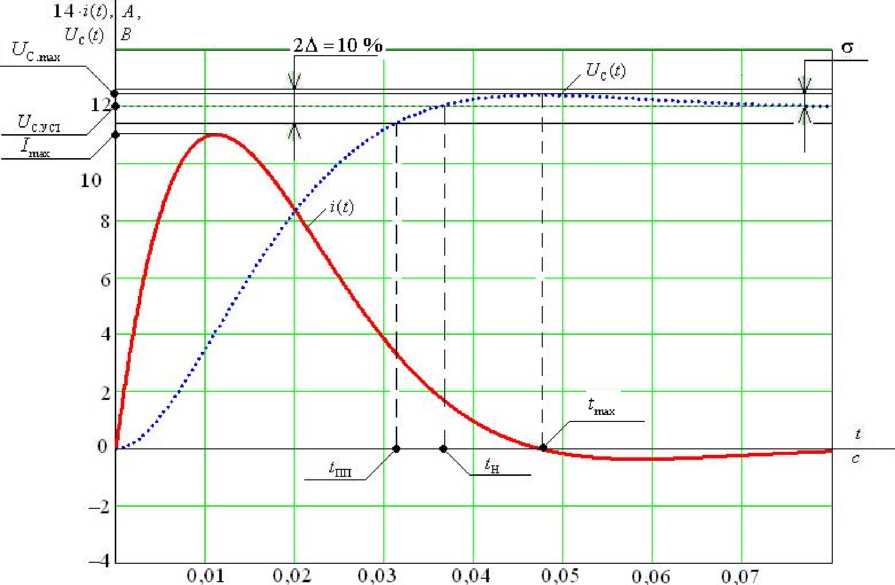
Рис. 2.47.Переходные процессы в RLC-цепи при комплексно-сопряженных корнях характеристического уравнения