Пример 2.15. Проверка электродвигателя по тепловому режиму при повторно-кратковременном режиме работы

При повторно-кратковременном режиме работы мощность выбранного двигателя по условиям нагревания проверяется по соотношению

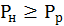
где Р_р – расчетная мощность электродвигателя, определяется по формуле

.

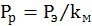
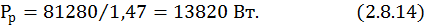Среднеэквивалентная мощность нагрузки

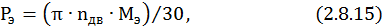
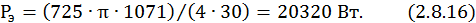
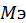– среднеэквивалентный момент, значение взято из пункта 3 для одного двигателя.

При расчете коэффициента тепловой перегрузки учитывается и время пуска, т.е.

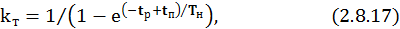
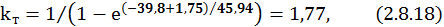
где t_П, t_p –продолжительность пуска электродвигателя, работы и паузы ;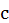

,

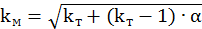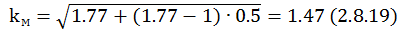
Постоянная времени Т_н рассчитывается по формуле

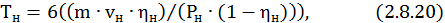
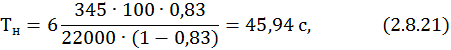
где 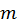– масса выбранного электродвигателя, MTF 412–8 – 345 кг; υ_н– номинальное превышение температуры обмотки статора электродвигателя. Для класса изоляции F – υ_н =100°С.

Вывод: выбранный электродвигатель удовлетворяет условиям теплового режима при работе и при пуске.

Задание 9. Расчет энергетических характеристик

Электропривода

Определение мощности потребляемой из сети и cos φ.Активная, реактивная и полная мощности, потребляемые электродвигателем из сети, определяются по известным формулам с учетом коэффициента загрузки. Для определения КПД η_З и cosφ_З электродвигателя по каталожным данным строятся графики cosφ(k)_З и η(k_З). Здесь k_З – коэффициент загрузки двигателя:

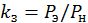. (2.9.1)

Максимальная активная мощность, 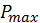, кВт:

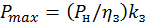. (2.9.2)

Максимальная полная мощность, 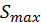, кВА:

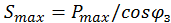. (2.9.3)

Максимальная реактивная мощность, 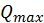, кВАр:

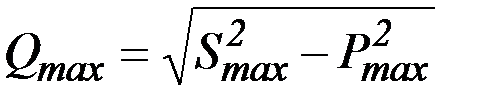. (2.9.4)

Если в каталоге в технических данных электродвигателей не приводятся значения η_З и cosφ_З при равных коэффициентах загрузки, то они определяются аналитически.

Коэффициент полезного действия η_З рассчитывается по формуле, приведенной в задании 3.

Коэффициент мощности cosφ рассчитывается по формуле

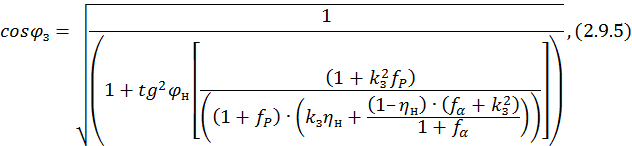
где f_p – коэффициент формы кривой cosφ:

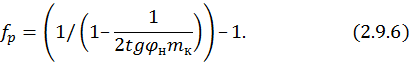
Пример 2.16.Асинхронный двигатель типа МТКН 412-6 имеет паспортные данные P_ном = 36 кВт при продолжительности включения ПВ = 25%, п_ном = 920 об/мин; I_1ном = 81 А, I _μ = I _1х.х = 41,5 A; R₁ = 0,13 Ом; х₁ = 0,2 Ом; R₂^/ = 0,24 Ом; х₂^/ = 0,25 Ом.

Определить коэффициент мощности при его работе на естественной характери­стике с моментом нагрузки М = 0.5М_ном.

Решение. Расчет cosφ производится по формуле, для чего предварительно опре­делим скорости в режимах идеального холостого хода и при номинальной на­грузке двигателя:

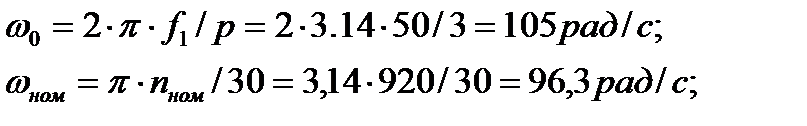(2.9.7)

номинальные скольжение и момент двигателя:

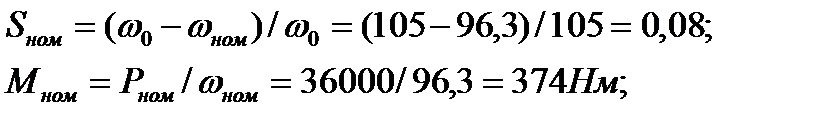(2.9.8)

скольжение на естественной характеристике, соответствующее моменту нагрузки:

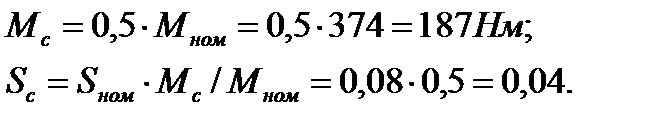(2.9.9)

Определим приведенный ток в роторе АД при моменте на­грузки

М = 187 Н·м.

Найдем номинальную активную потребляемую мощность из сети:

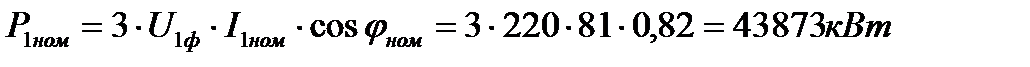(2.9.10)

Вычислим полные номинальные потери мощности:

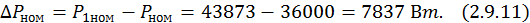
Найдем номинальный приведенный ток ротора.

Постоянные потери мощности:

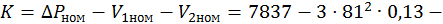
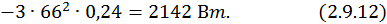
Потребляемая активная мощность при заданном моменте нагрузки:

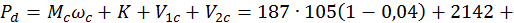
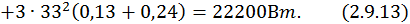
Реактивная мощность:

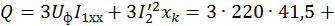
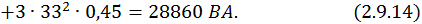
Искомый коэффициент мощности при работе АД в заданной точке:

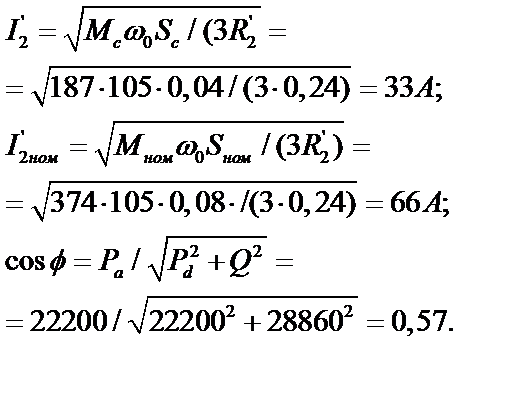(2.9.15)

Пример 2.17. Расчет мощности и cosφ, потребляемые из сети двигателем

Коэффициент загрузки двигателя определяется по формуле

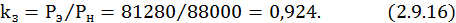
Максимальная активная мощность

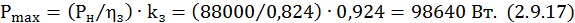
Максимальная полная мощность

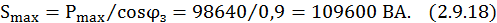
Максимальная реактивная мощность

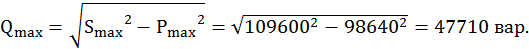
Коэффициент полезного действия η_з рассчитывается по формуле

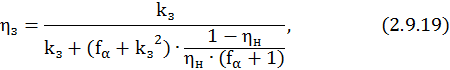
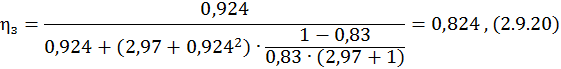
где f_a – коэффициент формы кривой КПД.

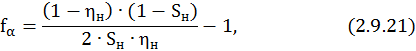
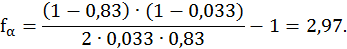
Коэффициент мощности cosφ_з рассчитывается по формуле:

где f_p – коэффициент формы кривой cosφ

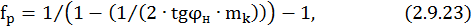
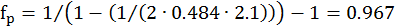
где m_k – максимальный момент, m_k=2.1.

Вывод: Коэффициент мощности имеет высокое значение (cosφ_з=0,9). Это объясняется тем, что двигатели работают с высоким коэффициентом загрузки (0,924), поэтому потребляют из сети очень малое количество реактивной энергии.